сетевые модели. СЕТЕВЫЕ МОДЕЛИ. Сетевые модели

• Название: Сетевые модели
• Анкор: сетевые модели
• Дата: 26.03.2023
• Размер: 159.5 Kb.
• Имя файла: СЕТЕВЫЕ МОДЕЛИ.doc
• Тип: Документы; #1015077

СЕТЕВЫЕ МОДЕЛИ
Сетевые модели являются основным мощным и гибким организационным инструментом управления. Они позволяют осуществлять календарное планирование работ, оптимизацию использования ресурсов, сокращать продолжительность выполнения работ в зависимости от стоимости работ или же увеличивать продолжительность исходя из бюджетных ограничений, организовывать оперативное управление и контроль в ходе реализации деятельности.

Сетевая модель представляет собой ориентированный граф (геометрическую фигуру, состоящую из вершин и направленных стрелок), изображающий все необходимые для достижения цели проекта операции показаны в технологической взаимосвязи.

Основными понятиями сетевой модели являются:

• 
  Работа,
  
• 
  Событие,
  
• 
  Путь.
  

Работа – это трудовой процесс, требующий затрат времени и ресурсов. В модели работа изображается в виде сплошной стрелки (дуги графа), над которой стоит цифра, показывающая ее продолжительность. Работа идентифицируется номерами начального и конечного события. Иногда в более сложных сетевых моделях допускается нанесение (сверху или снизу от стрелки) и других условных изображений, таких как наименование работы, стоимость работы, объем работ, исполнителя, продолжительности, количества ресурсов. С другой стороны иногда используются модели без каких-либо числовых показателей и обозначений. Такая сеть называется структурной сетевой моделью, или топологией.

В понятие работа включается «процесс ожидания», т.е. процесс, не требующий затрат труда, но требующий затрат времени. Обычно ожидание изображают в виде пунктирной стрелки, над которой изображают продолжительность ожидания

В понятие работа также включается «зависимость» между двумя или несколькими событиями, не требующая ни затрат времени, ни ресурсов, но показывающая логическую связь работ, например, что начало одной или нескольких работ зависит от результатов другой работы. В модели эта зависимость (или как часто ее не совсем правильно называют «фиктивная работа») показывается в виде пунктирной стрелки без указания времени.

Зависимость используется в сетевых моделях не только как технологическая или организационная связь, но и как элемент, необходимый для выполнения определенных правил построения сетевых моделей.

Событие – это результат выполнения одной или нескольких работ, позволяющий начинать другую работу. В сетевых моделях событие изображается, как правило, в виде кружка.

События не являются процессом и не имеют длительности, т.е. совершаются мгновенно. Поэтому каждое событие, включаемое в модель, должно быть полно, точно и всесторонне определено (с точки зрения логической связи работ), его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ (ни больше, ни меньше).

Событие, стоящее в начале сетевой модели, в которое не входит ни одной работы, называется исходным событием сети. Событие, стоящее в конце сетевой модели, из которого не выходит ни одной работы, называется завершающим событием сети.

События делятся на простые и сложные. Простые события это те, в которые входит одна работа. Сложные события это те, в которые входят две или более работ.

Событие может являться частным результатом отдельной работы или же суммарным результатом нескольких работ. Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие. Путь – это непрерывная последовательность стрелок, начиная от исходного события сетевой модели и заканчивая завершающим. Длина пути определяется продолжительностью работ, лежащим на этом пути.

При сравнении продолжительности путей определяется путь, длина которого (суммарная продолжительность работ на этом пути) имеет наибольшую величину по сравнению с длиной любого другого пути. Такой путь называется критическим. Критический путь определяет общую продолжительность проекта.

Правила построения сетевых моделей

Единой принятой последовательности составления сетевой модели (сетевого графика) нет. Поэтому строить графики можно по-разному – от начала проекта и до окончания, а также и наоборот – от конца к началу. Более логичным и правильным следует признать метод построения графиков от исходного события до завершающего, т.е. слева направо, так как при таком построении четко понимается технология выполнения моделируемых работ. Этот метод получил наибольшее признание.

Поэтому в качестве первого правила последовательности отображения работ следует указать, что сетевые модели следует строить от начала к окончанию, т.е. слева направо.

Правило изображения стрелок. Стрелки, изображающие работы, ожидания или зависимости, могут иметь различный наклон и длину, но должны, как правило, идти слева направо. Стрелки в сетевом графике не должны отклоняться влево от оси ординат. И конечно, следует иметь ввиду, что стрелки направляются всегда от предшествующих событий к последующим, т.е. от событий с меньшими номерами к событиям с большими номерами.

Правило пересечения стрелок. Пересечения стрелок допустимы, но чем меньше пересечений, тем нагляднее становится график.

Изложенные три правила можно рассматривать как предварительные. Теперь же перейдем к основным правилам построения сетевым графиков.

Правило обозначения работ. В практике зачастую встречаются случаи, когда две и более работ выходит из одного и того же события, выполняются параллельно и заканчиваются одним и тем же событием.

Например, одновременно начинается проектирование двух вариантов конструкции новой машины. После их разработки проводится сопоставление и выбор лучшего варианта.

Но правильное изображение этих работа на сетевом графике не должно выводить две работы из одного события и завершать их одним тем же событием. При таком изображении две работы получают одно и то же обозначение, а это недопустимо, так как при расчете сети невозможно будет определить параметры этих работ, да и всего сетевого графика.

Правило расчленения и запараллеливания работ. Во многих процессах позволяется начинать следующую работу, не ожидая полного окончания предшествующей. В этом случае производится «расчленение» предшествующей работы.
Аналитические параметры сетевых графиков

Сетевые модели представляют собой графо-аналитические организационные инструменты. Рассмотрев графическую часть этих моделей, перейдем к рассмотрению аналитических параметров.

Аналитические параметры сетевых моделей представлены в таблице 8.

Таблица 8

Аналитические параметры сетевых моделей

№	Название параметра	Условное обозначение
1	Код данной работы	i–j
2	Код начального события данной работы	i
3	Код конечного события данной работы	j
4	Код работы, предшествующей данной	h-i
5	Код события, предшествующего работе h – j	h
6	Код работы, последующей за конечным событием данной работы	j-k
7	Код события, последующего работе j – k	k
8	Путь	L
9	Продолжительность пути	TL
10	Критический путь	Lкр
11	Продолжительность критического пути	TLкр
12	Продолжительность данной работы	ti-j
13	Раннее начало данной работы	Tрнi-j
14	Раннее окончание данной работы	Tроi-j
15	Позднее начало данной работы	Tпнi-j
16	Позднее окончание данной работы	Tпоi-j
17	Общий (полный) резерв времени данной работы	Ri-j
18	Частный (свободный) резерв времени данной работы	ri-j
19	Резерв времени пути	RL

Прежде всего, определяются ранние сроки начала (T^рн_i-j) и окончания (T^ро_i-j) каждой работы. Далее – поздние сроки начала (T^пн_i-j) и окончания (T^по_i-j) каждой работы. Затем определяются критические работы, а для некритических работ – резервы времени (R_i-j,r_i-j). И, наконец, определяется так называемый коэффициент напряженности каждой работы (К_i-j).

Ранние сроки начала и окончания работ сетевой модели определяют последовательно, слева направо по графику, т.е. от исходного события сети к завершающему.

Произведем расчет графика, изображенного на рисунке 8.

Для всех работ, выходящих из исходного события сети, раннее начало всегда равно нулю, т.е.

T^рн_0-1 = 0; T^рн_0-2 = 0.

Для всех последующих работ, прежде чем определить величину раннего начала, необходимо раннее окончание работ, выходящих из исходного события сети. Эта величина для всех работ сетевого графика будет равна сумме раннего начала работы и ее продолжительности, т.е. в общем виде:

T^ро_i-j = T^рн_i-j + t_i-j . (1)

Для работ 0-1 и 0-2 ранние окончания будут равны 2 и 6 дней соответственно:

T^ро_0-1 = 0 + 2 = 2,

T^ро_0-2 = 0 + 6 = 6.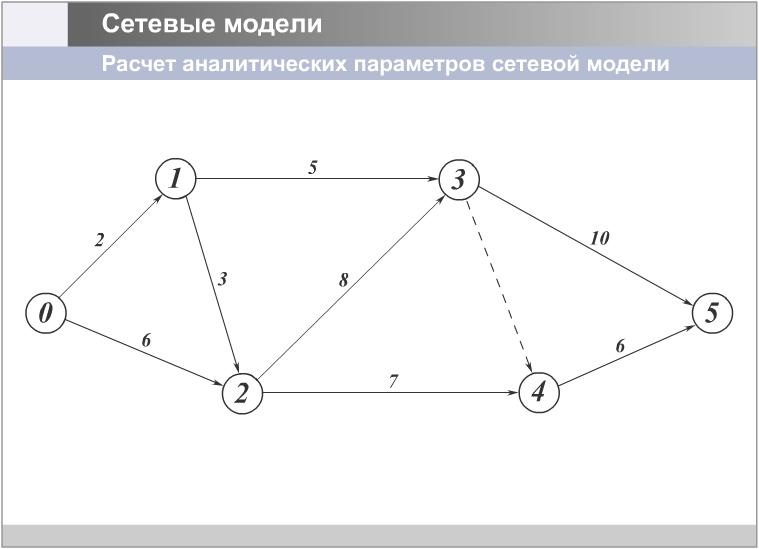


Рисунок 8. Пример сетевого графика
Если раннее окончание работы 0-1 равно 2, то могут ли работы 1-2 и 1-3 начинаться раньше, чем закончится работа 0-1? Очевидно, нет. Все работы, следующие за данной работой 0-1, могут начинаться только после самого раннего окончания работы 0-1, т.е. эта величина и есть раннее начало работ 1-2 и 1-3:

T^рн_1-2 = T^ро_0-1 ,

T^рн_1-3 = T^ро_0-1 .

Другими словами, раннее начало данной работы равно раннему окончанию предшествующей работы. Пользуясь этим правилом, определим раннее начало работы 1-2 и 1-3.

T^рн_1-2 = 2,

T^рн_1-3 = 2.

Какая выявляется закономерность? Работы, выходящие из исходного события, имеют одно и то же раннее начало, равное нулю. Работы, выходящие из события №1, тоже имеют одно и то же ранее начало – 2. Очевидно, все работы, которые выходят из одного и того же события, всегда имеют одну и ту же величину раннего начала.

Определив раннее начало для одной работы, мы можем записать его значение абсолютно для всех работ, выходящих из этого же события.

Используя формулу (1), определим раннее окончание работ 1-2 и 1-3.

Раннее окончание работы 1-2 будет равно раннему началу работы 1-2 (2 дня) плюс продолжительность этой работы (3 дня), т.е. 2+3 равно 5, и раннее окончание работы 1-3 будет равно раннее начало работы 1-3 (2 дня) плюс продолжительность этой работы (5 дней), т.е. 2+5 равно 7.

T^ро_1-2 = 2 + 3 = 5,

T^ро_1-3 = 2 + 5 = 7.

Далее определим раннее начало работы 2-3 и 2-4. Здесь важно напомнить, что сложное событие свершается только тогда, когда все работы, в том числе и самая большая по продолжительности, завершаются. Для работы 2-3 предшествующими работами являются 1-2 и 0-2, которые имеют ранние окончания соответственно 5 и 6. И раннее начало работы 2-3 будет определяться наибольшим ранним окончанием предшествующих работ. В виде формулы это можно записать так:

T^рн_i-j = мах T^ро_h-I , (2)

т.е. раннее начало данной работы равно максимальному раннему окончанию непосредственно предшествующих ей работ.

Используя формулы (1) и (2), определим раннее начало и окончание для всех остальных работ сетевого графика (рисунок).

T^рн_2-4 = 6 (точно так же, как и у работы 2-3);

T^ро_2-3= 6 + 8 = 14, T^ро_2-3 = 6 + 7 = 13;

T^рн_3-5 = мах [T^ро_2-3; T^ро_2-4] = 14.

Напомним, что логическая зависимость является полноправным элементом расчета параметров сети.

T^рн_3-4 = 14 (точно так же, как и у работы 3-5);

T^ро_3-5= 14 + 10 = 24, T^ро_3-4 = 14 + 0 = 14;

T^рн_4-5 = мах [T^ро_3-5; T^ро_3-4] = 14;

T^ро_4-5 = 14 + 6 = 20.

Поздние сроки начала и окончания каждой работы в отличие от ранних сроков определяются в обратном порядке – от завершающего события графика к исходному, т.е. справа налево по графику.

Вернемся к нашему сетевому графику. В предыдущем пункте было установлено, что самое раннее окончание работы 3-5 равно 24, а 4-5 равно 20. А чему равно самое позднее окончание этих работ? Очевидно, 24 дня, так как позже этого срока не должна заканчиваться ни одна работа.

Действительно, у работы 3-5 как раннее окончание, так и позднее окончание равны 24:

T^ро_3-5= 24,

T^по_3-5 = 24.

У работы 4-5 самое раннее окончание – 19, а самое позднее – 24.

T^ро_4-5= 24,

T^по_3-5 = 24.

А чему будут равны поздние начала этих работ? Очевидно, необходимо начинать эти работы в такой момент, чтобы успеть уложиться в заданную для данной работы продолжительность и закончить ее в самый поздний срок ее окончания. Например, работу 3-5 мы не можем начать на 15-й день, ибо мы не уложимся в самые поздние сроки ее окончания (15 + 10 = 25). Следовательно,

T^пн_3-5 = 24 – 10 = 14, а T^пн_4-5 = 24 – 6 = 18.

Таким образом, позднее начало данной работы равно позднему окончанию этой работы минус ее продолжительность:

T^пн_i-j = T^по_i-j - t_i-j . (3)

А чему будет равно позднее окончание работ 3-4 и 2-4? Эти работы мы должны закончить с таким расчетом, чтобы успеть начать в самое позднее время следующую работ 4-5, если же работы 3-4 или 2-4 закончим самое позднее через 19 дней, то самое позднее начало следующей работы будет также 19 дней, а мы определили, что T^пн_4-5 = 18. Таким образом, позднее окончание предшествующих работ должно всегда равняться самому позднему началу следующих. Отсюда

T^по_3-4= T^пн_4-5= 18,

T^по_2-4 = T^пн_4-5= 18.

Как видим, работы, входящие в пятое событие, имеют одну и ту же величину T^ро_i-5= 24 и работы, входящие в четвертое событие, имеют также одну и ту же величину T^по_i-4= 18. Следовательно, определив для одной из работ величину T^по_i-j, мы автоматически записываем эту же величину для всех других работ, входящих в это же событие.

Далее определим позднее начало работ 2-3 и 3-4 (3):

T^пн_2-4= 18 – 7 = 11,

T^пн_3-4= 18 – 0 = 18.

А чему будет равно время позднего окончания работ 2-3 и 1-3? Ведь из третьего события выходят две работы (3-5 и 3-1). Какое позднее начало принять в качестве позднего окончания работы 2-3 и 1-3? Работа 3-5 имеет T^пн_3-5 = 14, а работа 3-1 имеет T^пн_3-1 = 18. Совершенно очевидно, что в качестве T^по_i-j следует принимать минимальное T^пн_j-k (т.е. следующей работы). Если же мы поступим наоборот и возьмем в данном случае T^пн_3-4 = T^по_2-3 = 18, то получится, что работа 3-5 будет закончена: 18 + 10 = 28, а это нас не удовлетворяет, так как общая продолжительность работ по графику 24 дня.

Следовательно, позднее окончание данной работы всегда равно минимальному позднему началу непосредственно следующим за ней работам, т.е.

T^по_i-j = мin T^пн_j-k . (4)

Используя формулы (3) и (4), определим поздние сроки для всех остальных работ.

T^по_2-3 = 14,

T^по_1-3 = 14;

T^пн_2-3 = 14 – 8 = 6,

T^пн_1-3 = 14 – 5 = 9;

T^по_1-2 = 6,

T^по_0-2 = 6;

T^пн_1-2 = 6 – 3 = 3,

T^пн_0-2 = 6 – 6 = 0;

T^по_0-1 = 3,

T^пн_0-1 = 3 – 2 = 1.
Определение работ, составляющих критический путь, и резервов времени

Критические работы – это работы, которые не имеют никаких резервов времени и должны выполняться точно в заданную временную оценку по каждой работе.

Таким образом, для критических работ будут характерны следующие равенства:

T^рн_i-j = T^пн_i-j (5)

или

T^ро_i-j = T^по_i-j . (6)

В нашем сетевом графике эти равенства будут справедливы для работы:

0-2, у которой T^рн_0-2 = T^пн_0-2 = 0,

T^ро_0-2 = T^по_0-2 = 6;

2-3, у которой T^рн_2-3 = T^пн_2-3 = 6,

T^ро_2-3 = T^по_2-3 = 14;

3-5, у которой T^рн_3-5 = T^пн_3-5 = 14,

T^ро_3-5 = T^по_3-5 = 24.

Вводя определение понятия «путь», мы сравнивали продолжительность всех путей графика и выявляли путь, имеющий наибольшую продолжительность, т.е. критический путь. Все остальные пути были менее продолжительны, чем критический.

Если из продолжительности критического пути вычтем продолжительность любого другого, то мы получим полный резерв времени для всего пути.

Вернемся к ранее рассматриваемому сетевому графику.

Определим продолжительность пути, проходящего через события 0-1-3-5. Она будет равна 17. Резерв этого пути будет равен R_0-1-3-5 = 24 – 17 = 7. Что показывает полный резерв пути? Что можно увеличить продолжительность работ, лежащих на этом пути на 7 дней, не изменяя при этом конечного срока графика, не изменяя величины продолжительности критического пути.

Однако, оказывается, что без соответствующей проверки мы не имеем права этот резерв отнести на любую из работ, принадлежащих данному пути, потому что любая из работ может принадлежать одновременно нескольким путям, а не только одному данному пути. Например, работа 0-1. Она принадлежит пяти путям графика. Но если 7 дней мы на нее отнесем полностью, то, например, продолжительность пути 0-1-2-3-5 составит (((7 + 2 + 3 = 12) + 8) = 20) + 10 = 30, что не может нас устроить.

Значит, мы не имеем права на любую из работ отнести полный резерв пути без соответствующей проверки. Для того чтобы определить величину резерва для работы 0-1, необходимо рассмотреть все резервы пути, в которые входит эта работа, и взять наименьшую величину резерва. Но это весьма сложно, поэтому есть специальная формула, которая определяет полный резерв времени для каждой работы.

Полный резерв времени для данной работы (R_i-j) равен позднему ее окончанию минус раннее окончание данной работы либо позднему началу данной работы минус раннее начало этой работы.

R_i-j= T^по_i-j = T^ро_i-j , (7)

R_i-j= T^пн_i-j = T^рн_i-j . (8)

Полный резерв времени показывает, что данную работу можно начать позже на величину резерва либо увеличить продолжительность этой работы на величину резерва. При этом конечный срок графика не изменяется. Например, на работе 0-1 полный резерв времени показывает, что эту работу можно начинать не с нуля, а на один день позже или работать не два дня, как это указано в графике, а три дня.

Определить полные резервы времени для всех остальных работ:

R_0-2= 6 – 6 = 0,

R_1-2= 6 – 5 = 1,

R_1-3= 14 – 7 = 7,

R_2-3= 14 – 14 = 0,

R_2-4= 18 – 13 = 5,

R_3-5= 24 – 24 = 0,

R_3-4= 18 – 14 = 4,

R_4-5= 24 – 20.

Использование полного резерва времени на любой из работ говорит о том, что эта и все остальные работы этого пути (наименьшего) стали работами критическими. Если на работе 0-1 будет использован полный резерв, то изменится раннее начало следующих работ – 1-2 и 1-3, вместо 2 станет 3.

А сохранится ли полный резерв времени на следующий работе 1-2? Нет, так как T^рн_1-2 будет равно 3, следовательно, T^ро_1-2 = 3 + 3 = 6, т.е. работа будет критической. В этом и проявляется некоторое неудобство с использованием полного резерва времени. Получается так: кто стоит в графике дальше от исходного события, может не хватить резервов. Чтобы так не получилось, действует правило: разрешение на использование полного резерва работы может дать только руководитель проекта.

На работе 1-2, как и на работе 0-1 имеется один день полного резерва. Изменится ли раннее начало работ 2-3 и 2-4? Нет, не изменится. У этих работ раннее начало было 6. При использовании полного резерва оно стало 2+3+1 = 6. Оказывается, на работе 1-2, помимо полного, есть так называемый частный резерв.

Принципиальная разница между полным и частным резервом заключается в том, что использование частного резерва на работе не меняет ранних начал последующих работ.

Частный резерв равен раннему началу последующей работы минус раннее окончание данной работы:

r_i-j= T^рн_j-k – T^ро_i-j . (9)

Используя формулу (9), определим величины частного резерва для работы:

r_0-1= 2 – 2 = 0,

r_0-2= 6 – 6 = 0,

r_1-2= 6 – 5 = 1,

r_1-3= 14 – 7 = 7,

r_2-3= 14 – 14 = 0,

r_2-4= 14 – 13 = 1,

r_3-4= 14 – 14 = 0,

r_3-5= 24 – 24 = 0,

r_4-5= 24 – 20 = 4.

Частный резерв времени показывает, насколько можно увеличить продолжительность данной работы либо сдвинуть ее раннее начало, не изменяя при этом как раннего начала последующих работ, так и конечного срока графика.

Следует иметь в виду, что величина частного резерва никогда не превышает величину полного резерва времени, а сумма частных резервов всегда равна полному резерву пути.