ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ. Экзаменационный билет 1 Приближенные числа, их абсолютные и относительные погрешности. Значимые и верные числа
 Скачать 399.59 Kb. Скачать 399.59 Kb.
|
|
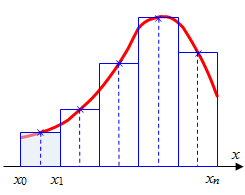
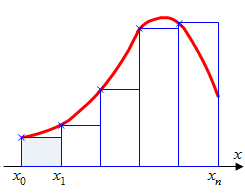
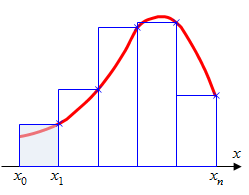
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1 1. Приближенные числа, их абсолютные и относительные погрешности. Значимые и верные числа. Приближенным числом а называется число, которое незначительно отличается от точного значения А. Под ошибкой или погрешностью А приближенного числа понимают разность между соответствующим точным числом и приближенным, т.е ∆a = A-a; Если А>а, то ошибка положительная, если меньше – отрицательная. Иногда знак ошибки неизвестен. В этом случае абсолютной погрешностью приближенного числа является выражение: ∆ = |∆a|; Абсолютной погрешностью А приближенного числа а называется абсолютная величина разности между соответствующим точным числом А и числом а т.е. : ∆ = |A-a|; Для точности данных измерений существенна абсолютная погрешность, приходящаяся на единицу длины, которая носит название относительной погрешности. Относительной погрешностью δ числа а называется отношение абсолютной погрешности дельта к приближенному значению этого числа: 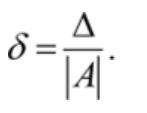 2. Постановка задачи численного интегрирования. Вычисление интеграла по формулам трапеций и парабол. Задача численного интегрирования состоит в замене исходной подынтегральной функции некоторой аппроксимирующей функцией (обычно полиномом). Если на частичном отрезке 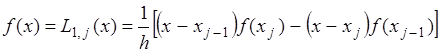 (2.9) (2.9)то искомый интеграл на частичном отрезке запишется следующим образом: 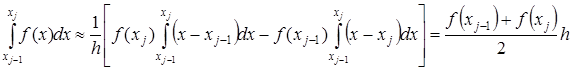 (2.10) (2.10)Тогда составная формула трапеций на всем отрезке интегрирования 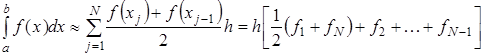 (2.11) (2.11)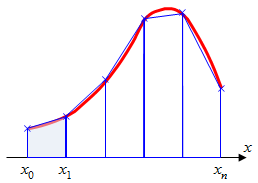 Рис.2.3. Интегрирование методом методом трапеций 2.2.3. Метод СимпсонаВ этом методе подынтегральная функция на частичном отрезке 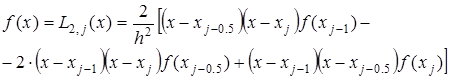 (2.12) (2.12)Проведя интегрирование, получим: 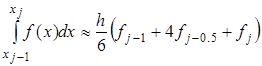 (2.13) (2.13)Это и есть формула Симпсона или формула парабол. Графическое представление метода Симпсона показано на рис.2.4. На каждом из сдвоенных частичных отрезков заменяем дугу данной кривой параболой. 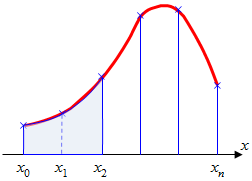 Рис.2.4.Метод Симпсона ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 2 Погрешности. Источники и классификация погрешностей. Различают абсолютную и относительную погрешность. Абсолютная - разность между истинным и вычисленным значением: Относительная – отношение абсолютной погрешности к приближенному (вычисленному) значению Источники погрешностей – причины их возникновения. Появляются вследствие: Неточного задания мат. Модели – численный метод или модель является лишь приближением к точному методу (например дифференцирование) или неучет некоторых особенностей метода. Погрешности появляющиеся в таких случаях называются методическими. Ошибки в исходных данных(любое измерение мб проведено с только какой то предельной точностью). В этом случае погрешность называется неустранимой, т.к. она не может быть уменьшена ни до начала решения задачи, ни в процессе решения. Вычислительных ошибок (ошибок окгругления). В результате этих ошибок появляются погрешности округления, связанные с ограниченностью хранимых разрядов. 2. Постановка задачи численного интегрирования. Вычисление интеграла по формулам трапеций и парабол. Задача численного интегрирования состоит в замене исходной подынтегральной функции некоторой аппроксимирующей функцией (обычно полиномом). Если на частичном отрезке 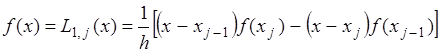 (2.9) (2.9)то искомый интеграл на частичном отрезке запишется следующим образом: 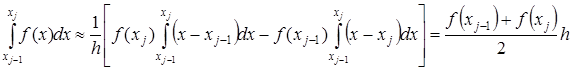 (2.10) (2.10)Тогда составная формула трапеций на всем отрезке интегрирования 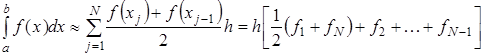 (2.11) (2.11) Рис.2.3. Интегрирование методом методом трапеций 2.2.3. Метод СимпсонаВ этом методе подынтегральная функция на частичном отрезке 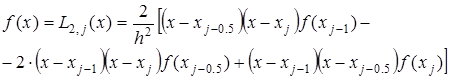 (2.12) (2.12)Проведя интегрирование, получим: 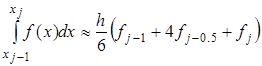 (2.13) (2.13)Это и есть формула Симпсона или формула парабол. Графическое представление метода Симпсона показано на рис.2.4. На каждом из сдвоенных частичных отрезков заменяем дугу данной кривой параболой.  Рис.2.4.Метод Симпсона ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 3 1. Этапы нахождения экстремумов функции. Метод золотого сечения. Для оптимизации (минимизации или максимизации) некоторой характеристики f(x) используют различные методы нахождения экстремумов этой самой функции. Метод золотого сечения. Пусть задана функция  Алгоритм  2. Постановка задачи численного интегрирования. Вычисление интеграла по формулам прямоугольников. Задача численного интегрирования состоит в замене исходной подынтегральной функции некоторой аппроксимирующей функцией (обычно полиномом). 2.2.1. Метод прямоугольниковОдним из простейших методов численного интегрирования является метод прямоугольников. На частичном отрезке 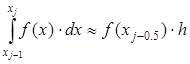 (2.6) (2.6)Подставив это выражение в (2.4), получим составную формулу средних прямоугольников: 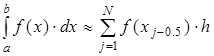 (2.7) (2.7)Графическая иллюстрация метода средних прямоугольников представлена на рис.2.2(a). Из рисунка видно, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из N прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы N элементарных прямоугольников. Формулу (2.7) можно представить в ином виде: 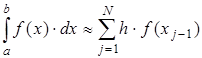 или или 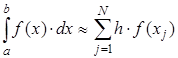 (2.8) (2.8)Эти формулы называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис.2.2(б, в). Однако из-за нарушения симметрии в формулах правых и левых прямоугольников, их погрешность значительно больше, чем в методе средних прямоугольников.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 4 1. Линейная аппроксимация. Метод наименьших квадратов. Аппроксимация – это определение параметров аналитической функции, описывающей набор точек, полученных в результате эксперимента Линейная аппроксимация предполагает расположение всех точек на одной прямой.  Решить эту систему можно методом наименьших квадратов, при котором среднеквадратичное отклонение экспериментальных данных от найденной аппроксимирующей функции наименьшее. Для вывода решения системы линейных уравнений методом наименьших квадратов перепишем выражение (4.5), с добавлением вектора погрешности Теперь задача сводится к минимизации квадрата нормы вектора погрешности Отсюда находим значение вектора X: Таким образом, метод наименьших квадратов сводится к нахождению обратной матрицы. 2. Постановка задачи численного интегрирования. Вычисление интеграла по формулам прямоугольников. Задача численного интегрирования состоит в замене исходной подынтегральной функции некоторой аппроксимирующей функцией (обычно полиномом). 2.2.1. Метод прямоугольниковОдним из простейших методов численного интегрирования является метод прямоугольников. На частичном отрезке 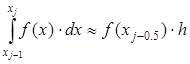 (2.6) (2.6)Подставив это выражение в (2.4), получим составную формулу средних прямоугольников: 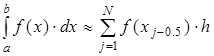 (2.7) (2.7)Графическая иллюстрация метода средних прямоугольников представлена на рис.2.2(a). Из рисунка видно, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из N прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы N элементарных прямоугольников. Формулу (2.7) можно представить в ином виде: 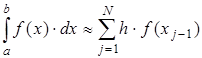 или или 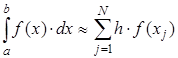 (2.8) (2.8)Эти формулы называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис.2.2(б, в). Однако из-за нарушения симметрии в формулах правых и левых прямоугольников, их погрешность значительно больше, чем в методе средних прямоугольников.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 5 1. Этапы нахождения корней нелинейного уравнения. Метод хорд. 2. Постановка задачи интерполирования функции. Линейная интерполяция. | ||||||||||||