3. элементарная теория погрешностей 1Понятие погрешности

• Название: 3. элементарная теория погрешностей 1Понятие погрешности
• Дата: 22.10.2020
• Размер: 237.5 Kb.
• Имя файла: 03-POGR.doc
• Тип: Документы; #144773

- -
Теория погрешностей

3.ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ

3.1Понятие погрешности

Приближенным числом а называется число, незначительно отличающееся от точного А и заменяющее последнее в вычислениях. Под ошибкой или погрешностью а приближенного числа а обычно понимается разность между соответствующим точным числом А и данным приближением, т.е.

а = А - а .

Абсолютной погрешностью  приближенного числа а называется абсолютная величина разности между соответствующим точным числом А и числом а, т.е.

 = А - а .

Если число А не известно, то по этой формуле нельзя определить абсолютную погрешность, Поэтому вместо неизвестной теоретической абсолютной погрешности вводят ее оценку сверху, называемую предельной абсолютной погрешностью .

Под предельной абсолютной погрешностью приближенного числа понимается всякое число, не меньшее абсолютной погрешности этого числа. Таким образом, если а - предельная абсолютная погрешность, то

 = А - а  а .

Отсюда следует, что точное число А заключено в границах:

а - а  А  а + а .

Для приближенного числа, полученного в результате округления, абсолютная погрешность а принимается равной половине единицы последнего разряда числа. Например, если значение а = 0.734 было получено округлением, то а = 0.0005 . При вычислениях на ЭВМ округления не производится, а цифры, выходящие за разрядную сетку машины, отбрасываются.

Абсолютная погрешность недостаточна для характеристики точности измерения или вычисления. Поэтому вводят понятие абсолютной погрешности, приходящуюся на единицу длины, которая называется относительной погрешностью.

Относительной погрешностью приближенного числа а называется отношение абсолютной погрешности этого числа к модулю соответствующего точного числа А (А0) т.е.

.

Так же как и для абсолютной погрешности вводят понятие предельной относительной погрешности. Под предельной относительной погрешностью _апонимают всякое число, не меньшее относительной погрешности этого числа. В качестве предельной относительной погрешности числа а можно принять число

.

Пример. Сравнить относительную погрешность двух приближенных чисел, полученных в результате округления: 98.1 и 0.000001 .

Решение. Абсолютные погрешности этих чисел равны половине единицы последнего разряда: ₁ = 0.05 и ₂ = 0.0000005 . Т.е. относительные погрешности равны:

₁ = 0.05 / 98.1 = 0.00051 = 0.051%

₂ = 0.0000005/0.000001 = 0.5 = 50% .

Таким образом первое число определено почти в тысячу раз точнее второго.

3.2Значащая цифра. Число верных знаков

Приведенные оценки погрешностей приближенных чисел верны, если в записи этих чисел все значащие цифры верны.

Известно, что всякое положительное число а может быть представлено в виде конечной или бесконечной дроби:

а = _m10^m + _m-110^m-1 + _m-210^m-2 + ... + _m-n+110^m-n+1 + ...

где _i - цифры числа а (_i = 0,1,2,...,9), причем старшая цифра _m  0, а m - некоторое целое число (старший десятичный разряд числа а ). Например,



В этом случае m = 3 и n = 6 .

Значащими цифрами считаются все цифры данного числа, начиная с первой ненулевой цифры. Например, в числе 0.067 - две значащие цифры, а в числе 24.40 - четыре. При изменении формы записи чисел количество значащих цифр не должно меняться. Поэтому, например, преобразования и равносильны, а записи и неравносильны.

Говорят, что n первых значащих цифр (десятичных знаков) приближенного числа являются верными, если абсолютная погрешность этого числа не превышает половины единицы разряда, выражаемого n-ой значащей цифрой, считая слева направо. Таким образом, если для приближенного числа а, заменяющего точное число А, известно, что

,

то по определению, первые n цифр _m, _m-1, ... , _m-n+1 этого числа являются верными.

Например, для точного числа А=35.97 число а=36.00 является приближением с тремя верными знаками, так как для m=1 и n=3, получим. .

В некоторых случаях удобно говорить, что число а является приближением точного числа А с n верными знаками в широком смысле, если абсолютная погрешность  = А - а не превышает единицы десятичного разряда, выражаемого n - ой значащей цифрой приближенного числа. Например, для точного числа А = 412.3567 число а = 412.356 является приближением с шестью верными знаками в широком смысле, так как .

Связь относительной погрешности приближенного числа с количеством верных знаков этого числа:

Если положительное приближенное число а имеет n верных десятичных знаков, то относительная погрешность не превосходит (1/10)^n-1 , деленную на первую значащую цифру данного числа, т.е.



где _m - первая значащая цифра числа а.

Если число а имеет больше двух верных знаков, т.е. n  2, то практически справедлива следующая формула:



Если приближенное число а имеет n верных десятичных знаков в широком смысле, то эти оценки следует увеличить в два раза.

Пример. Какова предельная относительная погрешность, если вместо числа взять число а = 3.14 ?

Решение. В этом случае _m = 3 и n = 3. Следовательно,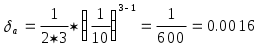



Для решения обратной задачи - определения количества n верных знаков числа, если известна его относительная погрешность, обычно пользуются приближенной формулой

 =  / a (a > 0) ,

где  - абсолютная погрешность числа а. Отсюда

.

Учитывая старший десятичный разряд числа , легко установить количество верных знаков числа а .

Пример. Приближенное число а = 24253 имеет относительную точность 1% . Сколько в нем верных знаков ?

Решение. Имеем .

Следовательно, число а имеет верными лишь две первые цифры (старший десятичный разряд равен двум); цифра сотен уже является сомнительной. Поэтому это число необходимо записывать в виде .

Этот же результат можно получить по приведенной выше формуле:

3.3Действия над приближенными числами

При сложении или вычитании чисел их абсолютные погрешности складываются. Относительная погрешность суммы заключена между наибольшим и наименьшим значениями относительных погрешностей слагаемых; на практике принимается наибольшее значение.

(a  b) = a + b .

При умножении или делении чисел друг на друга их относительные погрешности складываются.

;

При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени.



Погрешность суммы: на практике при сложении приближенных чисел поступают следующим образом:

- выделяют числа, десятичная запись которых обрывается ранее других и оставляют их без изменения;

- остальные числа округляют по образцу выделенных, сохраняя один или два запасных десятичных знака;

- производят сложение данных чисел, учитывая все сохраненные знаки;

- полученный результат округляют на один знак.

Пример. найти сумму приближенных чисел 0.348 0.1834 345.4 235.2 11.75 9.27 0.0849 0.0214 0.000354 .

Решение.

0.35 + 0.18 + 345.4 + 235.2 + 11.75 + 9.27 + 0.08 + 0.02 + 0.00 = 602.25 . После округления получаем 602.2 .

Полная погрешность результата складывается из трех слагаемых:

- суммы предельных погрешностей исходных данных:

₁=10^-3+10^-4+10^-1+10^-1+10^-2 +10^-2+10^-4+10^-4+10^-6 = 0.221301 < 0.222

.- абсолютной величины суммы ошибок (с учетом их знаков) округления слагаемых:

₂ =-0.002+0.0034+0.0049+0.0014+0.000354= 0.008054  0.009

- заключительной погрешности округления результатов:

₃ = 0.050 .

Следовательно,  = ₁ + ₂ + ₃  0.222+0.009+0.050 = 0.281 < 0.3 и, таким образом, искомая сумма равна 602.2  0.3 .
Погрешность разности: предельная абсолютная погрешность разности (u = x₁ - x₂) равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого:

_u = _x1 + _x2

Отсюда предельная относительная погрешность разности



где А - точное значение абсолютной величины разности чисел х₁и х₂ .

Если приближенные числа х₁ и х₂ достаточно близки друг к другу и имеют малые абсолютные погрешности, то число А - мало. В этом случае из этой же формулы следует, что предельная относительная погрешность может быть весьма большой, т.е. происходит потеря точности.

Пример. Найти разность двух чисел х₁ = 47.132 и х₂ = 47.111 .

Решение. Разность u = 47.132 - 47.111 = 0.021 . Предельная абсолютная погрешность разности равна _u = 0.0005+0.0005=0.001 .

Предельные абсолютные погрешности вычитаемого, уменьшаемого и разности равны:

_x1 = 0.0005/47.132 = 0.00001

_x2 = 0.0005/47.111 = 0.00001

_u = 0.001/0.021 = 0.05

Поэтому при приближенных вычислениях полезно преобразовывать выражения, вычисления числовых значений которых приводит к вычитанию близких чисел.
Погрешность произведения: относительная погрешность произведения нескольких приближенных чисел, отличных от нуля, не превышает суммы относительных погрешностей этих чисел:

  ₁ + ₂ + ... + _{n .}

Поэтому при вычислении произведения нескольких приближенных чисел применяют следующие правила:

- округляют эти числа так, чтобы каждое из них содержало на одну (или две) значащие цифры больше, чем число верных значащих цифр в наименее точном из сомножителей;

- в результате умножения сохраняют столько значащих цифр, сколько верных цифр имеется в наименее точном из сомножителей.

Пример. Найти произведение х₁ = 2.5 и х₂ = 72.397 .

Решение. После округления имеем х₁=2.5 и х₂=72.4 .Т.е. u=x₁x₂= 2.572.4 = 181 .
Погрешность частного: относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя.

Пример. Найти частное u = 25.7 / 3.6, если все написанные знаки делимого и делителя верны.

Решение. u = 25.7 / 3.6 = 7.14 . _u = _x1 + _x2 = 0.05/25.7 + 0.05/3.6 = 0.002 + 0.014 = 0.016 . Так как u = 7.14, то u = 0.016  7.14 = 0.11 . Поэтому u = 7.14  0.11 .
Пример. Найти относительную погрешность функции:



Решение. Используя формулы оценки погрешностей получаем



Из этой формулы следует, что при х  1 может получиться очень большая погрешность.

3.4Общая формула для погрешности

Основная задача теории погрешности заключается в следующем: известны погрешности некоторой системы величин, требуется определить погрешность данной функции от этих величин.

Пусть задана дифференцируемая функция u=(x₁,x₂, ... , x_n) и пусть x_i - абсолютные погрешности аргументов функции.
Тогда предельная абсолютная погрешность функции может быть вычислена по формуле:



Пример. Найти предельную абсолютную и относительную погрешности объема шара V =   d³ / 6 , если диаметр d = 3.7  0.05 см, а  = 3.14 .

Решение. Вычислим частные производные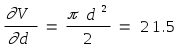

;

Тогда предельная абсолютная погрешность:

8.44*0.0016 + 21.5*0.05 = 0.013 + 1.075 = 1.088  1.1 см³ .

Поэтому

V =   d³ / 6 = 27.4  1.1 см³

_v = 1.088 / 27.4 см³ = 0.0397 см³  4 %
Предельная относительная погрешность функции вычисляется следующим образом: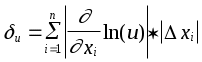



Пример. Для определения модуля Юнга по прогибу стержня прямоугольного сечения применяется формула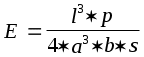



где l - длина стержня, aи b- измерения поперечного сечения стержня, s- стрела прогиба, p - нагрузка.

Вычислить предельную абсолютную погрешность при определении модуля Юнга, если p = 20 кг; _p = 0.1% ; a = 3 мм; _а = 1%; b = 44 мм; _b = 1%; l = 50 мм; _l = 1%; s = 2.5 см; _s = 1% .

Решение.

Ln(E) = 3  Ln(l) + Ln(p) - 3  Ln(a) - Ln(b) - Ln(s) - Ln(4) .

Отсюда, заменяя приращения дифференциалами, будем иметь



Следовательно:

_Е = 3  _l + _p + 3  _a + _b + _s = 3  0.01 + 0.001 + 3  0.01 + 0.01 + 0.01 = 0.081

Таким образом, предельная относительная погрешность составляет примерно 8% от измеряемой величины, т.е.

E = (2.10  0.17)  10 ⁶ кг.см² .

3.5Обратная задача теории погрешностей

На практике также важна обратная задача: каковы должны быть абсолютные погрешности аргументов функции, чтобы абсолютная погрешность функции не превышала заданной величины.

Эта задача математически не определена, так как заданную предельную погрешность u функции f(x₁,x₂,…,x_n) можно обеспечить, устанавливая по-разному предельные абсолютные погрешности x_i ее аргументов.

Простейшее решение обратной задачи дается так называемым принципом равных влияний. Согласно этому принципу предполагается, что все частные дифференциалы f/x_i  x_i одинаково влияют на образование общей абсолютной погрешности u функции f(x₁,x₂,…,x_n).

Тогда искомая формула легко получается из формулы предыдущего раздела:



Пример. Радиус основания цилиндра R = 2 м, высота цилиндра H = 3 м. С какими абсолютными погрешностями надо определить R и H, чтобы его объем V можно было вычислить с точностью до 0.1 м³ ?

Решение. Имеем и V = 0.1 м³.

Полагая R=2 м, H=3 м и =3.14 приближенно получаем

V/ = R²  H = 12

V/R = 2    R  H = 37.7

V/H =   R² = 12.6

Так как число параметров n = 3, то будем иметь

 = 0.1 / (3  12) < 0.003

R = 0.1 / (3  37.7) < 0.001

H = 0.1 / (3  12.6) < 0.003
Нередко при решении обратной задачи можно столкнуться с таким случаем, когда найденные по приведенной формуле предельные абсолютные погрешности отдельных независимых переменных окажутся настолько малыми, что добиться соответствующей точности при измерении этих величин практически невозможно. В таких случаях разумно уменьшают погрешности одной части переменных, чтобы добиться увеличения погрешностей другой части переменных.

Пример. С какой точностью надо измерить радиус круга R = 30.5 см и со сколькими знаками взять , чтобы площадь круга была известна с точностью до 0.1% ?

Решение. Имеем s =   R² . Используя общие правила работы с приближенными числами можно записать:


По принципу равных частей следует положить:

и

Отсюда  = 3.14*0.0005=0.00157  0.0016 и R  0.00025  R = 0.0076 см .

Таким образом если взять  = 3.14, то необходимо измерять R с точностью до тысячных долей сантиметра, что практически трудно осуществить.

Поэтому выгоднее поступить следующим образом: взять  = 3.142. В этом случае (по формуле в разделе о значащих цифрах) _ = 0.00016 . Тогда 2  R/R = 0.001 - 0.00016 = 0.00084 и R= 0.00084*30.5 / 2 = 0.01281 см, что уже можно выполнить практически.

3.6Основные источники погрешностей

Погрешности могут возникать на отдельных этапах решения задачи:

- Погрешность математической модели - в ней могут быть не учтены какие-либо важные черты рассматриваемой задачи.

- Погрешность исходных данных - это так называемые неустранимые погрешности. Поэтому следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности.

- Погрешность численного метода - это связано, например, с заменой интеграла суммой, усечением рядов при вычислении значений функции и т.д. Как правило, погрешность численного метода регулируема, т.е. она может быть уменьшена до любого разумного предела (например, изменением шага интегрирования и т.д.). Погрешность метода обычно стремятся довести до величины, в несколько раз меньшей погрешности исходных данных.

- Погрешности вычислений - при использовании ЭВМ неизбежны погрешности, связанные с ограниченностью разрядной сетки ЭВМ (обычно при этом просто отбрасываются лишние цифры). Еще одним источником погрешностей может быть перевод из одной системы счисления в другую. Это может привести к тому, что в новой системе счисления число становится иррациональным.
Уменьшение погрешностей:

1) Пусть требуется найти сумму пяти четырехразрядных чисел:

S = 0.2764 + 0.3944 + 1.475 + 26.46 + 1364 .

Складывая эти числа, а затем округляя полученный результат, получим S = 1393 .

При вычислении на ЭВМ округление происходит после каждого сложения, поэтому предполагая условно сетку машины четырехразрядной сложим эти числа в порядке их записи:

0.2764 + 0.3944 = 0.6708

0.6708 + 1.475 = 2.156

2.156 + 26.46 = 28.62

28.62 + 1364 = 1393 ,

т.е. получили правильный результат .

Если изменить порядок сложения, то получим следующий результат:

1364 + 26.46 = 1390

1390 + 1.475 = 1391

1391 + 0.3944 = 1391

1391 + 0.2764 = 1391

т.е. результат получился менее точным.

Поэтому сложение чисел необходимо проводить по мере их возрастания, т.е. в машинной арифметике из-за погрешности округления существенен порядок выполнения операций.

2) Подобные сложности могут возникать и в других ситуациях, например, при вычислении на ЭВМ значения (а + х)² величина х может оказаться такой, что результатом сложения а + х получится а (при х << a). В этом случае может помочь замена (а+х)² = а² + 2  а  х + х² .

3.7Устойчивость. Корректность. Сходимость

1. Устойчивость.Некоторые задачи весьма чувствительны к неточностям в представлении исходных данных. Эта чувствительность характеризуется так называемой устойчивостью.

Задача называется устойчивой по исходному параметру х, если решение y непрерывно от него зависит, т.е. малое приращение исходной величины x приводит к малому приращению искомой величины y .

Отсутствие устойчивости означает, что даже незначительные погрешности в исходных данных приводят к большим погрешностям в решении или даже вовсе к неверному результату. О таких задачах говорят, что они чувствительны к погрешностям исходных данных.

Примером такой задачи является отыскание действительных корней многочленов вида

(x - a)ⁿ = , 0 <  << 1 .

Изменение правой части на величину порядка приводит к погрешности корней порядка ^1/n .

2. Корректность. Задача называется поставленной корректно, если для любых значений исходных данных из некоторого класса ее решение существует, единственно и устойчиво по исходным данным.

Применять для решения некорректно поставленных задач численные методы, как правило, нецелесообразно, т.к. возникающие при этом погрешности округлений будут сильно возрастать в ходе вычислений, что приведет к значительному искажению результатов.

Для решения некоторых некорректных задач применяют так называемые методы регуляризации. Они основываются на замене исходной задачи корректно поставленной задачей. Последняя содержит некоторый параметр, при стремлении которого к нулю решение этой задачи переходит в решение исходной задачи.

3. Неустойчивость методов. Иногда при решении корректно поставленной задачи может оказаться неустойчивым метод ее решения, Например, для вычисления sin(x) можно использовать следующий степенной ряд: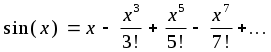



Если вычислить sin(x) при х = 0.5236 (30)при четырех верных знаках и не учитывать члены ряда, меньшие 10^-4, то можно получить

sin(0.5236) = 0.5236 - 0.02393 + 0.0003281 = 0.500 ,

т.е. получен правильный результат.

Если вычислить синус при х = 1470 = 4360+30, то можно получить sin(1470) = 0.5081 . Погрешность при этом составляет около 1%, что объясняется погрешностями округления и способом суммирования (слева направо, без учета величины членов).

Однако для данного ряда при х = 2190 (2190=6360+30) даже при учете членов ряда до 10^-8 и вычислениях с восемью значащими цифрами в результате аналогичных вычислений (суммирование слева направо) получается результат, не имеющий смысла sin(x)=-486.177 .

4. Сходимость. Сходимость означает близость получаемого численного решения задачи к истинному решению. Различают сходимость итерационного процесса и сходимость метода.

Сходимость итерационного процесса - этот процесс заключается в том, что для решения некоторой задачи и нахождения искомого значения определяемого параметра строится метод последовательных приближений. В результате многократного повторения этого процесса (или итераций) получают последовательность значений x₁, x₂, …, x_n, … Говорят, что эта последовательность сходится к точному решению x = a, если при неограниченном возрастании числа итераций предел этой последовательности существует и равен а . В этом случае имеют сходящийся вычислительный процесс.

Другой подход к понятию сходимости используется если задача с непрерывными параметрами заменяется задачей, в которой значения функции вычисляются в фиксированных точках (задачи дискретизации). Это относится, в частности, к численному интегрированию, решению дифференциальных уравнений и т.д. Здесь под сходимостью метода понимается стремление значений решения дискретной модели задачи к соответствующим значениям решения исходной задачи при стремлении к нулю параметра дискретизации (например, шага интегрирования).

3.8Задачи на вычисление погрешностей

1. Определить, какое равенство точнее:

9/11 = 0.818 4.24
Находят значения данных выражений с большим числом десятичных знаков:

a₁ = 9/11 = 0.81818… a₂ = 4.2426…

Вычисляют предельные абсолютные погрешности, округляя их с избытком:





Предельные абсолютные погрешности составляют: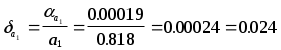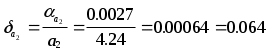

%

%

Так как , то 9/11=0.818 является более точным.

2. Определить сомнительные цифры числа, оставив верные знаки: а) в узком смысле; б) в широком смысле. Определить абсолютную погрешность результата:

а) 72.353 (0.026) б) 2.3544 =0.2%.
а) Пусть 72.353 (  0.026) = а. Согласно условию, погрешность _а = 0.026 < 0.05 . Это означает, что в числе 72.353 верными в узком смысле являются цифры 7, 2, 3. По правилам округления находят приближенное значение числа, сохранив десятые доли:

а₁ = 72.4;

Полученная погрешность больше 0.05; значит, нужно уменьшить число цифр в приближенном числе до двух:

а₂ = 72;

Так как < 0.5, то обе оставшиеся цифры верны в узком смысле.
б) Пусть а = 2.3544; _а = 0.2%; тогда _а = а * _а = 0.00471. В данном числе верными в широком смысле являются три цифры, поэтому округляем его, сохраняя эти три цифры:

а₁ = 2.35;

Значит, и в округленном числе 2.35 все три цифры верны в широком смысле.

3. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: а) в узком смысле; б) в широком смысле.

а) 0.4357 б) 12.384
а) Так как все четыре числа а = 0.4357 верны в узком смысле, то абсолютная погрешность _а = 0.00005, а относительная погрешность _а = 1 / (2 * 4 * 10³) = 0.000125 = 0.0125% .
б) Так как все пять цифр числа а = 12.384 верны в широком смысле, то _а = 0.001, а относительная погрешность _а = 1 / (1 * 10⁴) = 0.0001 = 0.01% .

4. Вычислить и определить погрешности результата:



где m = 28.3 ( 0.02), n = 7.45 ( 0.01), k = 0.678 ( 0.003)
Вычисляют

m² = 800.9; _m = 0.02 / 28.3 = 0.00071

n³ = 413.5; _n = 0.01 / 7.45 = 0.00135

_k = 0.003 / 0.678 = 0.00443

Тогда



_X = 2 _m + 3 _n + 0.5 _k = 0.00142 + 0.00405 + 0.00222 = 0.00769 = 0.77%

_X = 4.02 10⁵ * 0.0077 = 3.1 10³

Ответ: X = 4.02 10⁵ ( 3.1 10³) ; _X = 0.77%

5. Вычислить и определить погрешности результата:



где n = 3.0567 ( 0.0001) , m = 5.72 ( 0.02)
Имеем n - 1 = 2.0567 ( 0.0001) ; m + n = 5.72 ( 0.02) + 3.0567 ( 0.0001) = 8.7767 ( 0.0201) ; m - n = 5.72 ( 0.02) - 3.0567 ( 0.0001) = 2.6633 ( 0.0201) .

%

Ответ: N  2.54 ( 0.044): _N = 1.74% .

6. Вычислить, пользуясь правилами подсчета цифр

, где h = 11.8 и R = 23.67
V = 3.142 * 11.8² * (23.67 - 3.933) = 3.142 * 11.8² * 19.737 = 3.142 * 139.2 * 19.737 = 437.37 * 19.737 = 8630  8.63 10³ .