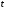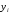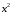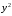1. Постановка задачи 3 Теоретические сведения 3
 Скачать 145.67 Kb. Скачать 145.67 Kb.
|
Оглавление1.Постановка задачи 3 2.Теоретические сведения 3 3.Преобразование исходных данных для построения модели Оукена 5 4.Построение модели Оукена 7 5.Анализ полученной модели 9 Заключение 13 Литература 14 1.Постановка задачиНа основании статистических данных об уровне безработицы и ВВП в РФ за 2001-2018 годы построить модель Оукена. Построение модели необходимо осуществить посредством решения системы нормальных уравнений и явный вид её решения при оценивании методом наименьших квадратов (МНК) линейной модели парной регрессии. Исходные данные:
Данные взяты с сайта https://gks.ru/bgd/regl/b20_11/Main.htm 2.Теоретические сведенияПредположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида: 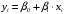 В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Метод наименьших квадратов позволяет получить такие оценки параметров β0и β1, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) y˜ минимальна: 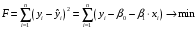 В процессе минимизации функции неизвестными являются только значения коэффициентов β0 и β1, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений: 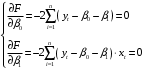 Если разделить обе части каждого уравнения системы на 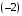 , раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида , раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида 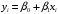 : :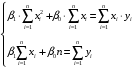 Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β0 и β1: 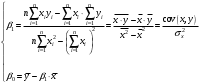 где 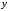 – среднее значение зависимой переменной; – среднее значение зависимой переменной; – среднее значение независимой переменной; – среднее значение независимой переменной;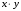 – среднее арифметическое значение произведения зависимой и независимой переменных; – среднее арифметическое значение произведения зависимой и независимой переменных;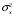 – дисперсия независимой переменной; – дисперсия независимой переменной;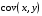 – ковариация между зависимой и независимой переменными. – ковариация между зависимой и независимой переменными.Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом: 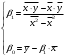 3.Преобразование исходных данных для построения модели ОукенаОсновные четыре этапа построения эконометрических моделей: построение спецификации эконометрической модели; сбор статистической информации об объекте-оригинале в виде конкретных значений экзогенных и эндогенных переменных, включённых в спецификацию модели; оценка неизвестных параметров модели (настройка модели); проверка адекватности оценённой модели (проверка соответствия настроенной модели объекту-оригиналу). Для построения эконометрической модели Оукена необходимо. 1) Построим спецификацию модели Оукена - эмпирической зависимости между темпом роста безработицы и снижением реального ВНП по сравнению с потенциально возможным. Будем считать, что темп прироста реального ВВП зависит от изменения уровня безработицы. Тогда модель можно представить в виде: 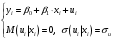 где 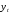 – темпы прироста реального ВВП, – темпы прироста реального ВВП, 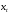 – изменения уровня безработицы, сигма – среднее квадратичное отклонение случайного остатка регрессии, равно константе; матожидание случайного остатка равно нулю. – изменения уровня безработицы, сигма – среднее квадратичное отклонение случайного остатка регрессии, равно константе; матожидание случайного остатка равно нулю.Преобразуем данные для построения модели. Рассчитаем значения 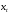 , как абсолютные приросты значений временного ряда , как абсолютные приросты значений временного ряда 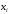 . Расчеты выполняем по формуле: . Расчеты выполняем по формуле: 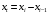
Рассчитаем значения 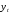 , как абсолютные приросты значений временного ряда , как абсолютные приросты значений временного ряда 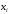 . Расчеты выполняем по формуле: . Расчеты выполняем по формуле: 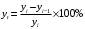
4.Построение модели ОукенаПреобразованный массив имеет 17 наблюдений и имеет вид:
Система нормальных уравнений. 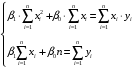 Для расчета параметров регрессии построим таблицу вспомогательных вычислений:
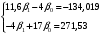 Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β0 и β1: 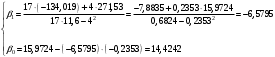 Таким образом, модель имеет вид: 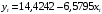 Параметры полученного уравнения можно интерпретировать следующим образом при увеличении прироста уровня безработицы на 1% темп прироста ВВП снижается на 6,5795% Проверим правильность построенной модели средствами MS Excel. Используем инструмент «Данные»  «Анализ данных» «Анализ данных»  «Регрессия». «Регрессия».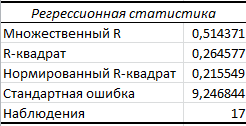 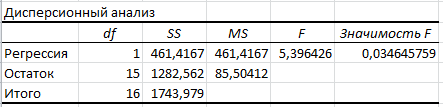  Из протокола регрессионного анализа видно, что уравнение регрессии имеет вид: 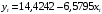 Следовательно, параметры модели найдены верно. 5.Анализ полученной моделиПостроение эконометрической модели подразумевает исследование ее качества. Проанализируем модель на основании данных, полученных при регрессионном анализе средствами MS Excel. Для определения взаимосвязи данных анализируем значения коэффициента корреляции и детерминации. Их значения получены из протокола регрессионного анализа. 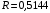 Связь результативного признака темпа прироста ВВП изменением уровня безработицы обратная и заметная Коэффициент детерминации равен: 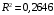 26,46% вариации темпа прироста ВВП объясняется вариацией изменения уровня безработицы, остальные 73,54% вариацией других признаков, не включенных в модель. Качество модели определяем с помощью средней ошибки аппроксимации: 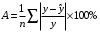 Строим таблицу промежуточных вычислений.
Отсюда: 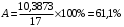 Так как значение средней ошибки аппроксимации больше 7%, точность модели нельзя назвать хорошей, поэтому данное уравнение нецелесообразно использовать для прогноза. Находим коэффициент эластичности по формуле: 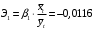 При увеличении изменения уровня безработицы на 1% темп прироста ВВП снижается на 0,0115% Значимость модели проверим с помощью критерия Фишера: 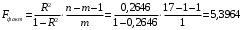 Фактические значения F– критерия сравниваем с табличным значением при 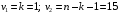 степенями свободы и уровне значимости степенями свободы и уровне значимости 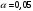 , , 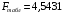 . . Так как 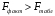 , то уравнение в целом признается значимым. , то уравнение в целом признается значимым.Значимость коэффициентов уравнения определяем с помощью t-статистик Стьюдента, значения которых берем из протокола регрессионного анализа. Сначала находим табличное значение t-статистики Стьюдента при уровне значимости ϒ=0,05 и степенях свободы 17–1–1=15, используя статистическую функцию СТЬЮДРАСПОБР(0,05;15). Получаем 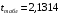 . .Сравниваем значения фактических t-статистик с табличным. 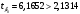 константа 0 значима; константа 0 значима;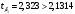 коэффициент 1 значим; коэффициент 1 значим;ЗаключениеВ результате расчетов посредством решения системы нормальных уравнений была получена модель Оукена зависимости темпа прироста ВВП от изменения уровня безработицы. 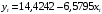 Возможна экономическая интерпретация параметров модели: При увеличении прироста уровня безработицы на 1% темп прироста ВВП снижается на 6,5795% Статистическая значимость уравнения проверена с помощью коэффициента детерминации и критерия Фишера. Установлено, что в исследуемой ситуации 26,46% общей вариабельности темпа прироста ВВП объясняется вариацией изменения уровня безработицы, остальные 73,54% вариацией других признаков, не включенных в модель. Установлено также, что параметры модели β0, β1 и константа статистически значимы. Средняя ошибка аппроксимации превышает 10%, следовательно качество модели нельзя назвать удовлетворительным. Для улучшения качество возможно применение ряда мер, выходящих за пределы данного исследования. ЛитератураКрасс, М. С. Математика в экономике. Базовый курс : учебник для бакалавров / М. С. Красс. — 2-е изд., испр. и доп. — М. : Издательство Юрайт, 2019. — 470 с. Красс, М. С. Математика в экономике: математические методы и модели : учебник для СПО / М. С. Красс, Б. П. Чупрынов ; под ред. М. С. Красса. — 2-е изд., испр. и доп. — М. : Издательство Юрайт, 2020. — 541 с. Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 3 : учебник и практикум для СПО / под ред. Н. Ш. Кремера. — 5-е изд., перераб. и доп. — М. : Издательство Юрайт, 2019. — 415 с. Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 3 : учебник и практикум для СПО / под ред. Н. Ш. Кремера. — 5-е изд., перераб. и доп. — М. : Издательство Юрайт, 2019. — 415 с. Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 1 : учебник и практикум для СПО / под ред. Н. Ш. Кремера. — 5-е изд., перераб. и доп. — М. : Издательство Юрайт, 2019. — 276 с. Малугин, В. А. Математический анализ для экономистов : учебник и практикум для СПО / В. А. Малугин. — 3-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 557 с. Рудык, Б. М. Математический анализ для экономистов : учебник и практикум для академического бакалавриата / Б. М. Рудык, О. В. Татарников. — М. : Издательство Юрайт, 2019. — 356 с. Смагин, Б. И. Экономико-математические методы : учебник для академического бакалавриата / Б. И. Смагин. — 2-е изд., испр. и доп. — М. : Издательство Юрайт, 2019. — 272 с. |