Ответы на вопросы Задание 2. 1 Поясните определение парной линейной регрессии. Поясните взаимосвязи экономических переменных
 Скачать 134.34 Kb. Скачать 134.34 Kb.
|
|
1/ Поясните определение парной линейной регрессии. Поясните взаимосвязи экономических переменных. 2\Дайте определение классической линейной регрессионной модели. 3\ В чем суть метода наименьших квадратов? 4\В чем заключается анализ точности определения оценок коэффициентов регрессии? 5\Для чего используется F-критерий Фишера? 6\ Что является мерой разброса зависимой переменной вокруг линии регрессии? 7\ Какие существуют критерии проверки гипотез, относящихся к коэффициентам регрессии? 8\Какова взаимозависимость различных критериев в парном регрессионном анализе? Ответы: 1.) Парная линейная регрессия — это модель, позволяющая моделировать взаимосвязь между значениями одной входной независимой и одной выходной зависимой переменными с помощью линейной модели, например, прямой. О парной линейной регрессии говорят, когда установлена зависимость между двумя переменными величинами (x и y). Парная линейная регрессия называется также однофакторной линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую переменную (зависимую переменную y). Например: рост цены ведет к снижению спроса, снижение процентной ставки ведет к увеличению инвестиций. Независимая переменная Х называется также входной, экзогенной , предикторной (предсказывающей), фактором, регрессом, факторной переменной. Зависимая переменная Y называется также выходной, результирующей, эндогенной, результативным признаком, функцией отклика. 2.) Если функция регрессии линейна (объясняющая переменная в уравнение регрессии входит в первой степени: M (Y x) = 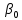 + +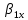 0), то регрессия называется линейной. 0), то регрессия называется линейной.Теоретическая модель классической парной линейной регрессии (зависимость между переменными в генеральной совокупности), или классическая линейная регрессионная модель (КЛРМ), имеет вид Y= 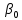 + +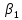 X+ɛ, X+ɛ,где Х рассматривается как неслучайная переменная, а Y и ɛ - как случайные величины; 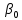 и и 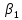 - теоретические коэффициенты (параметры) регрессии. - теоретические коэффициенты (параметры) регрессии.3.) Определение неизвестных параметров функции регрессии в эконометрике осуществляется на основе стандартного метода наименьших квадратов (МНК), метода наименьших квадратов. Принцип наименьших квадратов утверждает, что выбор параметров функции регрессии является оптимальным в случае, когда сумма квадратов отклонений эмпирических значений результирующей переменной от теоретических значений этой переменной, рассчитанной по функции регрессии, является минимальной. Математически принцип наименьших квадратов можно записать след. образом: Q (a,b)= 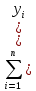 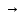 min minгде: 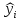 - расчетное значение тренда, - расчетное значение тренда, 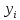 - фактическое значение тренда из ретроспективного ряда, n – число наблюдений - фактическое значение тренда из ретроспективного ряда, n – число наблюдений4.) Анализ точности определения оценок коэффициентов регрессии: Учитывая , что 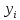 =M(y/х= =M(y/х=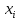 )+ )+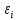 , получим , получим 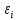 = =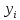 – M(y/х= – M(y/х=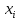 ), следовательно ), следовательноD( 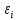 )=D( )=D(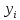 ). ).Предполагаем, что все измерения равноточные. Будем считать, что все дисперсии случайных отклонений равны между собой: D( 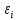 )= )=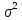 , i=1,n , i=1,nПолучим формулы связи дисперсий коэффициентов эмпирического уравнения регрессии D( 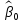 ), D( ), D(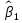 ) c дисперсией ) c дисперсией 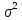 . Для этого представим формулы определения коэффициентов . Для этого представим формулы определения коэффициентов 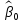 , ,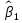 в виде линейных функций относительно значений переменной y: в виде линейных функций относительно значений переменной y: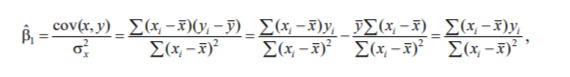 так как 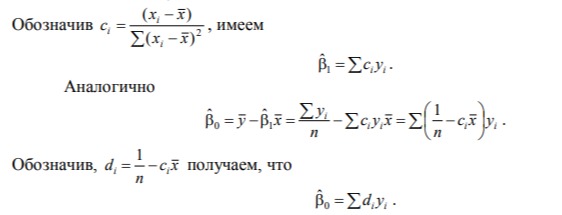 Так как предполагается, что дисперсия y постоянна и не зависит от значений x, то 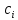 и и 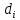 можно рассматривать как некоторые постоянные.Следовательно можно рассматривать как некоторые постоянные.Следовательно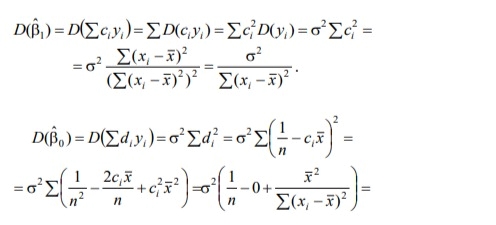 (1.1.) (1.1.)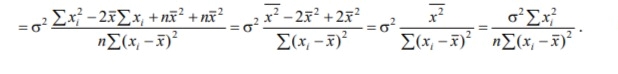 (1.2.) (1.2.)Из соотношений (1.1.), (1.2.) очевидны след.выводы: - Дисперсии оценок коэффициентов (D( 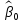 ), D( ), D(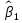 )) прямо пропорциональны дисперсии случайных отклонений - )) прямо пропорциональны дисперсии случайных отклонений - 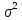 . Следовательно, чем больше фактор случайности, тем менее точным будут оценки. . Следовательно, чем больше фактор случайности, тем менее точным будут оценки.- Чем больше число наблюдений n, тем меньше дисперсии ошибок коэффициентов. Это вполне логично, чем большим числом наблюдений мы располагаем, тем вероятнее получение точных оценок. - Чем больше дисперсия объясняющей переменной x (разброс значений 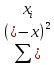 ),тем меньше дисперсия оценок коэффициентов. Другими словами, чем шире область изменения объясняющей переменной, тем точнее будут оценки. ),тем меньше дисперсия оценок коэффициентов. Другими словами, чем шире область изменения объясняющей переменной, тем точнее будут оценки.- Сростом числа наблюдений n до бесконечности дисперсии коэффициентов стремятся к нулю, что вместе с несмещенностью оценок 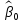 , , 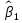 свидетельствует о состоятельности МНК – коэффициентов регрессии. свидетельствует о состоятельности МНК – коэффициентов регрессии.5.) F - критерий Фишера является параметрическим критерием и используется для сравнения дисперсий двух вариационных рядов. Критерий Фишера в основном применяется для сравнения малых выборок. Этому есть две весомые причины. Во-первых, вычисления критерия довольно громоздки и могут занимать много времени или требовать мощных вычислительных ресурсов. Во-вторых, критерий довольно точен (что нашло отражение даже в его названии), что позволяет его использовать в исследованиях с небольшим числом наблюдений. 6.) Мерой разброса зависимой переменной вокруг линии регрессии является несмещенная оценка дисперсии D( 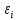 )= )=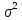 7.) Для проверки правдоподобия статистической гипотезы используют критерий значимости – метод проверки статистической гипотезы. Критерии проверки статистических гипотез (критерии значимости) можно разделить на три большие группы: Критерии согласия; Параметрические критерии; Непараметрические критерии. Критерии согласия называются критерии значимости, применяемые для проверки гипотезы о законе распределения генеральной совокупности, из которой взята выборка. Для проверки статистической гипотезы чаще всего используются следующие критерии согласия: критерий Шапиро-Уилки, критерий хи-квадрат, критерий Колмогорова-Смирнова. Параметрические критерии – критерии значимости, которые служат для проверки гипотез о параметрах распределений (чаще всего нормального). Такими критериями являются: t-критерий Стьюдента для независимых выборок, t-критерий Стьюдента для связанных выборок, F-критерий Фишера. Непараметрические критерии – критерии значимости, которые для проверки статистических гипотез не использует предположений о распределении генеральной совокупности. В качестве примера таких критериев можно назвать критерий Манна-Уитни и критерий Вилкоксона. 8.) В случае парного регрессионного анализа (и только парного регрессионного анализа) t-критерий для гипотезы 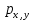 =0, F – критерий для коэффициента =0, F – критерий для коэффициента 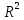 и t-критерий для гипотезы b=0 эквивалентны друг другу. и t-критерий для гипотезы b=0 эквивалентны друг другу. Поскольку 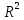 = =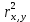 , F-статистика для коэффициента R2 является в точности квадратом t-статистики для Px,y. Как и следовало ожидать, критическое значение F будет равно квадрату критического значения t-статистики, при любом уровне значимости, и эти два теста всегда дают один и тот же результат, поскольку переменная, имеющая распределение Фишера, при условии, что первое число степеней свободы равно 1, имеет распределение квадрата Стьюдента. , F-статистика для коэффициента R2 является в точности квадратом t-статистики для Px,y. Как и следовало ожидать, критическое значение F будет равно квадрату критического значения t-статистики, при любом уровне значимости, и эти два теста всегда дают один и тот же результат, поскольку переменная, имеющая распределение Фишера, при условии, что первое число степеней свободы равно 1, имеет распределение квадрата Стьюдента.Более того, можно показать, что величина b будет значимо отличаться от нуля при использовании t-теста, если и только если F-тест значим. Используя тот факт, что Var( 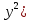 = =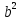 - Var(x), можем переписать выражение для стандартной ошибки величины b: - Var(x), можем переписать выражение для стандартной ошибки величины b: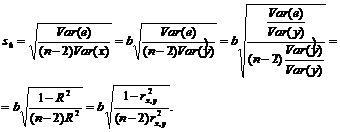 Следовательно, то есть t-статистика для проверки гипотезы b =0 такая же, как и t-статистика для проверки гипотезы 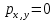 , а поскольку данные тесты используют одно и тоже распределение, то они будут давать одинаковый результат. , а поскольку данные тесты используют одно и тоже распределение, то они будут давать одинаковый результат.Таким образом, в случае парной регрессии проверка нулевой гипотезы H0:b=0 тестом Стьюдента и проверка нулевой гипотезы H0:R2=0 тестом Фишера дают одинаковые результаты. Эквивалентный результат дает тест Стьюдента для гипотезы |
