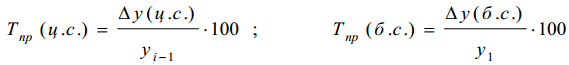Статистика. Статистика №1. Задача Данные об объеме розничного товарооборота на душу населения области

• Название: Задача Данные об объеме розничного товарооборота на душу населения области
• Анкор: Статистика
• Дата: 15.01.2022
• Размер: 91.04 Kb.
• Имя файла: Статистика №1.docx
• Тип: Задача; #331850

Задачи к теме 7
Задача 1. Данные об объеме розничного товарооборота на душу населения области:

Год	Продажа на душу населения, тыс. руб.
2005	30,9
2006	39,1
2007	52,7
2008	66,7
2009	79,8

Определите:

вид динамического ряда;

средний уровень динамического ряда;

абсолютные приросты, темпы роста и прироста цепные и базисные, абсолютное содержание 1% прироста;

средний абсолютный прирост, средний темп роста и прироста уровней динамического ряда.

Результаты расчетов представьте в таблице. Изобразите динамический ряд на графике. Сделайте выводы. Произведите аналитическое выравнивание динамического ряда, рассчитав уравнение тренда. Выполните экстраполяцию уровней динамического ряда по уравнению тренда на предстоящие два года.
Ответ

1. 
   Вид динамического - интервальный. Так как в данной таблице показан уровень размера розничного товарооборота за определенные года.
   

2. 
   Средний уровень динамического ряда считается по формуле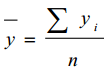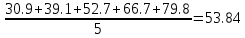
   

=

Среднегодовой розничный товарооборот на душу населения составляет 53,84

3. 
   Абсолютные приросты, темпы роста и прироста цепные и базисные, абсо-лютное содержание 1% прироста;
   

Расчет абсолютного прироста происходит по формуле

1. 
   39,1-30,9=8,2
   
2. 
   52,7-39,1=13,6
   
3. 
   66,7-52,7=14
   
4. 
   79,8-66,7=13,1
   

5. 
   39,1-30,9=8,2
   
6. 
   52,7-30,9=21,8
   
7. 
   66,7-30,9=35,8
   
8. 
   79,8-30,9=48,9
   

Темпы роста рассчитываются с помощью формулы

1) 39,1/30,9*100=126,5

2) 52,7/39,1*100=134,8

3) 66,7/52,7*100=126,6

4) 79,8/66,7*100=119,6
1) 39,1/30,9*100=126,5

2) 52,7/30,9*100=170,6

3) 66,7/30,9*100=215,9

4) 79,8/30,9*100=258,3

Темпы прироста рассчитываются с помощью формул

1. 
   8,2/30,9*100=26,5
   
2. 
   13,6/39,1*100=34,8
   
3. 
   14/52,7*100=26,6
   
4. 
   13,1/66,7*100=19,6
   

1. 
   8,2/30,9*100=26,5
   
2. 
   21,8/39,1*100=55,8
   
3. 
   35,8/52,7*100=67,9
   
4. 
   48,9/66,7*100=73,3
   

Абсолютное содержание 1% прироста


1)0,01*30,9=0,309

2)0,01*39,1=0,391

3)0,01*52,7=0,527

4)0,01*66,7=0,667

Годы	Объем розничного товарооборота	Абсолютный прирост		Темп роста, %			Темп прироста			Абсолютное содержание 1% прироста
		К предыдущему году	К базисному году	К предыдущему году	К базисному году	К предыдущему году		К базисному году
	1	2	3	4	5	6		7	8
2005	30,9	-	-	-	100	-		-	-
2006	39,1	8,2	8,2	126,5	126,5	26,5		26,5	0,309
2007	52,7	13,6	21,8	134,8	170,6	34,8		55,8	0,391
2008	66,7	14	35,8	126,6	215,9	26,6		67,9	0,527
2009	79,8	13,1	48,9	119,6	258,3	19,6		73,3	0,667

Расчет среднего абсолютного прироста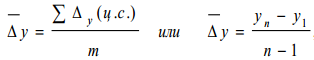




Средний темп прироста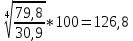




Средний уровень прироста


1) 126,5-100=26,5

2) 134,8-100=34,8

3) 126,6-100=26,6

4) 119,6-100=19,6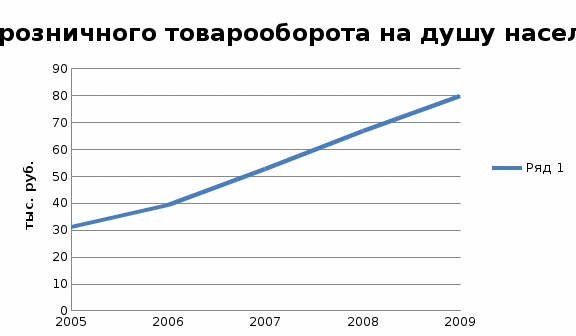



Задача 2. Данные о товарных запасах райпо на начало месяца:

Дата	1.01	1.04	1.07	1.10	1.01
Товарные запасы, тыс. руб.	1720	1631	1413	1856	1904

Определите вид динамического ряда и средний размер товарных запасов за год.

Ответ:
Динамический ряд: моментный, так как данные о товарных запасах представлены на определенный момент месяца.
Средний размер товарных запасов


Задача 3. Данные об объеме закупок сельскохозяйственных продуктов заготови-тельным предприятием за три года по кварталам, тыс. руб.:

Квартал	Первый год	Второй год	Третий год
I	1260	1345	1323
II	1315	1396	1495
III	1492	1687	1909
IV	1404	1519	1585
Итого	5471	5947	6312

Для анализа сезонности закупок исчислите индексы сезонности. Изобразите сезон-ную волну графически.
Ответ.

Для получения значений y найдем сумму уровней за три года по одноименным кварталам:

по 1 кварталу:1260+1345+1323=3928
по 2 кварталу:1315+1396+1495=4206
по 3 кварталу:1492+1687+1909=5088
по 4 кварталу:1404+1519+1585=4508

Итого: 5471+5947+6312=17730
Вычислим среднеквартальный уровень:

За 1 квартал: 3928/3=1309,3

За 2 квартал:4206/3=1402

За 3 квартал:5088/3=1696

За 4 квартал:4508/3=1502,7

Итого: 17730/3=1477,5
Вычислим индекс сезонности:

1 квартал:1309,3/1477,5*100=88,6

2 квартал: 1402/1477,5*100=94,9

3 квартал: 1696/1477,5*100=114,8

4 квартал: 1502,7/1477,5*100=101,7

Итого: 1477,5/1477,5*100=100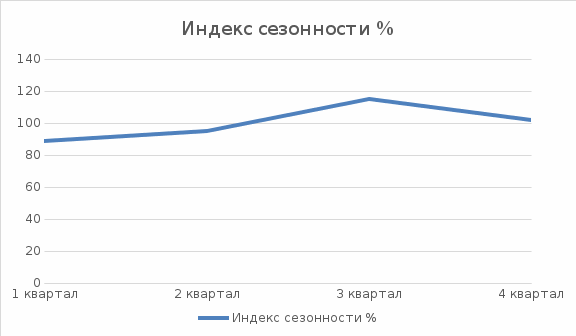