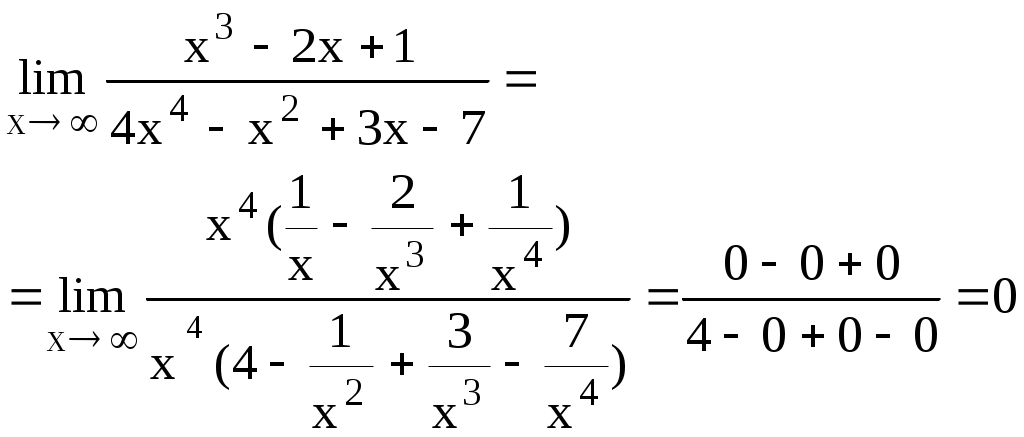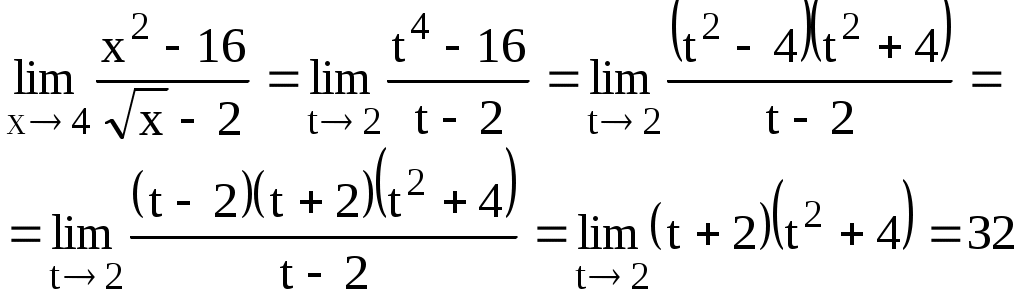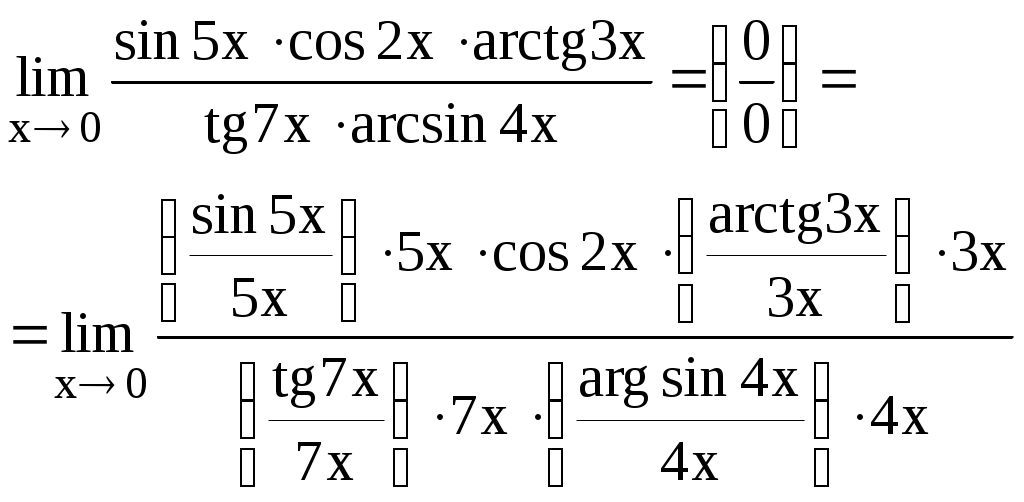1. Предел числовой последовательности и функции

• Название: 1. Предел числовой последовательности и функции
• Дата: 14.10.2021
• Размер: 296 Kb.
• Имя файла: Predel.doc
• Тип: Документы; #247338

1. Предел числовой последовательности и функции
Определение 1. Число А называется пределом функции f(x) в точке a, если для любого 0 найдётся такое число 0, что из неравенства следует неравенство .

Определение 2. Число А называется правым (левым) пределом функции f(х) в точке а, если для любого найдётся такое число , что из неравенства следует неравенство .

Для обозначения правого (левого) предела функции f(x) в точке а используют следующую символику: .

Критерий существования предела. Для того, чтобы в точке существовал предел функции f(x), необходимо и достаточно, чтобы существовали и были равны между собой оба односторонних предела

.

Достаточно распространенными в курсе математики являются последовательности, то есть функции , заданные на множестве натуральных чисел N. Чтобы подчеркнуть, что аргумент такой функции принимает только значения из множества натуральных чисел, его обозначают не х, а n. Для последовательностей f(n) достаточно часто возникает необходимость найти ее предел при неограниченном возрастании аргумента n (при ).

Определение 3. Число В называется пределом последовательности f(n), если для произвольного существует такое число , что для всех выполняется неравенство .

При вычислении пределов обычно используют не определение предела, а теоремы о пределах и приёмы, которые мы обобщим, оформив результат в форме табл. 1.

Таблица 1

Практическое вычисление пределов

Вычисление предела функции
Основные этапы	Пример
1.Пользуясь непрерывностью функции f(x), пробуем подставить значение x = а в функцию f(x)
2.Если вычисляется предел при х и имеется неопределенность типа , то пробуем в числителе и знаменателе вынести за скобки переменную в наивысшей степени (или числитель и знаменатель делим на переменную в наивысшей степени)
3.Если в результате подстановки х=а получили выражение типа , то:
а) пробуем числитель и знаменатель разложить на множители	=

Продолжение табл.1

1	2
б) если в числитель или знаменатель входят выражения с квадратным или кубическим корнями, то умножаем числитель и знаменатель на соответствующие выражения, чтобы избавиться от заданных корней (иногда вводят новую переменную)	1 способ 2 способ Обозначим . Тогда . При x, t. Тогда
в) если под знаком предела стоят тригонометрические или обратные тригонометрические функции, то такие пределы приводятся к 1-му замечательному пределу	Сократив числитель и знаменатель на переменные, которые стоят за скобками, учитывая, что , и учитывая первый замечательный предел и его вариации, получаем, что искомый предел равен:

При нахождении пределов вида следует иметь в виду, что:

1. 
   если существуют конечные пределы и , то
   
2. 
   если и , то вопрос о нахождении предела С решается непосредственно;
   
3. 
   если , то есть имеем неопределённость вида , то используем 2-ой замечательный предел или
   

Пример 1. Найти

Решение. Здесь ,

следовательно, .

Пример 2. Найти .

Решение. Имеем

Поэтому .

Пример 3. Найти .

Решение. Здесь 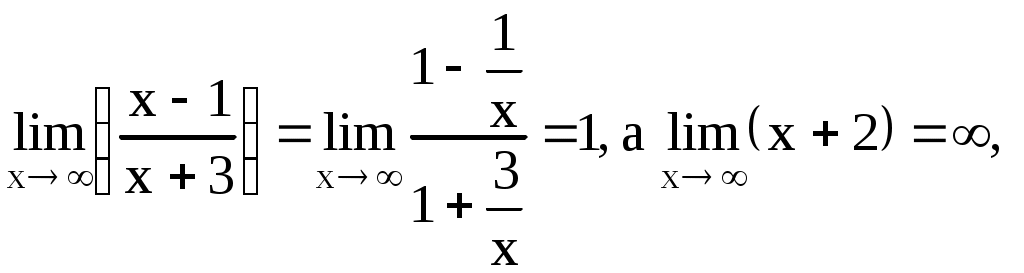то есть имеем неопределённость вида . В этом случае, прежде чем применить 2-ой замечательный предел, произведём следующие преобразования:



Можно найти предел проще, не прибегая к общему приёму, а именно
Замечание. Если существует и положителен то

2. 
   Cравнение бесконечно малых функций
   

Определение. Если , то f(x) называется бесконечно малой при xa.

Пусть функции х и х являются бесконечно малыми при хх . Тогда:

1. 
   если , то (х) называется бесконечно малой функцией более высокого порядка, чем (х) при хх ;
   
2. 
   если , где А -конечное число, отличное от нуля, то (х) и (х) называются бесконечно малыми функциями одного порядка при хх ;
   
3. 
   если , то (х) и (х) называются эквивалентными бесконечно малыми функциями при хх . При этом пишут:
   

х(х).

Аналогичные определения можно сформулировать и при х х х хх 0, хх +0.

При вычислении пределов пользуются следующей теоремой: предел произведения или частного бесконечно малых функций не изменится, если любую из них заменить эквивалентной ей бесконечно малой функцией.

Пусть х  бесконечно малая функция при хх . Имеют место следующие эквивалентности при х0:

1) sinхх 2) tgхх

3) arcsinxx 4) arctgx(x

5) log(1+x ; 6) ln(1+xx

7) a xlna; 8) e x

9. 
   (1+x а(х).
   

Пример 1. Найти .

Решение. Так как sin x  x, a arctg 2x  2x при х0, то

.
Пример 2. Найти .

Решение. Здесь при х, поэтому

.

3. Непрерывность функции

Функция f(x) называется непрерывной в точке а, если:

1) эта функция определена в некоторой окрестности точки а;

2) существует предел ;

3) этот предел равен значению функции в точке а, т.е.

Если функция непрерывна в каждой точке некоторой области, то она называется непрерывной в этой области.

Те точки области определения функции, в которых функция не является непрерывной, называются точками разрыва функции.

Различают разрывы двух видов.

1. 
   Если в точке а существуют односторонние пределы функции, но, по крайней мере, один из них не равен значению данной функции в точке а, то говорят, что функция f(x) в точке а имеет разрыв первого рода. При этом возможны следующие случаи:
   

f(a0)=f(a+0)f(a)

(в этом случае говорят, что функция f(x) в точке а имеет устранимый разрыв);

f(a0)f(a+0)

(в этом случае говорят, что функция f(x) в точке а имеет разрыв с конечным скачком. При этом число f(a+0)  f(a0)называют скачком функции f(x) точке а).

2. 
   Функция f(x) в точке а имеет разрыв второго рода, если в этой точке по крайней мере, один из односторонних пределов бесконечен или вовсе не существует.
   

Функция f(x) называется непрерывной на отрезке , если она непрерывна в каждой точке этого отрезка, причём в точке а она непрерывна справа (f(a+0)=f(a)), а в точке в - слева (f(b0)=f(b)).

Непрерывные на отрезке функции обладают рядом важных свойств. Приведём одно из них.

Пусть функция f(х) непрерывна на отрезке и на концах этого отрезка принимает значения разных знаков. Тогда на интервале существует такая точка c, в которой данная функция равна нулю.

В задачах 1-5 определить, какого рода разрывы имеют следующие функции в точке а

Пример 1.

Решение. Если х30, то и . Если х3+0, то и . Так как один из односторонних пределов бесконечен, следовательно, а=3-точка разрыва 2-го рода.

Пример 2. , а=1.

Решение. Выделим целую часть . Если , то и . Если х1+0, то и .

Таким образом, функция при х1 не имеет ни левого, ни правого конечного предела. Следовательно, х=1 является точкой разрыва 2-го рода.

Пример 3. , а = 5.

Решение. Если , то и . Если , то и . Итак, при х 5 фу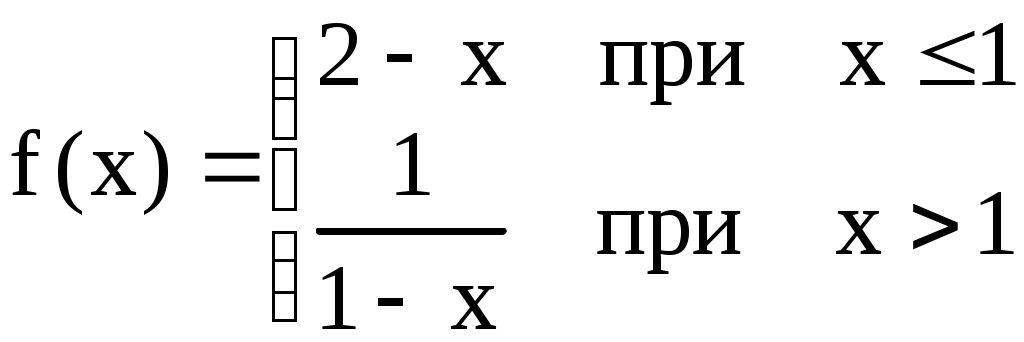нкция имеет левый и правый конечные пределы, причём эти пределы различны. Следовательно, х = 5 является точкой разрыва 1-го рода. Разность между правым и левым пределами (скачок) в точке разрыва равна .

Пример 4. , а = 1.

Решение. ,

. Итак,

, но не равны , значит, а=1 является устранимой точкой разрыва.
Пример 5. ,

Решение. Если х10, то . Если х1+0, то . Один из односторонних пределов бесконечен, следовательно, -точка разрыва 2-го рода.

4. Дифференцирование функции

Пусть функция определена в некоторой окрестности точки .

Определение. Предел отношения приращения функции в этой точке (если он существует) к приращению аргумента, когда , называется производной функции f(x) в точке .

Обозначения: 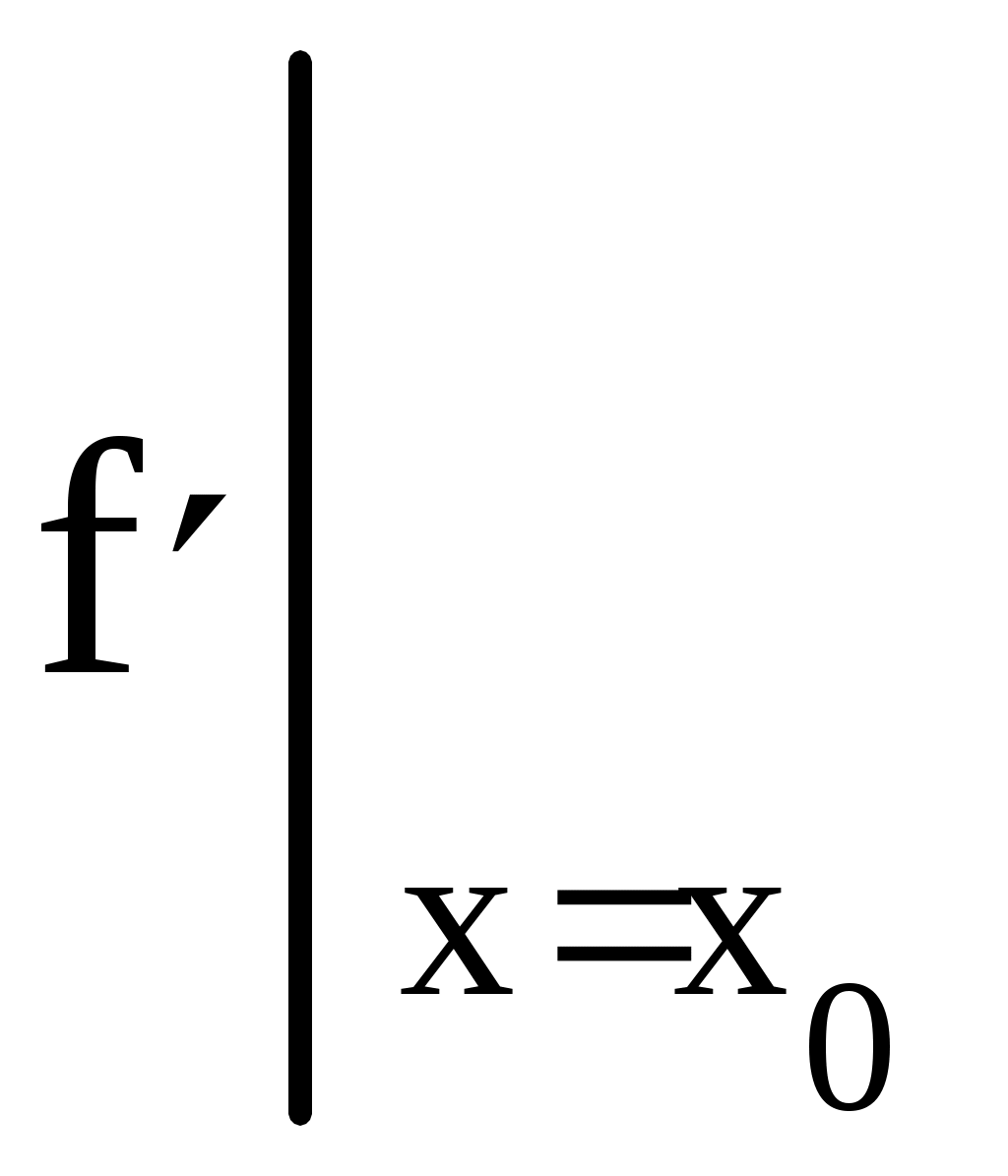или или или . Таким образом,

.

Вычисление производной называется дифференцированием функции.

Так как дифференцирование функций с использованием только таблицы производных элементарных функций и основных правил дифференцирования не вызывает особых затруднений, то мы остановимся лишь на приемах вычисления производных сложных функций.