ответ на билеты по экзамену 12.11.2013. 1. Предмет геодезии
 Скачать 2.04 Mb. Скачать 2.04 Mb.
|
|
12. Измерение горизонтальных углов полным приемом теодолитом, точность. Под горизонтальным углом понимают линейный угол двугранного угла, образованного плоскостями Р и N (рис.1). 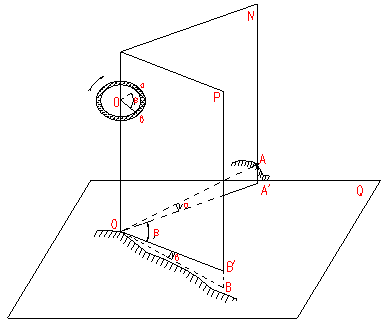 Рис. 1 Горизонтальный и вертикальные углы Горизонтальный угол определяется углом β между проекциями сторон ОА и ОВ на горизонтальную плоскость Q, т.е. углом АОВ –измеряется от 0° до 360° (вкл). Если деление на круге подписаны по ходу часовой стрелки, а отчеты по градуированной окружности обозначить через а и в, то: β = в – а. Описанный принцип измерения углов на местности реализуется в угломерном приборе – теодолитом с помощью которого измеряют горизонтальные и вертикальные углы. По точности теодолиты подразделяются на: - высокоточные (Т1 его точность равна t=1”); - точные (Т2, Т5 – их точность следующая: t = 2” и t =5” соответственно); - технические (2Т30 – его точность равна t= 30”). Измерение угла способом приёмов Обычно при съемке измеряют углы вправо по ходу лежащие. Ход от А → С → В. А – называется задней точкой, В – называется передней точкой. Движением алидады (при неподвижном лимбе) наводят сначала точку перекрестия нитей трубы на заднюю веху (предмет) А и делают отсчет по лимбу при помощи отсчетных устройств. Полученный результат называют отсчетом назад и обозначают а (рисунок 2). 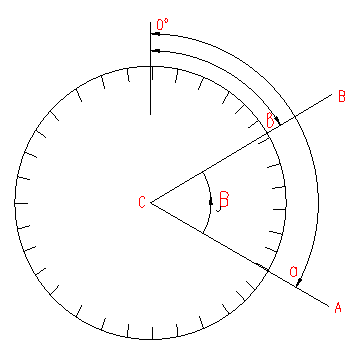 Рис. 2 Измерение горизонтального угла Затем, вращая алидаду, визируют на переднюю веху (предмет) В и получают отсчет вперед в: β = а – в. 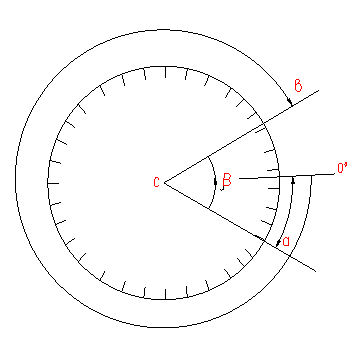 Рис. 3 Измерение горизонтального угла Если нуль лимба расположится между сторонами АС и СВ, то отсчет назад будет меньше отсчета вперед. В этом случае необходимо к отсчету назад прибавить 3600. Β = а – в + 3600. Затем трубу переводят через зенит. Измерение повторяют. Если теодолит повторительный, то рекомендуется перед вторым измерением лимб повернуть так, чтобы новое измерение было сделано на другой части лимба. Каждое такое измерение называется полуприемом. Два таких измерения составляют полный прием. Расхождение результатов измерения между первым и вторым полуприемами не должно превышать двойной точности теодолита. Если δ < 2 t, результат усредняют. 13. Сущность и назначение теодолитной съемки. Ситуационную съемку выполняют с помощью теодолита, поэтому ее называют теодолитной. В результате теодолитной съемки получают на плане положения контуров и предметов местности без рельефа. При теодолитной съемке сначала производят полевые измерения, а затем на основе полученных результатов измерений составляют планы местности. Теодолитную съемку применяют для съемки равнинной местности со сложной ситуацией (населенные пункты, застроенные участки, железнодорожные станции и др.). 14. Этапы полевых работ при теодолитной съемке. Теодолитную съемку применяют для съемки равнинной местности со сложной ситуацией (населенные пункты, застроенные участки, железнодорожные станции и др.). Этапы полевых работ при теодолитной съемке: 1) производится рекогносцировка (осмотр) местности устанавливается граница съемочного участка, 2) создание съемочного геодезического обоснования проложением теодолитных ходов и привязка их к существующим опорным геодезическим пунктам; 3) съемка ситуации (контуров) местности. 15. Способы съемки ситуации при теодолитной съемке, абрис. 1) Способ полярных координат (рис.1). Для определения планового положения снимаемых точек ситуации измеряют горизонтальные углы одним полуприемом и соответствующие длины до точек при помощи ленты, рулетки или дальномера. В этом случае сторона теодолитного хода принимается за полярную ось, а опорная точка за полюс 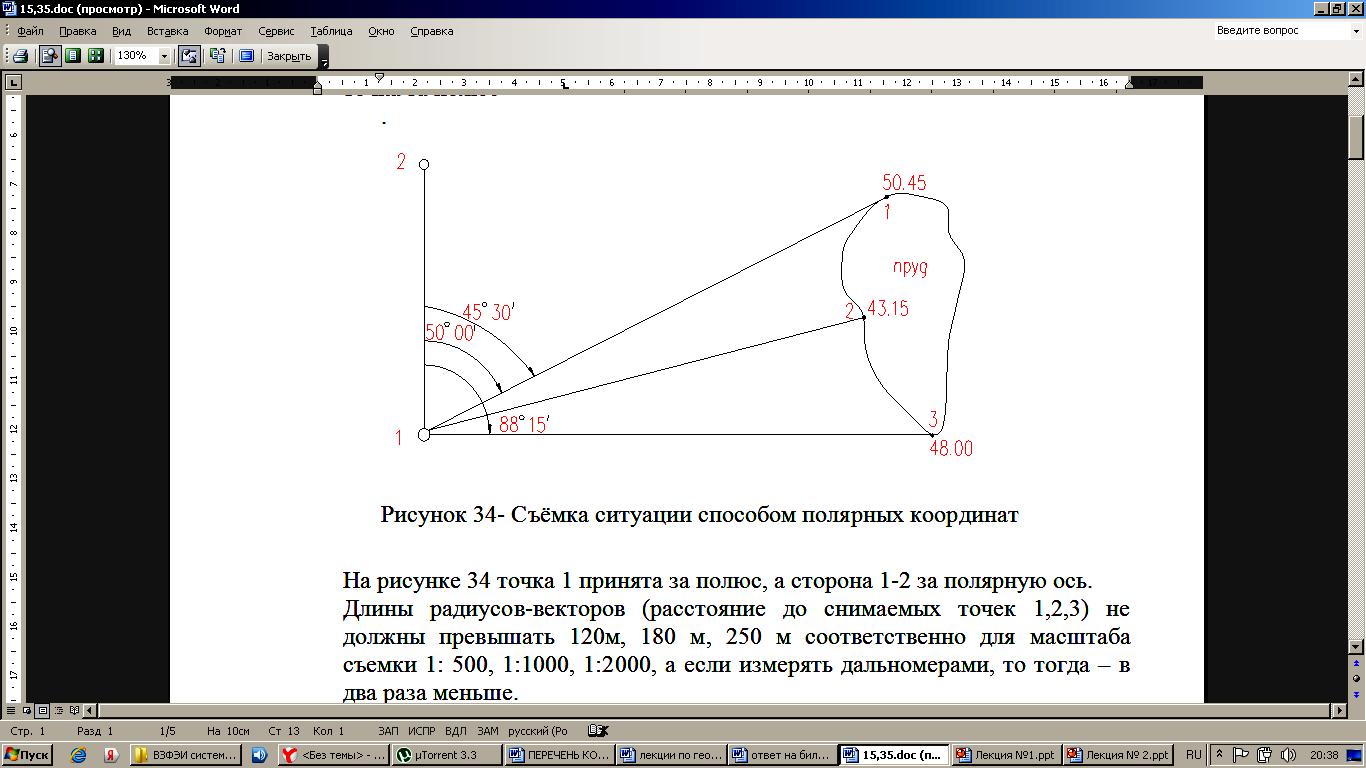 Рис.1 Съёмка ситуации способом полярных координат На рисунке 1 точка 1 принята за полюс, а сторона 1-2 за полярную ось. Длины радиусов-векторов (расстояние до снимаемых точек 1,2,3) не должны превышать 120м, 180 м, 250 м соответственно для масштаба съемки 1: 500, 1:1000, 1:2000, а если измерять дальномерами, то тогда – в два раза меньше. Суть способа заключается в том, что точки определяются в системе полярных координат, т.е. горизонтальными углами, образованными начальным направлением и расстоянием от точки полюса до снимаемых точек, расстояния определяются нитяным дальномером. 2) Способ прямоугольных координат (рис.2). Этот способ применяется при съемке вытянутых в длину объектов и близко расположенных к сторонам теодолитного хода (рисунок 2). Для съемки сторону теодолитного хода принимают за ось абсцисс, а начальная точка линии – за начало абсцисс (х). Например, со стороны теодолитного хода т.т. 5-6 необходимо снять проселочную дорогу. 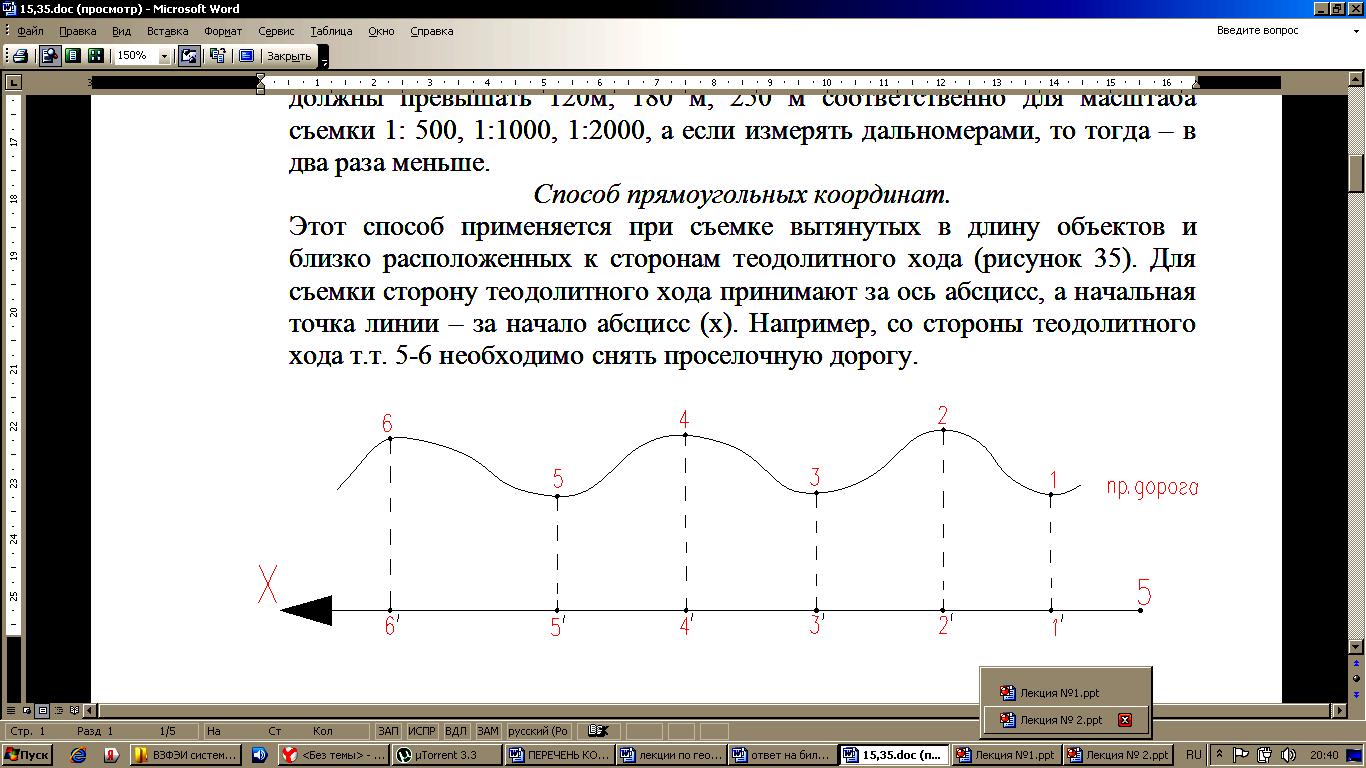 Рис.2 Способ прямоугольных координат Из точек 1-6 снимаемой дороги опускают перпендикуляры на линию 5-6. Проекции измеряемых лентой отрезков 51’,52’,53’,54’,55’,56’ являются абсциссами, а проекции перпендикуляров 11’,22’,33’,44’,55’,66’ являются ординатами точек 1-6 дороги. Измеренные значения абсцисс и ординат заносят в абрис. При съемке этим способом длины перпендикуляров (y) не должны превышать 4, 6, 8 м соответственно для масштабов съемки 1:500, 1:1000, 1:2000. Применяется при съемке ситуации и местных предметов, имеющих правильные геометрические формы, например, зданий, а также криволинейных контуров, например, рек, дорог и т.д. Перпендикуляры опускаются из снимаемых точек контура местности на стороны теодолитного хода. 3) Способ угловых засечек (рис.3). Этот способ применяется при съемке труднодоступных отдаленных точек. Плановое положение снимаемых точек определяется измерением двух прилежащих углов β2 и β3 составленных стороной теодолитного хода и направлением на снимаемую точку. На рисунке 3 снимаемой точкой является точка А на противоположном берегу реки относительно стороны 2-3. 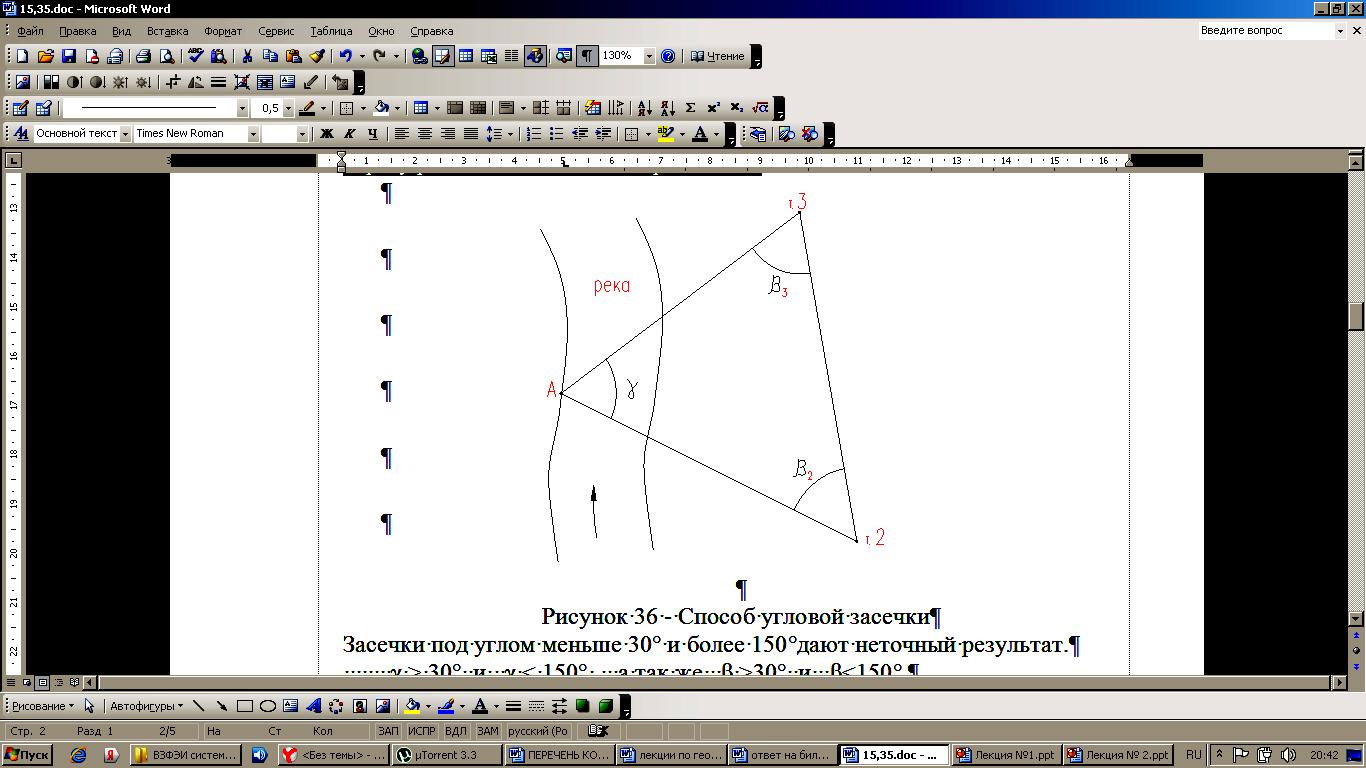 Рис.3 Способ угловой засечки Засечки под углом меньше 30° и более 150°дают неточный результат. γ > 30° и γ < 150° , а так же β >30° и β<150°. Этот способ выгодно применять при съемке труднодоступных контуров, например при съемке противоположного берега реки. В этом случае одним полуприемом измеряют нужные углы. При построении на плане пересечение прямых под этими углами дает необходимые точки 4) Способ линейных засечек (рис.4). Этот способ применяется при съемке близко расположенных объектов к опорным точкам (рисунок 37). Для съемки измеряют длины трех сторон треугольника. Так, например, для съемки положения колодца принят этот способ от точек 7 и створной точки 1. 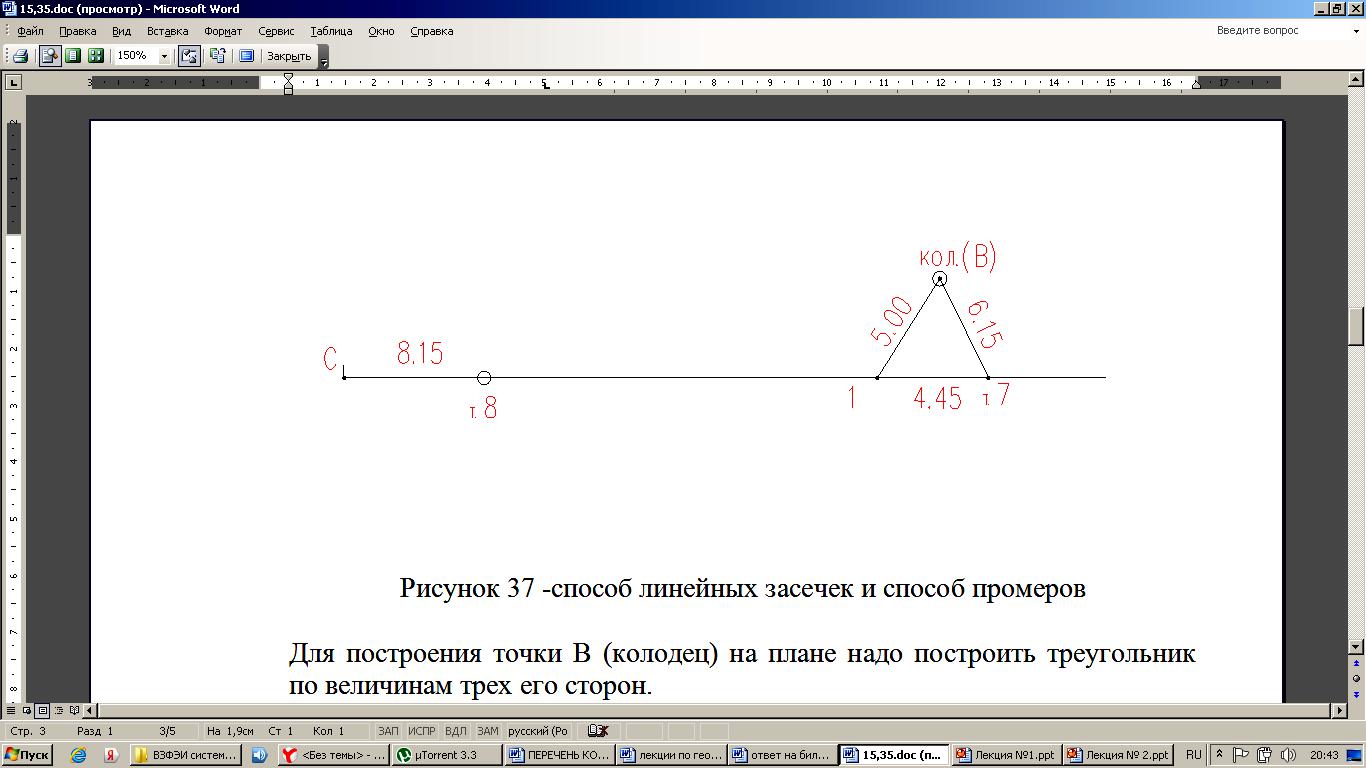 Рис. 4 способ линейных засечек и способ промеров Для построения точки В (колодец) на плане надо построить треугольник по величинам трех его сторон. Применяется при съемке зданий. Основан на построении треугольника, и положение точек определяется изменением его сторон 5) Способ створов (см. выше рис. 4) -применяется при съемке точек расположенных в створе опорных линий, стен капитальных сооружений, либо сторон теодолитного хода (рисунок 4). Плановое положение точки, например, С определяется по длине отрезка от точки 8 до точки С. Применяется при съемке точек, расположенных в створе линии теодолитного хода. При съемке ситуации составляется абрис, который является схематическим чертежом, на котором показывают все снимаемые точки с соблюдением порядка и взаимного расположения контуров местности между собой и относительных опорных линий 16 Как прокладываются теодолитные ходы, их назначение? Теодолитный ход - система ломаных линий, в которой углы измеряются теодолитом. Стороны теодолитного хода, как правило, прокладываются по ровным, твёрдым и удобным для измерений местам. Их длина составляет 50—400 м, угол наклона до 5°. Вершины углов теодолитного хода закрепляют временными и постоянными знаками. Съёмка подробностей проводится с опорных точек и линий теодолитного хода, который прокладывается между опорными пунктами триангуляции, полигонометрии или образуется в виде замкнутых полигонов (многоугольников). Качество пройденного теодолитного хода определяется в ходе сопоставления фактических ошибок с допустимыми. Погрешность измерения углов в теодолитном ходе обычно не превышает 1'; а сторон — 1:2000 доли их длины. Обычно теодолитная съемка применяется для создания контурных планов небольших по размеру участков местности. 17. Обработка полевых материалов теодолитной съемки. Первичную обработку результатов линейных и угловых измерений (нулевой контроль и оценку их пригодности для последующих вычислений), выполняют непосредственно в полевых журналах. При первичной обработке находят среднее значение из ряда измерений одной и той же величины, определяют допустимость отклонений, делают повторные вычисления (выполняет другой специалист). Основную обработку результатов измерений в теодолитном ходе выполняют после полевого контроля и записывают на бланках-ведомостях. Исходные данные для обработки: горизонтальные углы, длины сторон, дирекционный угол примычной стороны и координаты точек государственной геодезической сети, к которым привязывают теодолитный ход. 18. Формула для вычислений дирекционных углов в теодолитном ходе. Дирекционным углом α называется, горизонтальный угол между направлением данной линии и северной частью осевого меридиана или линии, ему параллельной, отсчитываемый по ходу часовой стрелки. Обозначается α, изменяется в пределах от 0° до 90°. где n+1 – дирекционный угол последующей стороны; n+1 – дирекционный угол предыдущей стороны; испр – исправленный, вправо по ходу лежащий угол. При вычислении, если n +180< испр, то необходимо прибавить 3600. Если n+1 = n+ 180-испр >3600, то необходимо вычитать 3600. 19. Связь между дирекционными углами и румбами сторон теодолитного хода. Дирекционным углом α называется, горизонтальный угол между направлением данной линии и северной частью осевого меридиана или линии, ему параллельной, отсчитываемый по ходу часовой стрелки. Обозначается α, изменяется в пределах от 0° до 90°. Прямой и обратный дирекционные углы одной и той же линии отличаются на 1800 (рисунок 1). 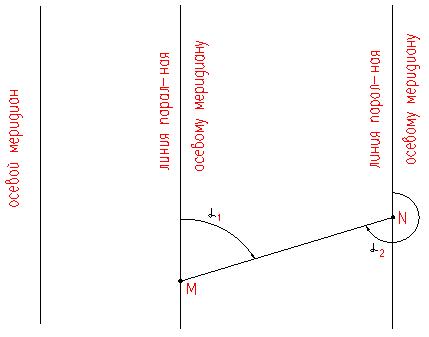 Рисунок 1- Прямой и обратный дирекционные углы Румбом называется острый горизонтальный угол отчитываемый от ближайшего конца меридиана (северного или южного) до направления на данный предмет. Румб обозначается буквой r с индексами, указывающими четверть, в которой находится румб: rСВ, rЮВ, rЮЗ, rСЗ и изменяется в пределах от 0° до 90° (рисунок 1). 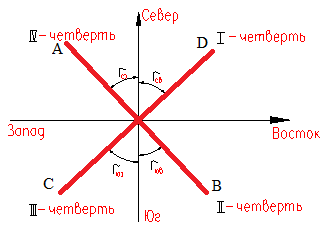 Рисунок 1- Румбы Одним из этапов вычислительной обработки теодолитного хода является вычисление румбов. Перевод дирекционных углов в румбы. Дирекционные углы переводят в румбы, пользуясь зависимостью между дирекционными углами и румбами (табл.1) Таблица 1 - Зависимость между дирекционными углами и румбами
20. Как вычисляется относительная невязка? Относительная невязка теодолитного хода ƒотн определяется как частное от деления абсолютной невязки хода ƒабс на периметр хода Р по следующей формуле: где P –периметр хода; fабс - абсолютной невязки на периметр хода/ Абсолютная невязка на периметр хода fабс определяется по следующей формуле: Допустимая относительная невзяка fдоп.отн.= 21. Как вычисляются исправленные приращения? Исправленные приращения координат рассчитываются по формуле: ∆xисп.= ∆xв. + (+- f∆xв. / n) ∆yисп.= ∆yв.+(+- f∆yв. / n) где, ∆xисп и ∆yисп. – исправленное приращения координат; ∆xв. и ∆yв. – вычисленное приращение координат; f∆xв= ∑ ∆xв; ∑ ∆xв = ∆xв1+∆xв2+…+ ∆xn; f∆yв.= ∑ ∆xв; ∑ ∆yв = ∆yв1+∆yв2+…+ ∆yn; где n – количество приращений. 22. Прямая геодезическая задача. В геодезии часто приходится передавать координаты с одной точки на другую. Зная исходные координаты данной точки, горизонтальное расстояние ее до другой и направление линии, соединяющей обе точки (азимут, дирекционный угол, или румб), можно определить координаты второй точки. Такая задача называется прямой геодезической задачей. На плоскости она решается следующим образом (рисунок). 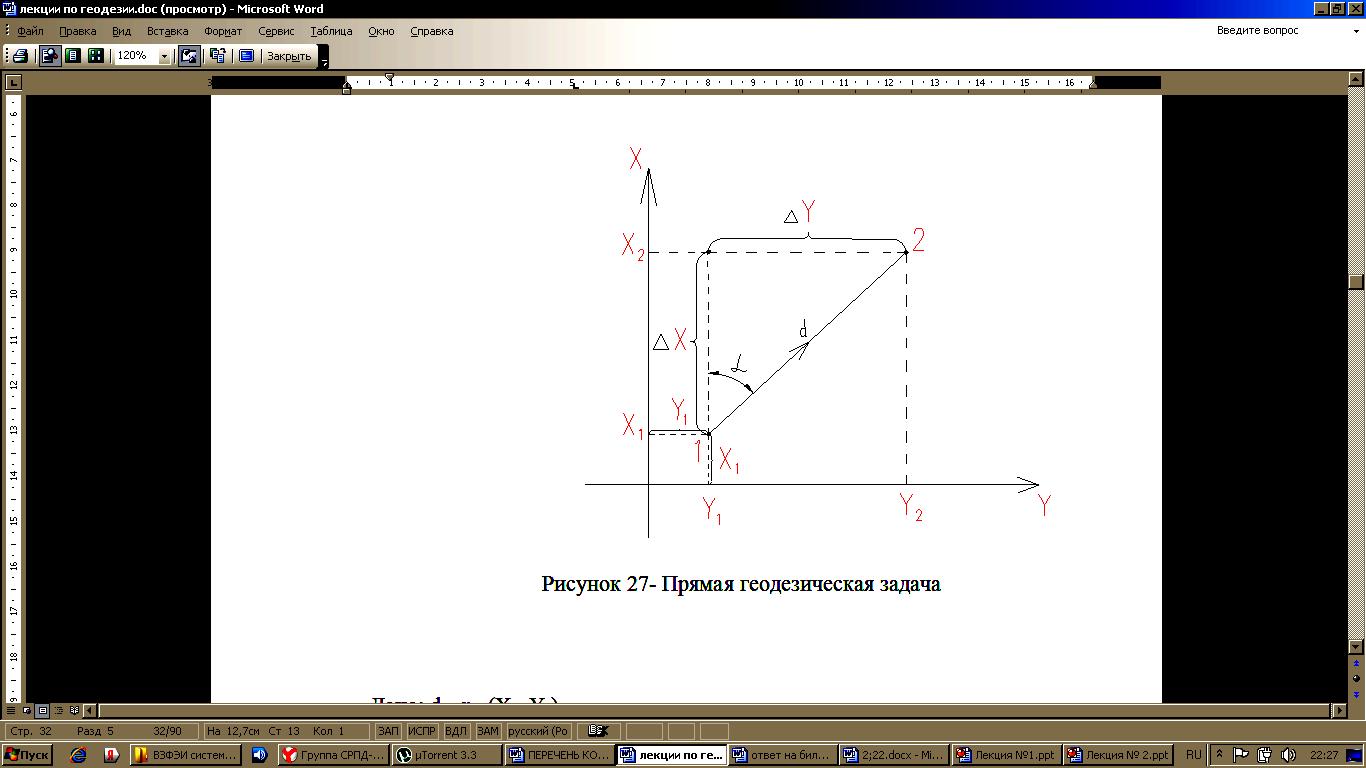 Прямая геодезическая задача Дано: d , α , (X1, Y1) Определить: (X2, Y2) Решение: X2 = X1 + Δ X Y2 = Y1 + Δ Y ± Δ X = d * cos α ± Δ Y = d *sin α Δ X и Δ Y - приращение координат. Знак Δ x и Δ y зависят от знаков cos α и sin α. Таким образом, если мы имеем на местности ряд смежных треугольников, измерив все углы треугольников и одну из сторон, можно вычислить все остальные элементы треугольников. С помощью прямой геодезической задачи определяются координаты всех вершин треугольников. 23. Определение превышений тригонометрическим нивелированием (применяемые приборы) и назначение. Нивелирование – вид геодезических измерений, в результате которых определяют превышения точек, а так же их высоты над принятой уровенной поверхностью. Нивелиры по строению бывают: - оптические; - лазерные; - цифровые. Для определение превышения между точками А и В (рисунок 1), в точках устанавливают отвесно рейки, а по середине между ними прибор – нивелир. С помощью нивелира берут отчеты а и в, которые соответствуют расстояниям от низа рейки до горизонтального луча, задаваемого нивелиром, превышение будет равно h= а-в. 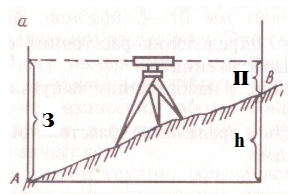 Рис. 1. Определение превышения По точности невилиры классифицируются на: Высокоточные предназначены для нивелирования I и II классов в государственных геодезических сетях, на геодезических полигонах и при ответственных инженерно-геодезических работах. Точные предназначены для нивелирования III и IV класса и инженерно-геодезических изысканий. Технические предназначены для обоснования топографических съемок, инженерно-геодезических изысканий, строительства. Электронные (цифровые) - это современные многофункциональные геодезические приборы, совмещающие функции: -высокоточного оптического нивелира, -электронного запоминающего устройства, -встроенного программного обеспечения для обработки полученных измерений. Выделяют следующие виды угломерных приборов (теодолитов), с помощью которых измеряют горизонтальные и вертикальные углы: - механический (с металлическим лимбом); - оптические; - электронные; - лазерные. При тригонометрическом нивелировании (рисунок 2) над точкой 1 устанавливают теодолит и измеряют высоту прибора i, а в точке 2 устанавливают рейку. Для определения превышения h измеряют угол наклона, горизонтальное проложение d и фиксируют высоту визирования (отчет, на который наведен визирный луч). 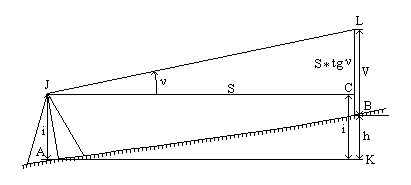 Рис.2. Тригонометрическое нивелирование Превышение вычисляют по формуле: h = ½ D·sin2ν + i – V. |
