ОТВЕТЫ ДЛЯ ЭКЗАМЕНА ПО МОС. 1 Приближенные вычисления. Соотношение между угловой и радиальной мерами измерения углов и длинами дуг
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
38.Вычисление элементов эллипса погрешности при ОМС по 2-м навигационным параметрам. Элементы среднего квадратического эллипса погрешностей также выражаются через коэффициенты нормальных уравнений и рассчитывают ся по следующим формулам: 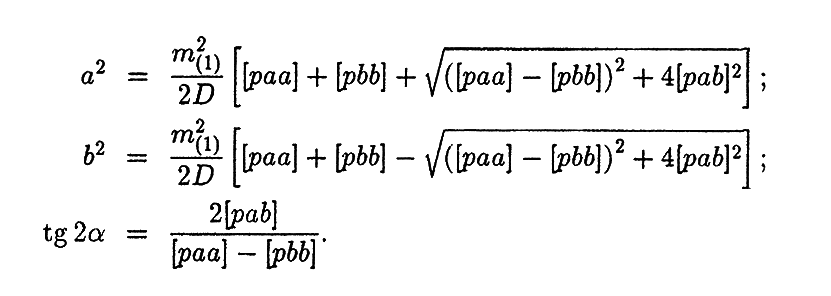 Если
Расчёт радиальной средней квадратической погрешности места судна производится по формуле  . .40)Общие принципы обработки косвенных измерений по методу наименьших квадратов. В случаях, когда искомые величины(координаты судна, коэффициенты) непосредственно не измеряют, а определяют по измерениям других, связанных с ними величин(нав. Параметры),то такие определения называются косвенными и чаще всего встречаются в судовождении.Приведение невязок таких определений в формальное согласие называют уравнением косвенных определений. Для общности и краткости записи в уравнениях поправок принято обозначать первыми буквами латинского алфавита коэффициенты при неизвестных, а последними буквами алф.-сами неизвестные:а=g*cosτ; b=g*sinτ; x=дельтаφ;y=дельтаw;L=дельтаU; L-свободные члены.Получим уравнение поправок:a*x+b*y+c*z+L=v. Свободный членL-это разность между измеренным и вычисленными значениями измеряемой величины.В L входит вся ошибка измерений. 41)Составление нормальных уравнений и способы их решений. . Составление и решение нормальных уравнений 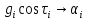 ; ;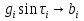 ; ;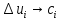 . .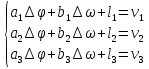 . ; . ;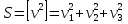 . . 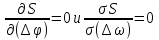 . Тогда, . Тогда,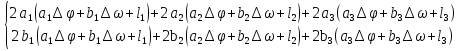 . .Выполнив сложение, получаем систему 2-х нормальных уравнений в обозначениях Гаусса: [aa]Δφ+[ab]Δω+[al]=0 [ab]Δφ+[bb]Δω+[bl]=0 Так как ui=aiΔφ+biΔω+li, то [au]=0 [bu]=0 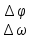 = = 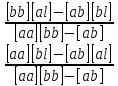 = = 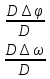 Таким образом получено правило Крамера, где D-главный определитель системы, а DΔφи DΔω- определители для Δφ и Δω соответственно.Контроль правильности решения получают подстановкой найденных неизвестных в так называемое суммарное уравнение, полученное суммированием нормальных уравнений.([aa]+[ab])Δφ+([ab]+[bb])Δω+([al]+[bl])=0 (22) Способ решения нормальных уравнений по правилу Крамера при n>2 становится трудоёмким и не всегда устойчивым при малых значениях D. Другими способами решения системы нормальных уравнений являются: -способ последовательного исключения искомых величин;-способ последовательных приближений (итерации. Первый из них применяется главным образом при неавтоматизированных вычислениях, осуществляемых в ручную или на каркуляторах. Все расчеты выполняются в специальных схемах. Наиболее употребима схема Гаусса-Зейделя, в которой вычисления сводятся к простым однообразным действиям , предусмотрены постоянный контроль правильности вычислений и оценивание точности полученных результатов.Способ итерации легко реализуется на ЭВМ , к недостатку стоит отнести итерационную процедуру, которая не даёт конечного решения, но быстродействие современных ЭВМ снимает этот вопрос. 42.Центрографический способ отыскания вероятнейшего места судна. 1. Снять с карты расстояния до ориентиров Da Db и Dc обозначив Dа наибольшее расстояние. 2. Измерить стороны треугольника а, Ь, с. 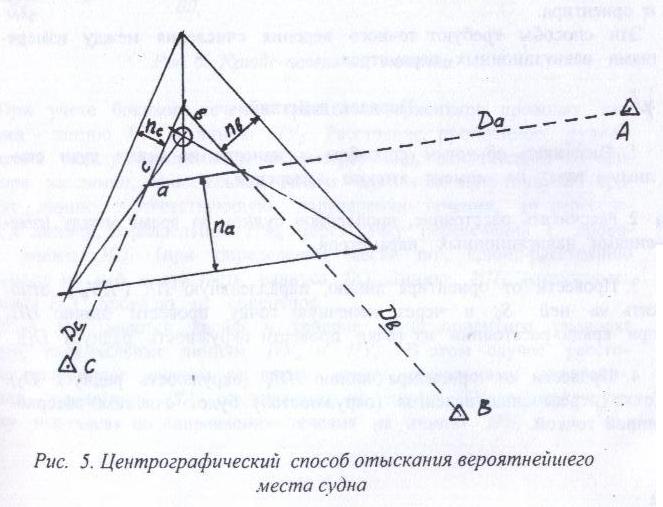 3. Рассчитать коэффициенты: 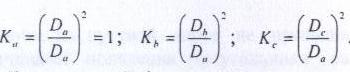 4. Рассчитать переносы: nа = Ка*а; nb = Kb*b; nс = Кс*с 5. Провести линии, параллельные сторонам треугольника, на рас-расстояниях от них, равным переносам. 6. Провести линии через сходственные углы треугольника по-погрешностей и полученного внешнего треугольника. Точка пересечения линий будет вероятнейшим местом судна. |
