ОТВЕТЫ ДЛЯ ЭКЗАМЕНА ПО МОС. 1 Приближенные вычисления. Соотношение между угловой и радиальной мерами измерения углов и длинами дуг

• Название: 1 Приближенные вычисления. Соотношение между угловой и радиальной мерами измерения углов и длинами дуг
• Анкор: ОТВЕТЫ ДЛЯ ЭКЗАМЕНА ПО МОС.docx
• Дата: 23.10.2017
• Размер: 0.95 Mb.
• Имя файла: ОТВЕТЫ ДЛЯ ЭКЗАМЕНА ПО МОС.docx
• Тип: Документы; #9711
• страница: 1 из 3

1)Приближенные вычисления. Соотношение между угловой и радиальной мерами измерения углов и длинами дуг.

Приближённые вычисления, вычисления, в которых данные и результат (или по крайней мере только результат) являются числами, лишь приближённо представляющими истинные значения соответствующих величин. П. в. возникают в связи с численным решением задач и обусловлены неточностями, которые присущи формулировке задачи и способам её решения. Общие правила и теорию методов П. в. принято называть численными методами.Обозначение единиц измерения плоского угла:

градус- «°»;минута - «’»;секунда - «"».

Соотношение между угловыми единицами:

1° = 1/360 полного оборота = 2Π/З60 рад = 0,017453 рад;

1’ = 1/60° = Π/108*10^-2 рад = 0,000 291 рад;1’’ = 1/60’’ = Π/648*10^-3 рад = 0,000 005 рад.
2)Тригонометрические функции малых углов.

Пусть a будет какой-нибудь острый угол. Возьмём на одной из его сторон произвольную точку и опустим из неё перпендикуляр на другую сторону угла. Тогда мы получим прямоугольный треугольник. Возьмём отношения сторон этого треугольника попарно, а именно:1) отношение катета, противолежащего углу, к гипотенузе,

2) отношение катета, прилежащего углу, к гипотенузе,

3) отношение катета, противолежащего углу, к катету прилежащему,и обратные им отношения.

Величина каждого из этих отношений не зависит от положения точки на стороне угла.Все указанные отношения называются тригонометрическими функциями. Чаще других отношений берутся следующие четыре:

1) отношение катета, противолежащего углу a, к гипотенузе называется синусом угла a и обозначается sin(a),2) отношение катета, прилежащего углу a, к гипотенузе называется косинусом угла a и обозначается соs(a),3) отношение катета, противолежащего углу a, к катету прилежащему называется тангенсом угла a и обозначается tg(a),4) отношение катета, прилежащего углу a, к катету противолежащему называется котангенсом угла a и обозначается сtg(a).Так как каждый из двух катетов меньше гипотенузы, то синус и косинус каждого угла есть число меньшее единицы. Зависимости между тригонометрическими функциями одного и того же угла. Простейшие из этих зависимостей следующие четыре: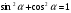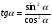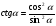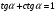

;;;
3)Элементы сферической тригонометрии

Сферическая тригонометрия занимается изучением соотношений между сторонами и углами сферических треугольников (например, на поверхности Земли и на небесной сфере).Сферические треугольники. На поверхности шара кратчайшее расстояние между двумя точками измеряется вдоль окружности большого круга, т. е. окружности, плоскость которой проходит через центр шара. Вершины сферического треугольника являются точками пересечения трех лучей, выходящих из центра шара и сферической поверхности. Сторонами a, b, c сферического треугольника называют те углы между лучами, которые меньше 180 (если один из этих углов равен 180, то сферический треугольник вырождается в полуокружность большого круга). Каждой стороне треугольника соответствует дуга большого круга на поверхности шара (см. рисунок).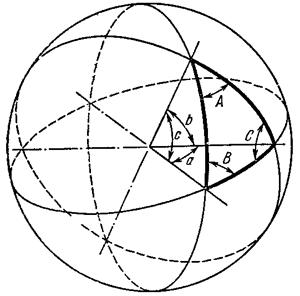



Углы A, B, C сферического треугольника, противолежащие сторонам a, b, c соответственно, представляют собой, по определению, меньшие, чем 180, углы между дугами больших кругов, соответствующими сторонам треугольника, или углы между плоскостями, определяемыми данными лучами.Геометрия на поверхности шара является неевклидовой; в каждом сферическом треугольнике сумма сторон заключена между 0 и 360, сумма углов заключена между 180 и 540. В каждом сферическом треугольнике против большей стороны лежит больший угол. Сумма любых двух сторон больше третьей стороны, сумма любых двух углов меньше, чем 180 плюс третий угол.Сферический треугольник единственным образом определяется (с точностью до преобразования симметрии):1) тремя сторонами, 2) тремя углами, 3) двумя сторонами и заключенным между ними углом, 4) стороной и двумя прилежащими к ней углами.
4)Формула косинуса стороны.

Формула косинуса стороны связывает три стороны и один из углов сферического треугольника. Удобна для нахождения неизвестного угла или стороны, противолежащей этому углу, и читается следующим образом: «в сферическом треугольнике косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов этих сторон на косинус угла между ними»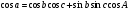


5)Формула косинуса угла и синусов

Формула косинуса угла связывает три угла и сторону сферического треугольника, удобна для нахождения неизвестной стороны или угла, противолежащего этой стороне, и читается так: «косинус угла сферического треугольника равен отрицательному произведению косинусов двух других углов плюс произведение синусов этих углов на косинус стороны между ними».;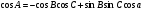

С*sinA=a*sinc;
6)Формулы пяти элементов и котангенсов.

Формула котангенсов (4-х рядом лежащих элементов) связывает 4 рядом лежащих элемента, используется для нахождения крайних элементов и читается следующим образом: "произведение котангенса крайнего угла на синус среднего угла равно произведению котангенса крайней стороны на синус средней стороны минус произведение косинусов средних элементов ".

ctg A*sinC=ctg a*sin b-cos b *cos C.
7) Решение прямоугольных сферических треугольников. Правило Модюи-Непера. Дополнительные формулы для решение косоугольных сферических треугольников.

Прямоугольным называется такой сферический треугольник, у которого один из углов равен 90°. Прямоугольные сферические треугольники более рационально решать по правилам Модюи-Непера:в прямоугольном сферическом треугольнике косинус любого среднего элемента равен произведению котангенсов крайних смежных с ним элементов; косинус отдельно лежащего элемента сферического треугольника равен произведению синусов двух не смежных с ним рядом лежащих элементов. Примечание: в обоих правилах принято, что катеты лежат рядом друг с другом и что вместо катетов надо брать их дополнения до 90°, изменяя соответственно наименования тригонометрических функций.




8)Фигура и размеры Земли.

Земля представляет собой неправильной формы шар. Длина его экваториального радиуса равна 6 378 245 м. а полярного—6 356 863 м. Как видно, экваториальный диаметр Земли длиннее полярного примерно на 42,8 км. Если изобразить отклонение формы Земли от шара на глобусе с поперечником в 1 м по экватору, то его полярная ось будет короче экваториальной на 3,35 мм. Фигура Земли имеет форму геоида, что переводится как «землеподобный». Геоидом называется фигура, ограничивающая невозмущённую поверхность уровня мирового океана, мысленно проходит под материками и островами, таким образом, что она в каждой своей точке перпендикулярна отвесной линии и имеющая неправильную геометрическую форму. Геометрия геоида очень сложна, поэтому вместо геоида при решении штурманских задач используют более простые модели Земли: эллипсоид вращения, сферу, карту. Размеры референц-эллипсоида Красовского: большая полуось а=6378245 м; в=6356863 м; полярное сжатие а=(а-в)/а=1/298,3; эксцентриситет е=0,0818;R=6371110м.
9)Основные элементы на поверхности небесной сферы и земного сфероида.

Плоскость истинного меридиана наблюдателя пересекается с плоскостью истинного горизонта по линии N — S, которая называется полуденной линией, так как в этой плоскости Солнце бывает точно в полдень.

Вертикальную плоскость, проходящую через глаз наблюдателя перпендикулярно плоскости истинного меридиана наблюдателя, называют плоскостью первого вертикала (плоскость 3). Она пересекается с плоскостью истинного горизонта наблюдателя по линии Ost—W. Таким образом, пересечение взаимно перпендикулярных плоскостей истинного меридиана наблюдателя и первого вертикала дает четыре главные линии на плоскости истинного горизонта наблюдателя, которые указывают на главные точки горизонта: N, S, Ost и W. Если наблюдатель станет лицом к северу, то за спиной у него будет юг, справа—восток, слева—запад. Линии N—S, Ost—W в любой точке земной поверхности (кроме полюсов) занимают вполне определенное положение. Направления N, S, Ost и W называют главными направлениями, или главными румбами, которые делят истинный горизонт на четыре четверти: NOst— северо-восточную, SOst — юго-восточную, SW—юго-западную и NW—северозападную. Каждая четверть делится на 8 румбов, а весь горизонт—на 32 румба.Основные географические точки, линии и круги на земном шаре.Земля непрерывно вращается в направлении с запада на восток. Диаметр, вокруг которого происходит это вращение, называется осью вращения Земли.Земля непрерывно вращается в направлении с запада на восток. Диаметр, вокруг которого происходит это вращение, называется осью вращения Земли.


Эта ось пересекается с поверхностью Земли в двух точках, которые называются географическими полюсами: один Северным (С), а другой Южным (Ю). Северным называется тот полюс, в котором, если смотреть на него сверху, вращение Земли направлено против хода часовой стрелки. Противоположный полюс называется Южным.

Через любую точку на земном шаре можно провести бесчисленное множество больших и малых кругов.Большим называется круг, образованный на земной поверхности плоскостью сечения, проходящей через центр Земли. Малым называется круг, образованный на земной поверхности плоскостью сечения, не проходящей через центр Земли. Большой круг, плоскость которого перпендикулярна оси вращения Земли, называется экватором. Экватор делит земной шар на Северное и Южное полушария. Малый круг, плоскость которого параллельна плоскости экватора, называется параллелью. Через каждую точку на земной поверхности можно провести только, одну параллель, которая называется параллелью места. Большой круг, проходящий через полюсы Земли, называется географическим, или истинным меридианом. Через каждую точку на земной поверхности, кроме полюсов, можно провести только один меридиан, который называется меридианом места. Меридиан, проходящий через Гринвичскую астрономическую обсерваторию, находящуюся в Англии вблизи Лондона, принят по международному соглашению в качестве начального меридиана.Начальный меридиан делит земной шар на Восточное и Западное полушария. Плоскость экватора и плоскость начального меридиана являются основными плоскостями, от которых производится отсчет географических координат.
10)Системы координат

Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющий положение конкретной точки, называется координатами этой точки.В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.В географии координаты — широта, долгота и высота над известным общим уровнем (например, океана). Смотри географические координаты.В астрономии координаты — величины, при помощи которых определяется положение звезды, например, прямое восхождение и склонение.Небесные координаты — числа, с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой систему полярных координат на сфере с соответствующим образом выбранным полюсом. Систему небесных координат задают большим кругом небесной сферы (или его полюсом, отстоящим на 90° от любой точки этого круга) с указанием на нём начальной точки отсчёта одной из координат. В зависимости от выбора этого круга системы небесных координат называлась горизонтальной, экваториальной, эклиптической и галактической.Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае.

11)Радиусы кривизны параллели, меридиана и нормального сечения.

Через произвольную точку на поверхности земного эллипсоида можно провести бесчисленное множество вертикальных плоскостей, которые образуют с поверхностью эллипсоида нормальные сечения. Два из них: меридианное и перпендикулярное ему сечение первого вертикала — носят название главных нормальных сечений. Кривизна поверхности земного эллипсоида в разных ее точках различна. Более того, в одной и той же точке все нормальные сечения имеют разную кривизну. Радиусы кривизны главных нормальных сечений в данной точке являются экстремальными, т. е. наибольшими и наименьшими среди всех остальных радиусов кривизны нормальных сечений. Величины радиусов кривизны меридиана М и первого вертикала N в данной широте φ определяются по формулам:M = a(1-e²) / (1 - e²*sin² φ)^3/2; N = a / (1 - e²*sin² φ)^½

Радиус кривизны r произвольной параллели эллипсоида связан с радиусом кривизны сечения первого вертикала соотношением r = N cos φ .Величины радиусов кривизны главных сечений эллипсоида М и N характеризуют его форму вблизи данной точки. Для произвольной точки поверхности эллипсоида отношение радиусов

M / N = 1 - e² / 1 - e²*sin² φ

12)Длина дуг параллели и меридианов.

Зная радиус Земли, можно рассчитать длину большого круга (меридиана и экватора);

L = 2pR = 2. 3,14 • 6371 »40000 км.

Определив длину большого круга, можно найти длину дуги меридиана (экватора) в 1° или в 1¢:1° дуги меридиана (экватора) = L/360°= 111 км,1¢ дуги меридиана (экватора) 111/60¢ = 1,853 км.Длина каждой параллели меньше длины экватора и зависит от широты места.

Она равна L пар= L экв соsj пар.Положение точки на поверхности земного эллипсоида может быть определено геодезическими координатами - геодезической широтой и геодезической долготой. Для определения положения точки на поверхности геоида используются астрономические координаты, получаемые путем математической обработки результатов астрономических измерений. Однако в ряде случаев, когда не нужно учитывать разности геодезических и астрономических координат, для определения положения точки в самолетовождении пользуются понятием географические координаты .Географической широтой j называется угол между плоскостью экватора и нормалью к поверхности эллипсоида в данной точке. Широта измеряется от плоскости экватора к полюсам от 0 до 90° к северу или югу. Северная широта считается положительной, южная - отрицательной.

13)Преобразование координат.

Преобразованием системы координат называется переход от одной системы координат к другой.При такой замене надо установить формулы, позволяющие по известным координатам точки в одной системе координат определить ее координаты в другой.

Главной целью преобразования координат является определение такой координатной системы, в которой уравнение данной линии становится наиболее простым. Удачным расположением координатных осей можно добиться того, чтобы уравнение кривой приняло наиболее простой вид. Это имеет важное значение для исследования свойств кривой.
14)Геодезическая линия. Прямая и обратная геодезическая задача.

Геодезическая линия, кривая, главные нормали всех точек которой совпадают с нормалями поверхности, на которой та расположена. Кратчайшее расстояние между двумя точками по поверхности - Г. линия, но не всегда обратно.Геодезическая задача, связана с определением взаимного положения точек земной поверхности и подразделяется на прямую и обратную задачу. Прямой Г. з. называют вычисление геодезических координат — широты и долготы некоторой точки, лежащей на земном эллипсоиде, по координатам др. точки и по длине и азимуту геодезической линии, соединяющей эти точки. Обратная Г. з. заключается в определении по геодезическим координатам двух точек на земном эллипсоиде длины и азимута геодезической линии между этими точками
15)Сближение меридианов.Сближение меридианов в некоторой точке земного эллипсоида — угол g^s между касательной к меридиану этой точки и касательной к эллипсоиду, проведённой в той же точке параллельно плоскости некоторого начального меридиана. С. м. g^s является функцией разности долгот l указанных меридианов, широты В точки и параметров эллипсоида. Приближённо С. м. выражается формулой g^s = lsin В. С. м. на плоскости геодезической проекции, или картографической проекции (или гауссово С. м.) — это угол g, который образует касательная к изображению какого-либо меридиана с первой координатной осью (абсцисс) данной проекции, являющейся обычно изображением среднего (осевого) меридиана отображаемой территории.
16)Общий принцип изображения поверхностей развёртыванием.

РАзвертыванием одной поверхности на другую при помощи изгибания называется такое преобразование первой поверхности, при котором сохраняются элементы её внутренней геометрии.т.е углы . ПЛОЩАДИ, гАУССОВА кривизна поверхности, а так св-во кратчайших линий оставаться кратчайшими.Радиусы кривизны гл. нормальных сечений называются гл. радиусами кривизны в данной точке поверхности..R=1/R1*R2- гауссовая кривизна поверхности
17)Предмет и произведения картографии.

Картография – наука о географических картах, о методах их создания и использования.

По объекту: Земное (Суша, море), астрономическое, Планетное.По тематике: Географическое, Тематическая (природа, общество), Специальное.По методу: Наземное, Аэрокосмическое, Подводное.По масштабу: Крупное, мелкое, Среднее. В судовождении Планы (1:50000 и крупнее) Пуиевые (1:100000 – 1:500000) Генеральные (1:1000000 и меньше).Планом называется такое изображение земн пов, искажение которой не выходит за географической точности Предельная точность масштаба длина линии на местности соответствующая длине отрезка на плане.
18)Масштабы.Масштабом называется отношение длины линии на плане или карте к соответствующей проекции этой линии на местности.Масштабы на картах и планах могут быть представлены численно или графически.Численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1:5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности.Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1:1 000 крупнее, чем масштаб 1:25 000.Графические масштабы подразделяются на линейные и поперечные. Линейный масштаб — это графический масштаб в виде масштабной линейки, разделённой на равные части. Поперечный масштаб — это графический масштаб в виде номограммы, построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла.Точность масштаба — это отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м), 0,1 мм — 100 см (1 м).В судовождении Планы (1:50000 и крупнее) Пуиевые (1:100000 – 1:500000) Генеральные (1:1000000 и меньше). Главный масштаб это отношение показывающее во сколько раз уменьшены размеры сфероида при переносе его на карту
19)Классификация картографических сеток и способы их построения.

Картографическая сетка, графическое изображение на плоскости (карте) географических меридианов и параллелей. При составлении географических карт К. с. служит для построения картографического изображения. При пользовании картой К. С. позволяет определять координаты любой точки (географические или прямоугольные, в зависимости от вида К. с.) и азимуты линий, а также судить о величине искажений картографической проекции в различных частях карты .Есть Нормальная, Поперечная и Косая сетки.
20)Классификация картографических проекции и основные требования к морской навигационной карте.Все картографические проекции классифицируют по двум признакам:по характеру искажений; по виду нормальной картографической сетки.По характеру искажений проекции делятся на:равновеликие ,равноугольные ,Равнопромежуточные, Произвольные.В равновеликих проекциях сохраняется неизменным масштаб площадей (т. е. отношение бесконечно малой площади на карте к соответствующей площади на местности). При этом масштабы по главным направлениям отвечают условию aּb=const. У них нарушается подобие фигур, искажаются направления и углы.В равнугольных проекциях сохраняется подобие бесконечно малых фигур. Частные масштабы по всем направлениям в каждой данной точке карты у них одинаковы – m=n=const. Углы на карте у таких проекций равны соответствующим углам на местности. Однако у них искажены соотношения площадей.В равнопромежуточных проекциях сохраняется неизменным масштаб длин по одному из главных направлений – a=const или b=const.Все остальные проекции относятся к произвольным.По виду нормальной картографической сетки проекции делятся на:цилиндрические ,конические ,азимутальные ,псевдоцилиндрические ,псевдоконические ,псевдоазимутальные, поликонические ,круговые ,производные.В цилиндрических проекциях меридианы и параллели нормальной сетки изображаются в виде двух систем параллельных прямых пересекающихся под углом 90°.Вид функции f(φ) и величина параметра проекции α определяют характер искажений. Цилиндрические проекции могут быть равноугольными, равновеликими и равнопромежуточными. В зависимости от вида картографической сетки, они могут быть нормальными, косыми и поперечными. Равноугольная нормальная, а при плавании в высоких широтах поперечная цилиндрическая проекции являются основными для составления МНК.В конических проекциях параллели нормальной картографической сетки изображаются в виде двух концентрических окружностей, а меридианы в виде их радиусов, причем углы между ними пропорциональны соответствующим разностям долгот.Также как и цилиндрические, конические проекции могут быть равноугольными, равновеликими и равнопромежуточными, а также нормальными, косыми и поперечными. Они используются для изобржения большого района океана, а также для составления аэронавигационных карт (1:1 000 000 и мельче).В азимутальных проекциях параллели нормальной картографической сетки изображаются в виде концентрических окружностей, а меридианы – их радиусами, причем углы между ними равны соответствующим разностям долгот.Из класса Азимутальных выделяются перспективные,Гномоническа,Стереографическая,Внешняя,Ортографическая.Основные требования к морским навигационным картам.1)Локсодромия должна изображаться прямой линией.2)Проекция должна быть равноугольная.
21)Принцип плавания заданным маршрутом. Виды изолиний.

Изолиния – геометрическое место точек, отвечающее постоянному навигационному параметру U. U=F(φ ; λ) – уравнение изолинии в общем виде.Виды изолиний.

Изолиния пеленга. (линия равных пеленгов - сферич. кривая, в каждой точке к-рой пеленг (сферич. угол или азимут) на ориентир (маяк, радиомаяк) остается постоянным)Изолиния дистанции. (Изостадии - линии на морской карте, соединяющие точки равных расстояний от судна до некоторых ориентиров)Изогона – изолиния горизонтального угла или разности азимутов – кривая, проходящая через ориентиры и вмещающая измеренный угол α.Изолиния вертикального угла – окружность радиусом D с центром в точке B, которая обозначает расположение ориентира на карте D=h ctgβ, где h – высота ориентира. β1=β2=β3=...=const.

22)Определение места судна по изолиниям. Градиент навигационного параметра.

Определение места судна- обсервация- заключается в отыскании географических координат Ф0 лямда0 той точки, где в данный момент судно находится.
для опред. места судна по изолиниям обычно применяется, когда изолинии параметров имеют простую форму.при пеленговании двух ориентиров графическое решение выполняется так:ПРОИЗВЕДЯ ИЗМЕРЕНИЯ И обработав из результ, находят величинв пеленгов П1 иП2 ориентиров, на карте прокладывают от ориентиров изолинии пеленгов в виде отрезков прямых, в точке пересечения изолиний находят обсервованное место судна..
Градиент-навиг. параметра- характеризут скорость изменения параметра по направлению нормали к изолинии и направлен в сторону увеличения параметра.
23)Линия положения. Уравнение линии положения.

Линией положения называется касательная (или хорда), проведенная к изолинии вблизи счислимого места и замещающая собой изолинию.

Уравнение ЛП :

24)Способы ОМС по двум линиям положения.

Способы: Аналитический:измеряются навигационные параметры,по замеченным в период измерения координатам, определяем значение счислимых параметров счислимой точки.Вычисляем приращение навигационного параметра,определяем модули градиентов и направление градиентов,рассчитываем перенос линии положения,составляем простые уравнения линий положения и вычисляем разность широт и отшествие по определителям 2 порядка.





















25)Градиенты навигационного параметра.

Любые измерения содержат ошибки, поэтому измерив пеленг, дистанцию или угол и проложив на карте соответствующую изолинию, нельзя считать, что судно будет находиться на этой изолинии. Вычислить возможное смещение изолинии из-за ошибок наблюдений можно, используя понятие градиента функции.

Изобразим две изолинии, соответствующие значениям навигационных параметров U и U + ∆U (рис. 8.2). На всей изолинии значение функции навигационного параметра остается постоянным, но оно изменится при переходе на другую изолинию. Чем теснее расположены изолинии друг к другу, тем меньше расстояние ∆n между ними при заданном приращении функции ∆U, тем быстрее меняется функция в данном районе. Это изменение удобно характеризовать отношением ∆U/∆n или вектором g, направленным в сторону возрастания функции по нормали к изолинии. Вектор g называется градиентом. Таким образом, градиентом навигационного параметра назы­вается вектор, направленный по нормали к навигационной изолинии в сторону ее смещения при положительном приращении параметра, причем модуль этого вектора характеризует наибольшую скорость изменения па­раметра в данном месте. Этот модуль равен


Размерность модуля градиента равна размерности параметра U на линейную величину. Направления вектора градиента и линии положения взаимно перпендикулярны, обозначается направление градиента символом r.

Если при измерении навигационного параметра U допущена ошибка ∆U и известен градиент, то смещение линии положения параллельно самой себе определяется формулой



Чем больше величина градиента g, тем меньше смещение линии положения при той же ошибке ∆U, тем точнее будет определение места судна.
26)Основные понятия и определения теории вероятности. Законы распределения случайных величин.

Частное определение: отношение числа случаев появления события A(m) к общему числу проведённых испытаний (n).Классическое определение: отношение числа испытаний благоприятных событию A(m) к общему числу испытаний (n).Косвенное определение вероятности: в этом случае сложные события разбиваются на несколько простых, вероятность которых подсчитывается частными или классическими, затем вероятность сложного события определяется по вероятностям составляющих его простых событий с использованием теорем сложения и умножения вероятностей.Случайные величины и законы их распределения (СВ):Дискретные: происходят через определённый интервал времени.Непрерывные: непрерывные события.Самый распространенный и наиболее общим законом распределения случайной величины при неограниченном количестве измерений наз-ся закон Гаусса.

27)Числовые характеристики случайных величин и случайных функций.

Случайной величиной называется такая величина, которая в результате опыта может принимать различные заранее не известные численные значения при сохранении определенной совокупности условий, сопровождающий данный опыт. Одни случайные величины могут принимать отдельные друг от друга изолированные числовые значения. Такие случайные величины называются дискретными или прерывными.

Числовые характеристики случайных величин. 1)Математическое ожидание (среднее значение).Определение:

Математическим ожиданием называется- для дискретной случайной величины:

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания) - для непрерывной случайной величины:Интеграл должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания).Свойства математического ожидания:a . Если С - постоянная величина, то МС = С, b . МСх = СМх, c . Математическое ожидание суммы случайных величин всегда равно сумме их математических ожиданий: М(х+y) = Мх + Мy, d . Вводится понятие условного математического ожидания. Если случайная величина принимает свои значения хi с различными вероятностями p(xi/Hj) при разных условиях Hj, то условное математическое ожидание определяется как

или Если известны вероятности событий Hj, может быть найдено полное математическое ожидание:

Если f(x) - есть функция случайной величины х, то определено понятие математического ожидания функции случайной величины: - для дискретной случайной величины:

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся.

-для непрерывной случайной величины: Интеграл должен быть абсолютно сходящимся. 2 . Дисперсия случайной величины. Определение:

Дисперсией случайной величины х называется математическое ожидание квадрата отклонения значения величины от ее математического ожидания: Dx = M(x-Mx)2 - для дискретной случайной величины:

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)- для непрерывной случайной величины:

Интеграл должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии) .Свойства дисперсии:a . Если С - постоянная величина, то DС = 0, b . DСх = С2Dх, c . Дисперсия суммы случайных величин всегда равно сумме их дисперсий только, если эти величины независимы (определение независимых величин), d . Для вычисления дисперсии удобно использовать формулу: Dx = Mx2 - (Mx)2
28)Измерения и наблюдения. Классификация измерения.Дискретные – это такие измерения которые выполняются через определённый интервал времени.Непрерывные – это те измерения которые ведутся всегда автоматизированными аппаратами.Необходимые – это измерения минимальное количество которых обеспечивает.Избыточные – это такие которые выполнены сверх необходимых.Равноточные – это такие СКП результат измерения которых будет одинаковый.По степени взаимо связи:взаимонезависимы – измерение погрешности которой формируется различными факторами.корреляционновзаимозависимы – это измерения в состав погрешности которых входит одна и та же общая погрешность сформирована одним и тем же фактором.Функциональнозависимы – это измерения все погрешности которых формируются одним и тем же фактором..
29)Классификация погрешности и их свойства. Методы учёта систематических погрешностей.Погрешность измерения называется разница между измеренным и истинным значением величины.Непосредственно источник погрешности является:несовершенство приборов и инструментов,несовершенство органов чувств и не стабильность психического состояния,незакономерные колебания параметров внешней среды,нестабильность метода измерений, несовершенство метода измерений.По характеру действия на величину погрешности подразделяются на:случайные, Систематические.

систематические на: Постоянные,Переменные,периодические ,прогрессивные,грубые (промахи).

30)Нормальный закон распределения случайных погрешностей. Функция Лапласа. Распределение Стьюдента.

 Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Нормальный закон распределения также называется законом Гаусса.

            Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Нормальный закон распределения имеет плотность распределения

(*)

где m и s>0 некоторые числовые параметры. В  разделе «Предельные теоремы теории вероятностей.» будут обсуждены причины, в силу которых нормальный закон распределения играет важную

роль в теории вероятностей и ее приложениях.

х. Легко убедиться, что кривая, определяемая функцией распределения (*), имеет максимум в точке x=m, а точки перегиба отстоят от точки x=m на расстоянии s и при  функция (*) асимптотически приближается к нулю. График функции (*) изображен на рис. 9

 

 

 

 

 

                

 


В зависимости от величины параметров кривая плотности вероятности имеет различный вид и поэтому правильнее было бы говорить о семействе нормальных законов распределения (на рис. 10 показана зависимость формы кривой распределения от величины s при фиксированном m).
Нормальный закон распределения относится к непрерывной случайной величине. И тесно связан с таким понятием как функция Лапласа. Она нужна для нахождения вероятности

функции Лапласа - это вероятность того, что случайная величина примет значение, принадлежащее заданному интервалу. При решении задач по теории вероятности, как правило, требуется найти значение функции Лапласа по известному значению аргумента или, наоборот, по известному значению функции Лапласа требуется найти значение аргумента. Для этого пользуются таблицей значений функции Лапласа. Таблица значений функции Лапласа незаменима при изучении теории вероятности, так как решать интеграл (функцию Лапласа) сложно, а запомнить таблицу значений функции Лапласа просто невозможно.

Функцию Лапласа и данную таблицу чаще всего изучают на втором курсе университета, при изучении математики и теории вероятности, если Вам в данной теме, что-то не понятно, то Вы всегда можете задать вопрос на нашем форуме, мы будем рады вам помочь. Пользуйтесь нашим сайтом и таблицей на здоровье.

Функция Лапласа



При разных значениях t; F(–t) = –F(t) (функция нормального распределения).

Распределение Стьюдента

Распределе́ние Стью́дента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений. Названо в честь Уильяма Сили Госсета, который первым опубликовал работы, посвящённые распределению, под псевдонимом «Стьюдент».

Пусть  — независимые стандартные нормальные случайные величины, такие что . Тогда распределение случайной величины , где



называется распределением Стьюдента с  степенями свободы. Пишут . Её распределение абсолютно непрерывно и имеет плотность

,

где  — гамма-функция Эйлера.