Брикетировочный автомат - ТММ. 1 Проектирование основного механизма брикетировочного автомата и определение закона движения его начального звена
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
2 Силовой расчет механизма брикетировочного аппарата 2.1 Исходные данные для силового расчета Силовой расчет механизма проводится в положении 5’, угловая координата кривошипа 1 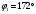 . .Моменты инерции звеньев механизма 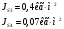 Внешние силы, действующие на звенья механизма: 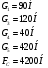 Из первого листа для положения 5’ механизма: угловая скорость 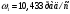 угловое ускорение 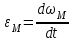 звена динамической модели, равное угловому ускорению звена динамической модели, равное угловому ускорению 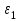 начального звена механизма (обобщенному угловому ускорению), определяется из уравнения движения в дифференциальной форме начального звена механизма (обобщенному угловому ускорению), определяется из уравнения движения в дифференциальной форме 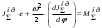 , ,полученного из уравнения Лагранжа 2-го рода, и подсчитывается по формуле 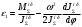 . .Производную 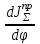 нашли графически, используя соотношение нашли графически, используя соотношение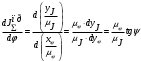 , ,где 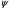 - угол между касательной, проведенной к кривой - угол между касательной, проведенной к кривой 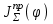 в исследуемом положении, и положительным направлением оси абсцисс. Таким образом, угловое ускорение звена 1 в положении 5’ имеет значение: в исследуемом положении, и положительным направлением оси абсцисс. Таким образом, угловое ускорение звена 1 в положении 5’ имеет значение: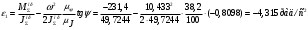 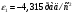 Момент сопротивления, действующий на звено 1 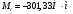 2.2 Построение плана скоростей механизма Для определения скоростей звеньев механизма необходимо построить план скоростей для заданного положения механизма. Построения представлены на листе 2. Выбранный масштаб скоростей 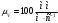 . .Скорость точки 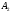 : :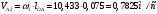 . .Для точки 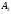 (принадлежащей звену 3): (принадлежащей звену 3):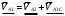 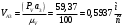 где 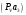 - длина отрезка - длина отрезка 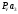 , взятого с графического листа 2 и соответствующего , взятого с графического листа 2 и соответствующего 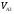 . .Построен план скоростей и из него найдены неизвестные составляющие. Для точки B (методом пропорционального деления): 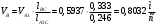 Для точки 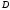 : :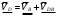 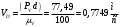 Тогда для точки 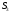 (методом пропорционального деления): (методом пропорционального деления):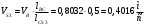 Тогда для точки 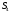 (методом пропорционального деления): (методом пропорционального деления):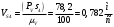 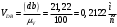 Угловая скорость третьего звена: 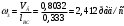 Угловая скорость четвертого звена: 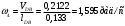 2.3 Построение плана ускорений механизма Для нахождения ускорений центров масс звеньев и угловых ускорений звеньев, необходимо построить план ускорений механизма. Выбран масштаб ускорений 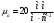 Определяем ускорение точки А второго звена: 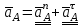 . .Нормальное ускорение точки А: 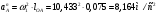 . .Тангенциальное ускорение: 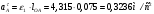 . .Полное ускорение точки А:  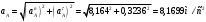 / /Ускорение точки A третьего звена: 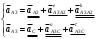 Ускорение Кориолиса для точки A третьего звена относительно второго звена: 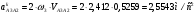 . .Нормальная составляющая ускорения точки A3 относительно точки C: 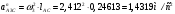 . .Ускорение точки A3 найдено из плана ускорений: 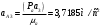 Методом пропорции найдены ускорения точек B и 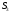 : :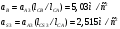 Определено ускорение точки D четвертого звена: 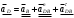 . .Нормальная составляющая ускорения точки D относительно точки B: 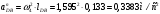 . .По плану ускорений находятся неизвестные составляющие: 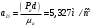 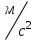 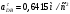 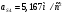 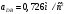 Определены угловые ускорения звеньев: 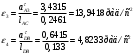 2.4 Определение сил инерции, главных моментов сил инерции Силы инерции определяются по формуле 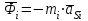 , ,откуда получено 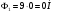 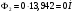 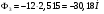 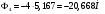 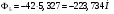 Для определения главных моментов сил инерции, воспользовались формулой 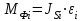 . .Для звеньев механизма получено 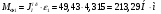 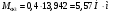 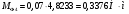 2.5 Определение реакций в кинематических парах Расчетные схемы для всех звеньев механизма, а также планы сил изображены на графическом листе 2. Для нахождения неизвестных силовых факторов воспользовались принципом Даламбера. Для всех планов сил выбран масштаб 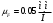 2.5.1 Группа звеньев 4-5 Сумма всех моментов относительно точки D: 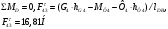 . .Сумма всех внешних сил равна 0: 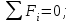 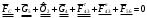 , ,Графическим способом определены величины 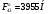 и и 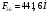 . .2.5.2 Группа звеньев 2-3 Сумма всех моментов относительно точки A: 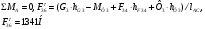 . .Сумма всех внешних сил равна 0: 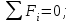 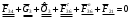 , ,Графическим способом определены величины 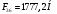 и и 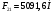 . .2.5.3 Звено 1 Записана векторная сумма всех сил, действующих на звено 1, и построен план сил: 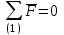 , ,Откуда 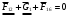 . .По плану найдена неизвестная сила реакции: 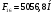 . .Сумма всех моментов относительно точки O: 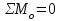 ; ; 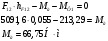 2.6 Расчет погрешности в определении движущего момента Относительная погрешность между движущими моментами, полученными на 1-м и 2-м листах проекта: 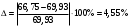 , ,Что входит в пределы допустимой погрешности. Неточность измерения движущего момента связана с тем, что в расчетах первого листа действие сил тяжести не было учтено. 3. Проектирование зубчатых механизмов. 3.1 Исходные данные для проектирования Данные для проектирования зубчатой передачи занесены в таблицу 3.1. Таблица 3.1
3.2 Геометрический расчет эвольвентной зубчатой передачи Геометрические параметры Угол профиля: 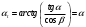 . .Шаг: 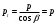 . .Модуль зубьев: 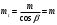 . .Коэффициент высоты головки зуба: 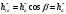 . .Коэффициент радиального зазора: 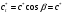 . .Радиусы делительных окружностей колес: 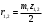 . .Радиусы основных окружностей: 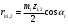 . .Суммарное смещение: 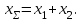 Суммарное количество зубьев: 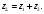 Угол зацепления передачи: 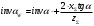 . .Межосевые расстояния 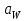 для положительной зубчатой передачи: для положительной зубчатой передачи: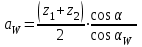 . .Делительные диаметры шестерни и колеса: 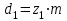 ; ; 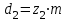 Диаметры основных окружностей: 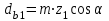 ; ; 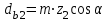 . .Начальные диаметры шестерни и колеса: 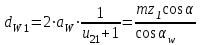 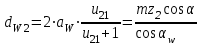 . .Коэффициенты воспринимаемого смещения: 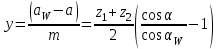 . .Коэффициент уравнительного смещения: 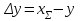 . .Исполнительные размеры зубчатых колес Диаметры вершин зубьев шестерни и колеса: 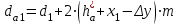 , , 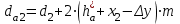 . .Диаметры впадин шестерни и колеса: 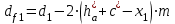 , , 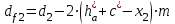 . .Высота зубьев колес: 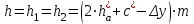 . .Толщины зубьев шестерни и колеса по дугам делительных окружностей: 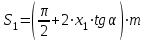 , , 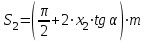 . .Углы профиля зуба в точке на окружности вершин: 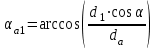 , , 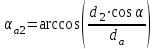 Толщины зубьев по окружности вершин: 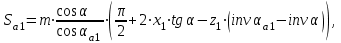 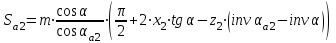 . .Качественные показатели Коэффициент торцового перекрытия: 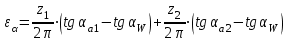 . .Коэффициенты удельного скольжения: 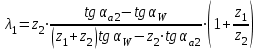 , , 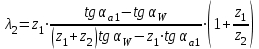 . .Коэффициент удельного давления: 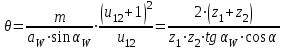 . .Для станочного зацепления Толщина зуба (ширина впадины): 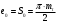 . .Шаг: 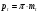 . .Радиус скругления: 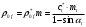 . .Шаг по хорде делительной окружности шестерни: 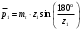 . .Шаг по хорде делительной окружности колеса: 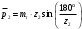 . .3.3 Выбор коэффициентов смещения с учетом качественных показателей. В результате расчета по вышеуказанным формулам на ЭВМ (программа ZUB), получили следующие данные: Таблица 3.3. Задано: Шестерня Колесо Числа зубьев: Z1 = 14 Z2 = 18 Модуль m = 5.0 мм Передача прямозубая Выбрано: Смещение рейки: X1 = 0.60 X2 = 0.50 Результаты расчета: Делительная окружность: R1 = 35.000 мм R2 = 45.000 мм Основная окружность: Rb1 = 32.889 мм Rb2 = 42.286 мм Окружность вершин: Ra1 = 42.141 мм Ra2 = 51.641 мм Окружность впадин: Rf1 = 31.750 мм Rf2 = 41.250 мм Начальная окружность: Rw1 = 37.031 мм Rw2 = 47.611 мм Межцентровое расстояние Aw = 84.641 мм Угол зацепления Alfaw = 27.357 град. Воспринимаемое смещение y = 4.641 мм (0.928) Уравнительное смещение delta y = 0.859 мм (0.172) Высота зуба h = 10.391 мм Толщина зуба: по делительной окружности S1 = 10.038 мм S2 = 9.674 мм по окружности вершин Sa1 = 2.749 мм Sa2 = 3.386 мм Параметры рейки: шаг P = 15.708 мм Угол главного профиля Alfa = 20.0 град. Радиус закругления Ro = 1.900 мм Торцевой зазор с = 1.250 мм Данные для построения графиков качественных характеристик: (см. табл. 1) Данные для построения профилей зубьев (см. табл. 2 и табл. 3) Z1 = 14 Z2 = 18 X1 = 0.600 X2 = 0.500 Координаты середины впадины: ( X,Y ) Шестерня Колесо -7.065 30.954 : -7.163 40.623 Координаты середины вершины зуба: ( X,Y ) 0.000 42.141 : 0.000 51.641 Таблица 1. Данные для построения графиков качественных характеристик: Смещение:Перекрытие:Заострение:Скольжение:Скольжение:Давление: X1 Eps Sa1/m Lam1 Lam2 Teta 0.0 1.33 0.70 7.85 1.24 0.61 0.1 1.30 0.68 5.17 1.26 0.59 0.2 1.28 0.65 3.75 1.27 0.57 0.3 1.25 0.63 2.87 1.29 0.56 0.4 1.22 0.60 2.27 1.30 0.55 0.5 1.19 0.58 1.83 1.31 0.53 0.6 1.16 0.55 1.49 1.32 0.52 0.7 1.13 0.52 1.23 1.33 0.51 0.8 1.10 0.50 1.01 1.34 0.50 0.9 1.07 0.47 0.83 1.36 0.49 1.0 1.04 0.44 0.68 1.37 0.48 1.1 1.01 0.41 0.55 1.38 0.48 1.2 0.98 0.38 0.44 1.39 0.47 Таблицы 2 и 3 Данные для построения профилей зубьев: Z1 = 14 Z2 = 18 X1 = 0.600 X2 = 0.500 Координаты левой боковой поверхности зуба от оси симметрии зуба и центра колеса: Шестерня: X Y X Y :Колесо: X Y X Y 1: -6.780 31.018 -5.172 33.545 : -6.872 43.220 -5.113 43.220 2: -6.660 31.048 -5.110 34.040 : -6.749 43.696 -5.044 43.696 3: -6.542 31.086 -5.024 34.532 : -6.628 44.169 -4.957 44.169 4: -6.427 31.131 -4.916 35.019 : -6.509 44.638 -4.852 44.638 5: -6.314 31.184 -4.790 35.502 : -6.392 45.104 -4.733 45.104 6: -6.205 31.243 -4.647 35.981 : -6.279 45.566 -4.601 45.566 7: -6.100 31.310 -4.489 36.454 : -6.168 46.025 -4.455 46.025 8: -5.998 31.384 -4.316 36.922 : -6.062 46.479 -4.298 46.479 9: -5.901 31.464 -4.129 37.385 : -5.959 46.930 -4.130 46.930 10: -5.809 31.551 -3.931 37.843 : -5.861 47.376 -3.952 47.376 11: -5.722 31.645 -3.720 38.295 : -5.768 47.819 -3.764 47.819 12: -5.640 31.745 -3.498 38.743 : -5.679 48.257 -3.566 48.257 13: -5.564 31.851 -3.265 39.184 : -5.596 48.691 -3.359 48.691 14: -5.494 31.964 -3.022 39.620 : -5.518 49.122 -3.144 49.122 15: -5.430 32.085 -2.769 40.051 : -5.446 49.547 -2.921 49.547 16: -5.373 32.212 -2.507 40.476 : -5.380 49.969 -2.690 49.969 17: -5.322 32.348 -2.236 40.895 : -5.321 50.387 -2.451 50.387 18: -5.279 32.495 -1.957 41.309 : -5.268 50.800 -2.205 50.800 19: -5.244 32.655 -1.670 41.717 : -5.222 51.209 -1.952 51.209 20: -5.218 32.835 -1.374 42.119 : -5.185 51.614 -1.693 51.614 По вычисленным на ЭВМ параметрам построили следующие графики: 1. График изменения коэффициента торцевого перекрытия 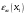 2. Графики изменения коэффициентов скольжения зубьев 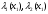 3. График изменения коэффициента удельного давления 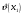 4. График изменения 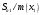 Масштабы построения графиков: 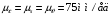 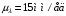 Учитывая, что влияние коэффициента смещения на качественные показатели незначительно, приняли фиксированное значение 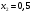 . .При выборе коэффициента смещения учитывали следующие основные рекомендации: 1) проектируемая передача не должна заклинивать; 2) коэффициент перекрытия передачи должен быть больше допустимого 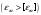 ; ;3) зубья у передачи не должны быть подрезаны, и толщина их на окружности вершин должна быть больше допустимой 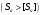 . .Отсутствие подрезания обеспечивается при наименьшем 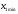 , отсутствие заострения – при максимальном значении коэффициента смещения , отсутствие заострения – при максимальном значении коэффициента смещения 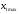 . Значение . Значение 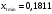 вычисляется на ЭВМ. Для определения значения вычисляется на ЭВМ. Для определения значения 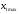 на графике провели линию на графике провели линию 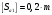 до пересечения с кривой до пересечения с кривой 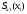 . В точке их пересечения получили значение . В точке их пересечения получили значение 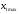 . Таким образом, выделили зону «подрезание-заострение». Затем провели линию . Таким образом, выделили зону «подрезание-заострение». Затем провели линию 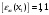 до пересечения с графиком до пересечения с графиком 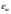 . Таким образом, определили область дозволенных решений по . Таким образом, определили область дозволенных решений по 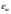 . В этой области по рекомендации ГОСТ 16532-81 выбран коэффициент смещения . В этой области по рекомендации ГОСТ 16532-81 выбран коэффициент смещения 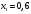 . .Коэффициент перекрытия: 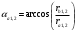 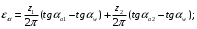 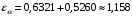 . .С другой стороны коэффициент перекрытия определяется формулой: 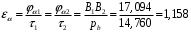 . .Таблица 3.3 Параметр Обозначение Инденти- фикатор Числовое значение Число зубьев шестерни z1 z1 14 Число зубьев колеса z2 z2 18 Модуль m m 5 Радиальный зазор Cm c*m 1,25 Смещение исх. контура x2m x2*m 2,5 Радиусы делительных окружностей r1 r1 35,000 r2 r2 45,000 Радиусы основных окружностей rb1 rb1 32,889 rb2 rb2 42,286 Радиус скругления основания ножки зуба 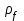 ro 1,9 Шаг торцовый pt pt 15,708 Шаги по хордам p1 p1x 15,576 p2 p2x 15,628 Толщина зуба исх. контура s0 so 7,854 Смещение исх. контура x1m x1*m 3 Воспринимаемое смещение ym y*m 4,641 Уравнительное смещение 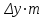 dy*m 0,859 Радиусы начальных окружностей rw1 rw1 37,031 rw2 rw2 47,611 Межосевое расстояние aw aw 84,641 Радиусы окружностей вершин ra1 ra1 42,141 ra2 ra2 51,641 Радиусы окружностей впадин rf1 rf1 31,750 rf2 rf2 41,250 Высота зубьев колеса h h 10,391 Толщина зубьев по делительной окружности s1 s1 10,038 s2 s2 9,674 Угол зацепления передачи 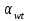 alfwt 27,357 Толщина зубьев по дугам окружностей вершин sa1 sa1 2,749 sa2 sa2 3,386 3.4 Построение профиля зуба колеса, изготовляемого реечным инструментом; построение зубчатой передачи. Масштаб построений 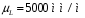 . .Рассмотрим подробнее процедуру построения: 3.4.1 Построение станочного зацепления. Профиль зуба изготовляемого колеса воспроизводиться, как огибающая ряда положений исходного производящего контура реечного инструмента в станочном зацеплении. При этом эвольвентная часть профиля зуба образуется прямолинейной частью исходного производящего контура реечного инструмента, а переходная кривая профиля зуба – закругленным участком. Построения производились следующим образом. Провели делительную rw1 и основную rb1 окружности, окружности вершин ra1 и впадин rf1. Откладывали от делительной окружности с учетом знака смещения x1m и проводили делительную прямую исходного производящего контура реечного инструмента. Эта прямая проходит выше делительной окружности колеса, что соответствует положительному смещению инструмента x1m. На расстоянии ha* m вверх и вниз от делительной прямой провели прямые граничных точек, а на расстоянии (hc*m+C*m) - прямые вершин и впадин; станочно-начальную прямую Q-Q провели касательной к делительной окружности в точке Р0 (полюс станочного зацепления). Провели линию станочного зацепления N0Р0 через полюс станочного зацепления Р0 касательно к основной окружности в точке N0. Эта линия образует с прямыми исходного производящего контура инструмента углы 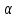 . .Строили исходный производящий контур реечного инструмента так, чтобы ось симметрии впадины совпадала с вертикалью. Симметрично относительно вертикали РО строили профиль второго исходного производящего контура. Расстояние между одноименными профилями зубьев сходного контура равно шагу р= 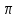 m. m.Построили профиль зуба проектируемого колеса, касающегося профиля исходного производящего контура в точке К. Для построения ряда последовательных положений профиля зуба исходного производящего контура, проводили вспомогательную прямую касательно к окружности вершин М-М. Зафиксировали точку W пересечения линий с прямолинейной частью профиля инструмента, а также положение центра закругленного участка профиля - точку L. Далее отложили на прямой ММ, станочно-начальной прямой QQ и на делительной окружности отрезки равной длины. При перекатывании без скольжения станочно-начальной прямой по делительной окружности, точка W описывает укороченную эвольвенту, а точка L – удлиненную; данные кривые были построены методом треугольников. Из точек L проводят окружности радиусом ρf , а через соответствующие им точки W касательно к этим окружностям – прямые, дающие новое положение исходного производящего контура. К полученному ряду положений профиля зуба исходного профиля провели огибающую, которая определяет левый профиль зуба изготовляемого колеса. Далее производили копирование зубьев по делительной окружности. 3.4.2 Построение проектируемой зубчатой передачи. Откладывали межосевое расстояние аw и проводили окружности rw1 rw2 делительные r1, r2, и основные rb1, rb2, окружности вершин rа1, rа2, и впадин rf1, rf2, Начальные окружности касаются в полюсе зацепления. Расстояние между делительными окружностями по осевой линии равно ym. Расстояние между окружностями вершин одного колеса и окружностями впадин другого, измеренное по оси, равно С*m . Через полюс зацепления касательной к основным окружностям колес проводили линию зацепления. В точке касания N1 и N2 называются предельными точками линии зацепления. Буквами В1 и В2 отмечена активная линия зацепления, точка В1 – точка начала зацепления, точка В2 - точка конца зацепления. Зубья шестерни копировали из построения станочного зацепления, а зубья зубчатого колеса получили графическим построением. Профиль зубчатого колеса 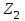 построили как эвольвенту, т.е. траекторию точки М на вспомогательной прямой при обкатывании её по основной окружности радиусом rb2 без скольжения. Переходный профиль принимали приближенно по дуге окружности, радиус которой не менее построили как эвольвенту, т.е. траекторию точки М на вспомогательной прямой при обкатывании её по основной окружности радиусом rb2 без скольжения. Переходный профиль принимали приближенно по дуге окружности, радиус которой не менее 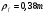 . .3.5 Построение планетарного зубчатого редуктора. В задании задан двухрядный планетарный механизм со смешанным зацеплением. Исходные данные: Число сателлитов в редукторе 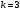 , ,Модуль зубчатых колес взяли равным m=5, Частота вращения электродвигателя из механической характеристики 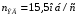 . .Частота вращения вала колеса 5 вычисляется с учетом передаточного отношения колес 5 и 6, по известному значению частоты вращения кривошипа 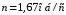 Частота вращения вала колеса z5 – она же – частота вращения водила: 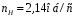 . . |