Брикетировочный автомат - ТММ. 1 Проектирование основного механизма брикетировочного автомата и определение закона движения его начального звена
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
Аналитический метод исследования. Передаточное отношение планетарного редуктора: 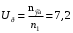 . .Уравнение передаточного отношения: 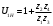 ; ;Уравнение соосности: При равных модулях во всех зацеплениях механизма: 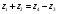 ; ;Условие сборки: 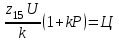 ; ;Условие совместности при 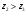 имеет вид: имеет вид: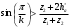 ; ;при 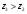 : :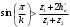 ; ;Решение провели методом сомножителей. Из уравнения передаточного отношения определяют числовое значение 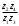 и полученное число раскладывают на сомножители A, B, C и D, которым числа зубьев и полученное число раскладывают на сомножители A, B, C и D, которым числа зубьев 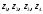 должны быть соответственно пропорциональны. Чтобы обеспечить соосность механизма, ввели дополнительные множители, поставленные в скобки: должны быть соответственно пропорциональны. Чтобы обеспечить соосность механизма, ввели дополнительные множители, поставленные в скобки: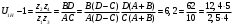 . .С учетом условия соосности для этой схемы 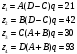 Получаем, что 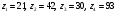 . .Проверим условия существования: Условие отсутствия подрезания 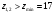 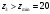 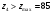 Проверка условия соседства: 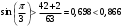 Условие выполняется. Соседство сателлитов обеспечено. Проверка условия сборки: 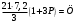 Условие сборки выполняется при P=3. Сборка возможна. Радиусы делительных окружностей колес: 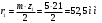 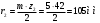 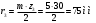 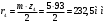 Графический метод исследования. Вычертили схему планетарного механизма в масштабе: 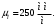 Частота вращения вала 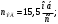 Угловая скорость 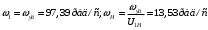 . .Скорость точки А солнечного колеса 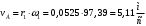 . .Следовательно, масштаб скорости равен: 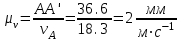 Графически определили передаточное отношение: 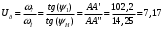 . .Погрешность 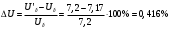 Погрешность определения передаточного отношения укладывается в допустимые рамки (< 4%). 4. Проектирование кулачкового механизма. Дано: график изменения ускорения толкателя, соотношение между ускорениями 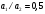 , угол рабочего профиля , угол рабочего профиля 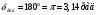 , число оборотов кулачка , число оборотов кулачка 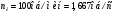 ( (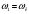 ; ; 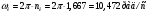 ). Ход толкателя кулачкового механизма ). Ход толкателя кулачкового механизма 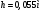 , максимально допустимый угол давления , максимально допустимый угол давления 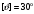 . График ускорений приведен на рисунке 4. . График ускорений приведен на рисунке 4.4.1 Построение кинематических диаграмм методом графического интегрирования. Поскольку исходная функция ускорений толкателя задана в виде графика, то решение получают при помощи графического метода. Для определения передаточной функции скорости толкателя интегрируют заданную функцию ускорения толкателя, затем интегрируют полученную функцию скорости, находя функцию перемещения толкателя. При работе над листом проекта с использованием графического интегрирования все три графика располагают один под другим на одинаковой базе по оси абсцисс. Для заданного случая была выбрана база 180 мм. Тогда масштаб поворота (по оси 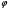 ) вычисляется по формуле: ) вычисляется по формуле: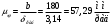 В течение цикла движения толкатель кулачкового механизма должен переместиться из начального положения на величину хода h, а затем возвратиться в исходное положение, т. е. перемещение толкателя на фазе удаления равно перемещению на фазе сближения. Следовательно, график кинематической передаточной функции скорости должен удовлетворять условию равенства площадей под графиком при сближении и удалении толкателя. Скорость и кинематическая передаточная функция скорости толкателя на фазах ближнего и дальнего выстоя равны нулю. Чтобы эти условия выполнялись, необходимо выполнить условия равенства площадей под графиком ускорения в фазах сближения и удаления толкателя. 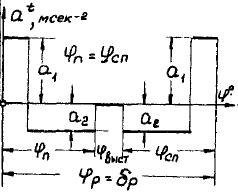 Рис. 4 Рис. 4Для определения вида графика ускорений толкателя, длина участка фазы приближения, имеющая ускорение 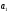 принята за x, а ускорение принята за x, а ускорение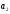 - за y. Тогда, учитывая заданное соотношение - за y. Тогда, учитывая заданное соотношение 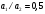 (по условию), и учитывая, что сумма площадей над и под осью абсцисс, должна быть равна нулю: (по условию), и учитывая, что сумма площадей над и под осью абсцисс, должна быть равна нулю: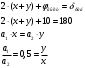 Решая систему из двух уравнений, получили, что 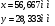 Примем 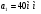 . Тогда . Тогда 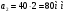 . .График скорости толкателя получили методом графического интегрирования из графика ускорения толкателя. Для этого на продолжении оси 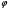 графика ускорений с левой стороны выбран отрезок интегрирования графика ускорений с левой стороны выбран отрезок интегрирования 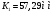 . .После построения графика скорости построен график перемещений толкателя. На продолжении оси абсцисс 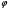 графика скорости также отложен отрезок интегрирования графика скорости также отложен отрезок интегрирования 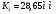 . .Частота вращения кулачка и максимальное перемещение толкателя заданы в исходных данных на проект. Используя их, определили масштабы: Масштаб времени 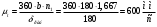 ; ;масштаб перемещений 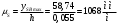 ; ;Здесь 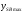 - максимальная ордината на графике перемещения точки B центра ролика толкателя, мм. - максимальная ордината на графике перемещения точки B центра ролика толкателя, мм.масштаб скорости 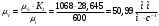 ; ;масштаб ускорений 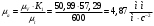 . .Так же, определили масштабы передаточных функций: 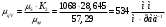 ; ;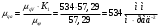 4.2 Определение основных размеров кулачкового механизма. Основные размеры механизма определяются при помощи фазового портрета, представляющего собой зависимость 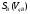 . Для механизма с поступательно перемещающимся толкателем фазовый портрет строят в декартовой системе координат. По оси . Для механизма с поступательно перемещающимся толкателем фазовый портрет строят в декартовой системе координат. По оси 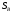 откладывают перемещение толкателя от начала координат в точке откладывают перемещение толкателя от начала координат в точке 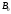 вдоль линии перемещения толкателя. вдоль линии перемещения толкателя.Отрезки, соответствующие перемещениям толкателя, отложены в масштабе графика перемещений 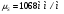 . От полученных точек откладывают отрезки кинематических передаточных функций перпендикулярно линии перемещения толкателя. Масштаб, выбранный по оси . От полученных точек откладывают отрезки кинематических передаточных функций перпендикулярно линии перемещения толкателя. Масштаб, выбранный по оси 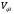 , так же равен масштабу графика перемещений. , так же равен масштабу графика перемещений.Длины отрезков, изображающих кинематические передаточные функции скорости толкателя вычисляют по формуле: 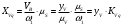 . .Для определения направления вектора передаточной функции скорости следует вектор скорости толкателя повернуть на 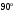 в сторону вращения кулачка (в нашем случае – против часовой стрелки). При этом значение передаточной функции считается положительным при удалении толкателя и отрицательным – при сближении. в сторону вращения кулачка (в нашем случае – против часовой стрелки). При этом значение передаточной функции считается положительным при удалении толкателя и отрицательным – при сближении.Значения 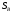 , , 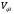 , , 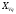 сведены в таблицу 4.2. сведены в таблицу 4.2.Таблица. 4.2
Дополнительно, указали позиции с максимальным значением 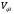 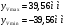 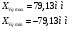 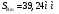 Ограничивая фазовый портрет лучами, ориентированными с учетом [], находим ОДР, внутри которой назначили положение оси О1 (центр вращения кулачка) на пересечении этих лучей. Определили габаритные размеры кулачка 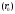 . . 4.3 Построение профиля кулачка. При графическом построении профиля кулачка применили метод обращения движения: всем звеньям механизма условно сообщили угловую скорость, равную 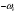 . При этом кулачок становится неподвижным, а остальные звенья вращаются с угловой скоростью, равной по величине, но противоположной по направлению угловой скорости кулачка. . При этом кулачок становится неподвижным, а остальные звенья вращаются с угловой скоростью, равной по величине, но противоположной по направлению угловой скорости кулачка.При построении профиля кулачка с поступательно перемещающимся толкателем, из центра 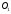 провели окружность радиуса провели окружность радиуса 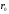 в масштабе в масштабе 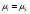 . .Точку пересечения 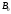 линии перемещения толкателя с окружностью радиуса линии перемещения толкателя с окружностью радиуса 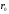 соединили с центром соединили с центром 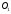 . .От луча 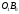 в направлении в направлении 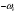 отложили угол рабочего профиля кулачка отложили угол рабочего профиля кулачка 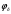 . Дугу, соответствующую углу . Дугу, соответствующую углу 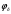 , поделили на части в соответствии с делением оси , поделили на части в соответствии с делением оси 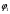 на графике на графике 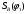 . Получили точки 0,1,2,… На прямых, соединяющих точки 1,2,3,… и . Получили точки 0,1,2,… На прямых, соединяющих точки 1,2,3,… и 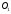 отложили отрезки отложили отрезки 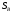 в масштабе в масштабе 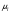 . Получили точки . Получили точки 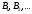 Соединив полученные точки плавной кривой, получили теоретический (центровой) профиль кулачка. Данные занесены в таблицу 4.3. Соединив полученные точки плавной кривой, получили теоретический (центровой) профиль кулачка. Данные занесены в таблицу 4.3.Для получения конструктивного (рабочего) профиля кулачка построили эквидистантный профиль, отстоящий от центрового на величину радиуса ролика. Он получается как огибающая к дугам, проведенным из произвольных точек центрового профиля радиусом ролика: 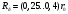 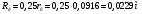 Таблица 4.3
4.4 Построение графика изменения угла давления. Для нахождения углов давления в каждом положении кулачка, провели из точки 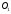 прямые, проходящие через точки 0-12 на графике кинематических отношений, провели вертикальные линии в точках 0-12 и измерили полученные углы. Полученные углы отложили на графике изменения угла давления, выбрав масштаб по оси прямые, проходящие через точки 0-12 на графике кинематических отношений, провели вертикальные линии в точках 0-12 и измерили полученные углы. Полученные углы отложили на графике изменения угла давления, выбрав масштаб по оси 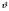 . . Зададимся отрезком 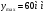 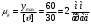 Значения углов приведены в таблице 4.4. Таблица 4.4
Заключение В ходе выполнения курсового проекта были получены следующие результаты: Спроектирована кинематическая схема и определены размеры звеньев механизма: 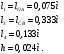 Определен закон движения машинного агрегата, работающего в установившемся режиме. Средняя угловая скорость составляет 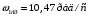 . Движение с необходимым коэффициентом неравномерности вращения . Движение с необходимым коэффициентом неравномерности вращения 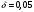 обеспечено установкой дополнительной маховой массы обеспечено установкой дополнительной маховой массы 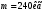 . .Для заданного углового положения механизма 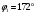 при силе сопротивления, равной при силе сопротивления, равной 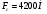 , угловой скорости и ускорением, равными , угловой скорости и ускорением, равными 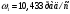 , , 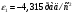 произведен силовой расчет методами кинетостатики. Были определены реакции в кинематических парах механизма, реакции опор и момент движущий: произведен силовой расчет методами кинетостатики. Были определены реакции в кинематических парах механизма, реакции опор и момент движущий: 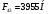 , , 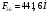 , , 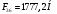 , , 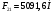 , , 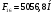 , , 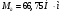 . Относительная погрешность расчета составила . Относительная погрешность расчета составила 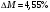 . .Спроектирована прямозубая эвольвентная цилиндрическая зубчатая передача с числами зубьев 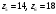 , модулем , модулем 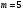 , коэффициентами смещения , коэффициентами смещения 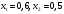 и коэффициентом торцевого перекрытия и коэффициентом торцевого перекрытия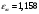 . .Спроектирован двухрядный планетарный редуктор со смешанным зацеплением и с передаточным отношением 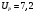 , числами зубьев , числами зубьев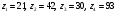 . .Спроектирован центральный кулачковый механизм с поступательно движущимся толкателем. Минимальный радиус теоретического профиля кулачка составил 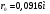 , радиус ролика , радиус ролика 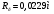 при допустимом угле давления при допустимом угле давления 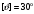 . .Список использованной литературы. Теория механизмов и механика машин. Под редакцией К. В. М.: Издательство МГТУ им. Н.Э. Баумана, 2002г. Учебное пособие для курсового проектирования по теории механизмов и машин. Часть 1. Под редакцией Г.А. Тимофеева. М: Издательство МГТУ им. Н.Э. Баумана, 2000г. Силовой расчет механизмов: учебное пособие. Под редакцией В.Б. Тарабарина. М: Издательство МГТУ им. Н.Э. Баумана, 2000г. Проектирование зубчатых передач и планетарных механизмов с использованием ЭВМ: учебное пособие для курсового проектирования. Под редакцией Г.А. Тимофеева. М.: Типография МВТУ, 1987г. Проектирование кулачковых механизмов. Г.А. Тимофеев, М.В. Самойлова. М.: Издательство МГТУ им. Н.Э. Баумана ,1998г. Конспект лекций по предмету «Теория механизмов и машин». Лектор ‑ Ю.В. Костиков, 2008г. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

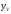 , мм
, мм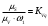 , постоянная
, постоянная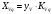 , мм
, мм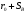 , мм
, мм