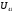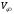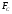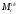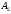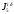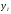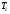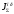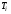Брикетировочный автомат - ТММ. 1 Проектирование основного механизма брикетировочного автомата и определение закона движения его начального звена
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
1 Проектирование основного механизма брикетировочного автомата и определение закона движения его начального звена Расчет производится с целью определения основных размеров кулисного механизма. Используется метод моделирования системы одномассовой модели. В качестве звена приведения принимается кривошип 1. 1.1 Проектирование кинематической схемы и определение длин звеньев механизма Исходные данные модели для расчета размеров механизма (рис 1а.): ход ползуна (5) H, 0,25м.; коэффициент изменения его средней скорости при прямом и обратном ходах KV =1,65; расстояние между осями вращения кривошипа 1 и кулисы 3 a=lOC=0,20м.; кривошип вращается равномерно относительно стойки 6 со скоростью  =const; =const;камень кулисы 2 движется поступательно относительно кулисы 3. 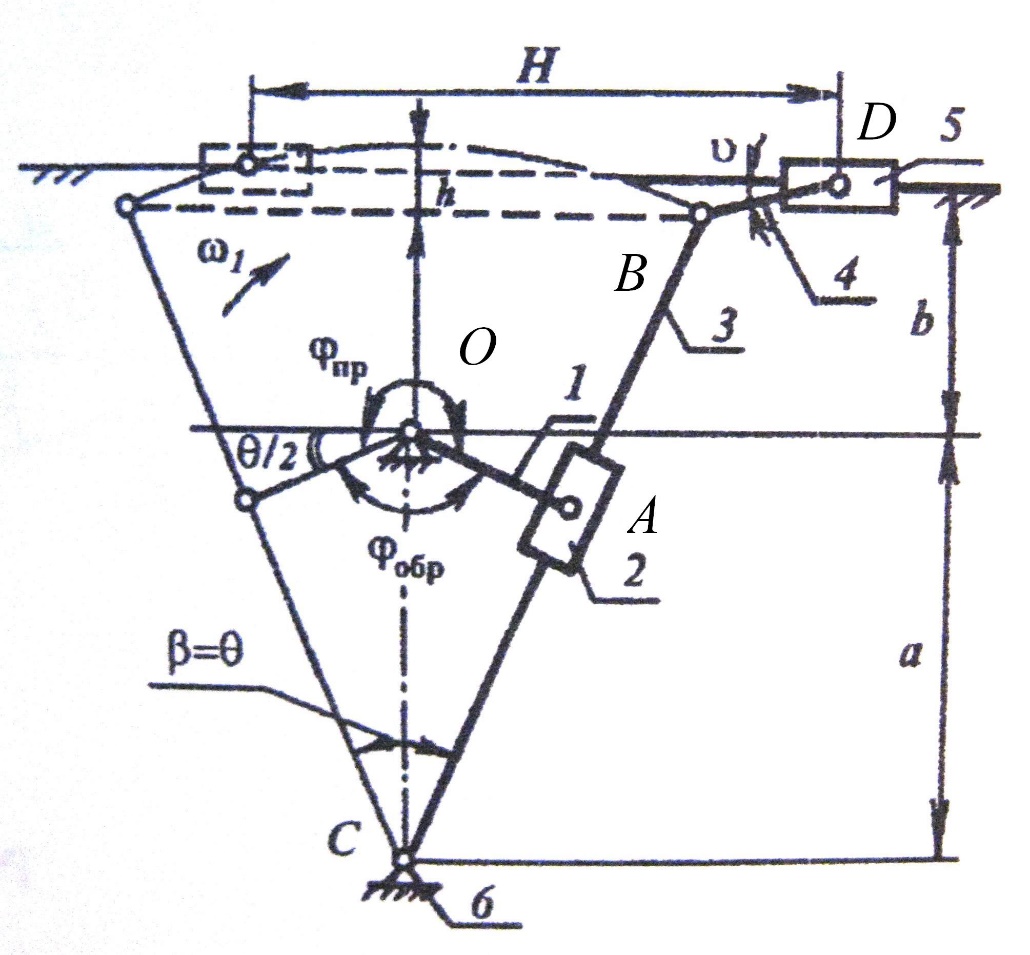 Из уравнения 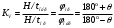 найден угловой ход кулисы (в градусах): найден угловой ход кулисы (в градусах):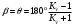 . .Длина кулисы 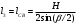 , ,Длина кривошипа 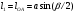 . .При определении размера bследует ориентироваться на минимальные значения угла давления  . Для этого необходимо траекторию точки D расположить так, чтобы она делила пополам стрелку h, длина которой определяется по формуле . Для этого необходимо траекторию точки D расположить так, чтобы она делила пополам стрелку h, длина которой определяется по формуле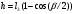 . .Длина 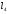 выбрана, согласно условию выбрана, согласно условию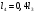 . .Выполнив соответствующие расчеты, получили: 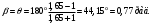 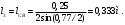 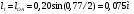 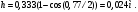 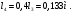 1.2 Расчет кинематических передаточных функций скоростей Кинематические передаточные функции (аналоги скоростей) высчитываются по формулам 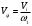 ; ; 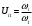 ; ;Для расчета передаточных функций скоростей построили планы возможных скоростей для 12 положений механизма. Используя их, нашли передаточные функции механизма, приведенные к звену 1 для каждого из положений. Результаты занесены в таблицу 1.2. Таблица 1.2
1.3 Построение диаграммы суммарного приведенного момента Для упрощения определения закона движения механизма, реальный механизм заменили одномассовой динамической моделью, и нашли приложенный к ее звену суммарный приведенный момент 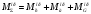 . .Где 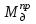 – приведенный движущий момент; – приведенный движущий момент;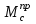 – приведенный момент сил сопротивления; – приведенный момент сил сопротивления;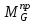 – приведенный момент сил тяжести. – приведенный момент сил тяжести.Приведенный момент 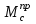 , заменяющий силу сопротивления , заменяющий силу сопротивления 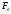 , определен в каждом положении механизма по формуле , определен в каждом положении механизма по формуле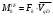 . .Сила 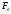 определяется из индикаторной диаграммы усилий прессования. определяется из индикаторной диаграммы усилий прессования.Приведенным суммарным моментом 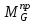 от сил тяжести от сил тяжести 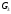 и и 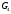 звеньев 3 и 4 пренебреженно, так как он мал по сравнению с звеньев 3 и 4 пренебреженно, так как он мал по сравнению с 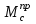 (отличаются в 50-100 раз). (отличаются в 50-100 раз).Таким образом, формула для суммарного приведенного момента имеет вид: 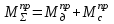 . .Значения 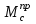 в зависимости от положения начального звена приведены в таблице 1.3. в зависимости от положения начального звена приведены в таблице 1.3.Приведенный момент движущих сил 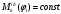 определен из условия, что при установившемся движении определен из условия, что при установившемся движении 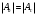 за цикл; за цикл; 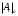 пропорциональна алгебраической сумме площадей пропорциональна алгебраической сумме площадей 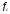 (в квадратных миллиметрах) под кривой (в квадратных миллиметрах) под кривой 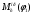 . Тогда: . Тогда: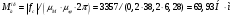 График суммарного приведенного момента 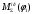 построили путем сложения с учетом знака ординат графиков построили путем сложения с учетом знака ординат графиков 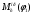 и и 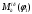 . Значения графика суммарного приведенного момента приведены в таблице 1.3. . Значения графика суммарного приведенного момента приведены в таблице 1.3.Таблица 1.3
1.4 Построение графика суммарной работы всех сил Суммарная работа 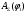 всех сил равна работе всех сил равна работе 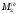 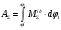 График 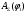 построен методом графического интегрирования графика построен методом графического интегрирования графика 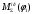 , выбран отрезок интегрирования , выбран отрезок интегрирования 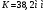 . В конце цикла установившегося движения значение суммарной работы должно быть равно нулю. Масштаб графика . В конце цикла установившегося движения значение суммарной работы должно быть равно нулю. Масштаб графика 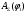 по оси ординат по оси ординат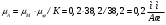 Результаты интегрирования приведены в таблице 1.4. Таблица 1.4
1.5 Построение диаграмм приведенных моментов инерции звеньев Исходные данные: Таблица 1.5.1
Приведенный момент инерции 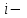 го звена механизма найден из условия равенства кинетических энергий всех звеньев механизма и звена приведения, т.е. из закона сохранения кинетической энергии. го звена механизма найден из условия равенства кинетических энергий всех звеньев механизма и звена приведения, т.е. из закона сохранения кинетической энергии.Для звена движущегося поступательно 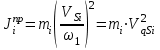 При вращательном движении i-го звена вокруг неподвижной оси k: 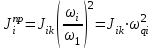 , ,если на вращающемся i-м звене задан момент инерции 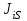 относительно оси, проходящей через центр масс Si, а последний не совпадает с осью вращения k, то относительно оси, проходящей через центр масс Si, а последний не совпадает с осью вращения k, то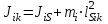 . .При плоскопараллельном движении 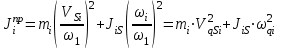 График приведенных моментов инерции 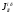 второй группы звеньев построили по выше приведенным формулам, используя полученные ранее значения передаточных функций (см. таблицу 1.2). второй группы звеньев построили по выше приведенным формулам, используя полученные ранее значения передаточных функций (см. таблицу 1.2).В механизме брикетировочного аппарата во II группу звеньев входят звено 3 – кулиса, звено 4 и звено 5 – ползун. Приведенные моменты инерции этих звеньев находятся по формулам: 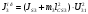 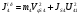 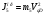 Построили соответствующие графики, а так же график суммы этих функций - 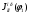 . .Значения приведенных моментов инерции звеньев, а так же их сумма приведены в таблице 1.5.2. Таблица 1.5.2
1.6 Построение диаграмм кинетической энергии механизма График полной кинематической энергии всего механизма 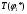 получили по зависимости получили по зависимости 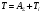 . .График кинетической энергии 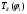 (приближенный) второй группы звеньев получили, выполнив переход от построенного графика (приближенный) второй группы звеньев получили, выполнив переход от построенного графика 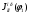 , пересчитав масштаб по формуле: , пересчитав масштаб по формуле: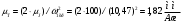 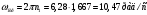 График кинетической энергии 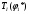 I группы звеньев (приближенный) построили по уравнению I группы звеньев (приближенный) построили по уравнению 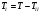 . .В каждом положении механизма из ординат кривой 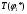 вычли ординаты вычли ординаты 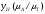 , равные значениям , равные значениям 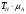 в соответствующих положениях механизма. Ординаты в соответствующих положениях механизма. Ординаты 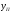 взяли с графика взяли с графика 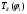 : :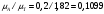 Полученные значения занесены в таблицу 1.6 Таблица 1.6
1.7 Определение необходимого момента инерции маховых масс и выбор размеров и массы маховика Необходимый момент инерции маховых масс 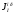 , учитывая коэффициент неравномерности, определили по формуле (допущение, что , учитывая коэффициент неравномерности, определили по формуле (допущение, что 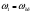 при построении графика при построении графика 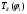 , не вносит существенной ошибки в расчет при нашем значении , не вносит существенной ошибки в расчет при нашем значении 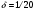 ) ) 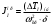 . .Максимальное изменение кинетической энергии первой группы звеньев за период цикла нашли следующим образом: 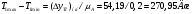 Тогда 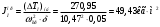 Момент инерции первой группы звеньев пересчитали, приведя его к выходному валу редуктора. Для этого определим передаточное отношение угловых скоростей главного вала и выходного вала редуктора (из условия – вал кривошипа расположен на том же валу, что и зубчатое колесо 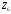 ): ):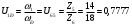 Момент инерции нашли по формуле: 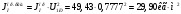 Момент инерции дополнительной маховой массы 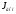 (маховика) определяем по формуле (момент инерции вращающихся деталей, приведенный к выходному звену редуктора, берется из условия): (маховика) определяем по формуле (момент инерции вращающихся деталей, приведенный к выходному звену редуктора, берется из условия):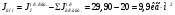 Маховик выбран в виде сплошного диска (рис. 1.7). В осевом сечении он имеет форму прямоугольника с наружным диаметром D и толщиной b. 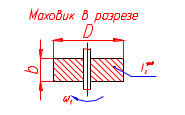 рис. 1.7 рис. 1.7Размеры маховика определяем по расчетным формулам: Диаметр 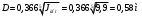 Ширина 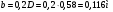 Масса 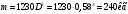 1.8 Определение закона движения механизма Чтобы найти угловую скорость начального звена, необходимо знать начальные условия, которые для установившегося режима движения заранее неизвестны. Поэтому воспользуемся тем, что при малых значениях коэффициента неравномерности верхняя часть графика, изображающая изменение кинетической энергии, приближенно изображает также изменение угловой скорости. График (приближенный) угловой скорости 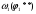 получили, осуществив переход от графика получили, осуществив переход от графика 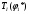 , то есть, определили масштаб угловой скорости по формуле: , то есть, определили масштаб угловой скорости по формуле: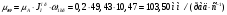 Расстояние от линии 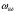 до оси абсцисс нашли по формуле: до оси абсцисс нашли по формуле: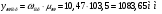 По графику нашли значение 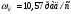 После этого нашли кинетическую энергию механизма в начальном положении: 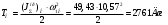 Также найдем значения угловой скорости начального звена в каждом положении цикла. 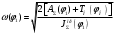 Результаты представлены в таблице 1.8 Таблица 1.8
|