Ответ на билет. 1. Расчет основных параметров цикла идеального и реального компрессора
 Скачать 59.54 Kb.
|
|
1. Расчет основных параметров цикла идеального и реального компрессора. Принципиальная схема и цикл одноступенчатого одноцилиндрового горизонтального компрессора представлен на рис. 1. При движении поршня 2 слева направо давление газа в цилиндре становится меньше давления во всасывающем патрубке. Всасывающий клапан (клапаны обозначены цифрой 3) открывается и по мере движения поршня вправо полость цилиндра заполняется газом теоретически по линии 4-1. При обратном движении поршня справа налево всасывающий клапан закрывается и поршень сжимает газ теоретически по кривой 1-2, пока давление в цилиндре не достигнет давления Р2, равного давлению газа в нагнетательной линии трубопровода. Открывается нагнетательный клапан и поршень выталкивает газ в нагнетательную линию трубопровода при постоянном давлении Р2 (линия 2-3). В начале нового хода поршня слева направо вновь открывается всасывающий клапан, давление в цилиндре падает с Р2 до Р1 теоретически мгновенно (линия 3-4) и процесс повторяется.  Рис. 1 Принципиальная схема и идеальный цикл компрессора простого действия При рассмотрении идеального цикла поршневого компрессора принимают следующие допущения: 1. Отсутствуют сопротивления движению потока газа (в том числе и в клапанах). 2. Давление и температура газа во всасывающей и нагнетательной линиях постоянны. 3. Давление и температура газа в период всасывания, так же как и в период выталкивания газа из цилиндра, не меняются. 4. Мертвое (вредное) пространство в цилиндре компрессора отсутствует. 5. Нет потерь мощности на трение и нет утечек газа. При изотермическом процессе газ сжимается по кривой 1-2"', при адиабатическом 1-2", а при политропическом 1-2 или 1-2'. Рассматривая политропический процесс 1-2, видим, что за этот период цикла объем газа уменьшится с V1 до V2, давление изменится от р1 до р2, а температура - от Т1 до Т2. При нагнетании газа в трубопровод (2-3) давление и температура газа остаются неизменными (р2 и Т2). Весь объем газа V2 переходит в нагнетательный трубопровод. За период 3-4 в цилиндре снижается давление до давления во всасывающем трубопроводе (р1). Период всасывания (4-1) характеризуется постоянным давлением Р1 и температурой газа Т1, в цилиндр поступает объем газа, равный V1. Работа сжатия газа от давления всасывания р1 до давления нагнетания р2 в цилиндре компрессора за время одного цикла характеризуется площадью индикаторной диаграммы, ограниченной линиями, которые соединяют точки 1-2-3-4. В случае идеального процесса, когда исключены все непроизводительные потери энергии, затрачиваемая энергия равна полезной. Таким образом, индикаторная диаграмма в этом случае дает величину затрачиваемой и полезной работы. При изотермическом процессе газ сжимается без нагрева и выходит с меньшей температурой, чем при адиабатическом или политропическом процессах. Поскольку компрессор предназначен только для сжатия и перемещения газа, то повышение его температуры не является полезной для нас частью работы. Поэтому изотермический процесс (без нагрева газа) более выгоден. При этом процессе на сжатие газа от давления р1 до давления р2 затрачивается меньше энергии (рис. 1, площадь 1-2"'-3-4 наименьшая). Однако изотермический процесс трудно осуществить на практике, и компрессоры работают при политропическом или адиабатическом процессе. В реальном компрессоре в силу сопротивления нагнетательного клапана и трубопровода давление р2* (точка m на рис.2) в конце сжатия и при нагнетании выше давления р2 среды, куда происходит нагнетания. Поэтому нагнетание изобразится линией 2-m-3. Выступ m в начале нагнетания обусловлен инерцией нагнетательного клапана. От точки 3 рабочее тело, оставшееся во вредном пространстве, расширяется - линия 3-4 (рис.2), и реальная индикаторная диаграмма компрессора замыкается. 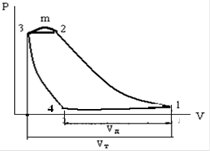 Рис. 2 Реальная индикаторная диаграмма поршневого компрессора При поступлении в цилиндр рабочее тело получает тепло от стенок цилиндра, так как температура его при всасывании ниже температуры стенок. Кроме того, оно получает тепло от смешения с газом или паром, оставшимся во вредном пространстве от предыдущего цикла работы и расширившимся до давления всасывания р1*. В результате температура рабочего тела t1* оказывается больше температуры тело получает тепло от стенок цилиндра, так как температура его при всасывании ниже температуры стенок. Кроме того, оно получает тепло от смешения с газом или паром, оставшимся во вредном пространстве от предыдущего цикла работы и расширившимся до давления всасывания р1*. В результате температура рабочего тела t1* оказывается больше температуры - среды t1, из которой происходит всасывание. Поэтому объем рабочего тела, действительно всасываемого в цилиндр за один ход поршня, т.е. всасываемый - объем при параметрах р1* и t1*, изображается на индикаторной диаграмме отрезком Vд. Рабочий объем цилиндра - объем между крайними положениями поршня - обозначен Vт. 2. Полное термическое сопротивление при теплопередаче от одной жидкости к другой. Плотность теплового потока, обусловленная теплопроводностью через твердую стенку, определяется уравнением Фурье:  Тот же тепловой поток передается от поверхности стенки к жидкости за счет теплоотдачи, и описывается уравнением Ньютона-Рихмана:  Пусть плоская и однородная стенка имеет толщину δ. На одной поверхности стенки заданы граничные условия первого рода в виде t=tc1 (при x=0); на другой поверхности заданы коэффициент теплоотдачи α2 и температура окружающей среды tж2, т. е. граничные условия третьего рода. Внутренние источники в стенке отсутствуют (qv=0).  Задача сводится к нахождению плотности теплового потока от горячей стенки к холодной жидкости q,и температуры на поверхности стенки tс2. Систему уравнений можно записать в виде: Отсюда плотность теплового потока 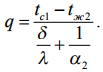 Обозначим:  Величина k называется коэффициентом теплопередачи и измеряется в Вт/(м2К). Она характеризует интенсивность передачи теплоты. Линейный коэффициент численно равен количеству теплоты, которое проходит через стенку площадью 1 м 2 в единицу времени от одной среды к другой при разности температур между ними 1 К. Величина R, (м 2 К)/Вт, называется полным термическим сопротивлением. Она равна:  Полное термическое сопротивление складывается из частных термических сопротивлений, причем 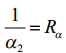 термическое сопротивление теплопроводности стенки;  термическое сопротивление теплопередачи от поверхности стенки к жидкости. |