Давление идеального газа на твердую стенку

• Название: Давление идеального газа на твердую стенку
• Дата: 13.04.2022
• Размер: 358.88 Kb.
• Имя файла: Termodinamika_i_molekulyarnaya_fizika_9-16.docx
• Тип: Документы; #470708

УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА

Давление идеального газа на твердую стенку

Идеальным будем называть газ, молекулы которого не взаимодействуют между собой, исключая лишь кратковременный процесс столкновений, во время которого происходит взаимный обмен энергией и импульсом.

Будем степень разреженности идеального газа характеризовать объемной концентрацией его молекул n=N/Vn=N/V.

 

За счет взаимных столкновений между молекулами устанавливается равновесное распределение по скоростям (распределение Максвелла), которое характеризуется определенной температурой TT, одинаковой для всего объема газа и стенок сосуда.

Рассчитаем давление PP идеального газа на стенку сосуда как средний импульс, передаваемый молекулами единице площади стенки в единицу времени:

P=F¯¯¯¯S=1S(dpdt)¯¯¯¯¯¯¯¯¯¯¯¯¯¯.

Давление – есть плотность потока импульса на стенку.

Направим ось координат OxOx перпендикулярно стенке. Импульс, передаваемый одной молекулой, имеющей при подлете компоненту скорости vxvx, стенке при упругом отскоке¹ по скоростям надо проводить в пределах от минус до плюс бесконечности. При одинаковой температуре газа и стенки (при этих условиях испаренные молекулы имеют такое же распределение по скоростям, что и падающие на нее) результат расчета будет такой же, как и для упругого отскока.}, равен 2mvx2mvx. Обоснование этой величины показано на рис.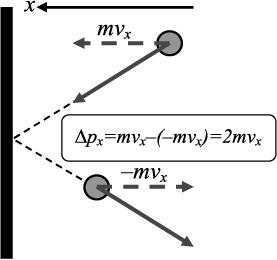

 

Количество молекул с данным значением проекции скорости vxvx, падающих в единицу времени на единицу площади (поток частиц), равно



где нормированная на единицу функция распределения φ(vx)φ(vx) дается первой формулой (15.15). Тогда для среднего потока импульса (16.1) (это и есть давление) получим искомую величину:

(16.2)

Здесь средний поток импульса по времени заменен на средний поток по ансамблю падающих молекул, а интегрирование при усреднении по ансамблю проводится от 0 до ∞∞, так как давление на стенку создается только молекулами, летящими к ней. Мы также воспользовались определением среднего значения кинетической энергии молекул (15.14) и равновероятностью трех его компонент.

Уравнение (16.2) называют основным уравнением кинетической теории идеального газа.

Из (16.2) видно, что для данного количества молекул газа NN произведение PVPV зависит только от средней кинетической энергии молекул, которая, как утверждает МКТ, определяется только абсолютной температурой TT.

Другое следствие (16.2), известное как закон Дальтона, гласит: если идеальный газ является смесью различных молекул, то полное давление является суммой парциальных давлений, оказываемых на стенку каждой компонентой смеси независимо от присутствия других компонент:

(16.3)

Замечательно то, что давление газа зависит только от концентрации молекул и температуры, но не от массы и сорта молекул. Это значит, что при одинаковой температуре и давлении в единице объема содержится равное число молекул любого газа. Это утверждение известно как закон Авогадро. Он первоначально был установлен экспериментально, но не получил сразу какого-либо теоретического объяснения.

 Уравнение состояния идеального газа

Число молекул NN в объеме VV можно всегда представить как произведение числа молей вещества на число молекул в одном моле NANA: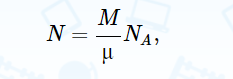



где MM – масса газа, μμ – масса одного моля газа (молярная масса), NA=6.02⋅1023NA=6.02⋅1023 – постоянная Авогадро.

Молем вещества называют такое его количество, которое содержит 

В результате из (16.2) получаем известное уравнение Клапейрона−Менделеева, которое связывает только макроскопические параметры: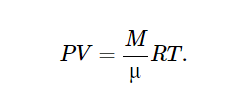

(16.4)

(16.4)

Здесь введена новая постоянная величина R=kNA=8.31R=kNA=8.31 Дж/(моль⋅⋅К) – газовая постоянная.

Фактически уравнение (16.4) определяет абсолютную температуру, и оно может быть получено из общих рассуждений исходя из смысла температуры. Но здесь, следуя традиции, мы начали рассмотрение термодинамики из статистической гипотезы и пока не определили само понятие термодинамической температуры. Это будет сделано в следующем параграфе.

Уравнение (16.4) называется уравнением состояния идеального газа. Его можно записать и в «микроскопическом виде»: P=nkT, который легче запоминается. Посмотрим на некоторые следствия (16.4).

Барометрическая формула

Применим уравнение состояния (16.4) для расчета равновесной зависимости давления газа от высоты в однородном поле тяготения.

Для этого выделим в столбе газа прямой цилиндр с единичной площадью основания и достаточно маленькой высотой dhdh, как показано на рис. 16.2.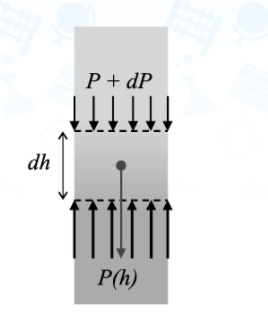



Так как выделенный объем газа находится в покое, то действующая на него суммарная сила должна быть равна нулю. Это значит, что разность давлений на двух высотах должна быть равна весу газа (на рисунке вес обозначен центральной стрелкой), находящегося между этими высотами:



Из уравнения состояния (16.4) найдем: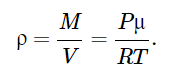



Подставим это выражение в равенство (16.5) и проинтегрируем его: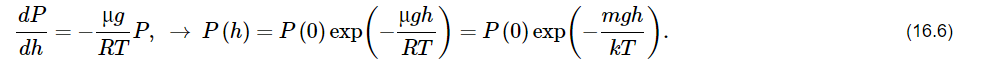



Это и есть знаменитая барометрическая формула. Здесь P(0)P(0) – давление газа на начальной высоте h=0h=0, а m=μ/NAm=μ/NA – масса одной молекулы.

Если эту зависимость переписать для концентрации частиц, то она останется верной для любых микрочастиц (например, пыли или капельного аэрозоля):



Формулу (16.7) можно применить и к смеси газов, каковой является и воздух. Поскольку молекулы идеальных газов не взаимодействуют друг с другом, каждый газ можно рассматривать отдельно, то есть формула (18.7) применима к парциальному давлению каждой компоненты смеси. Чем больше масса молекулы газа, тем быстрее его давление убывает с высотой. Именно по этой причине наблюдается некоторое относительное обеднение воздуха кислородом и аргоном по сравнению с азотом на больших высотах.

Следует иметь в виду, что применимость формулы (16.7) к реальной атмосфере весьма ограничена. Она верна только для равновесной изотермической атмосферы, что не имеет места в действительности (температура атмосферы заметно меняется с высотой над уровнем моря). Кроме того, формула выведена в предположении, что величина gg не меняется с высотой.

Именно формула (16.7) послужила основой для определения постоянной Авогадро в опытах французского физика Перрена, за что ученый был удостоен Нобелевской премии по физике. Сложность эксперимента состояла в том, чтобы добиться максимально возможного равенства размеров всех капелек в эмульсии. Схема опыта Перрена показана на рисунке 16.3.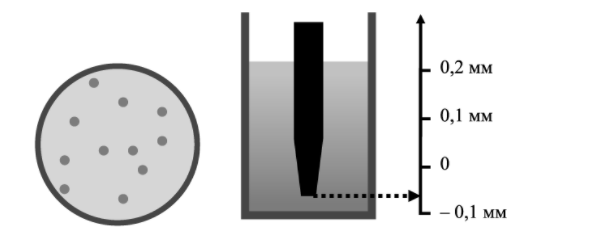



Перрен с помощью микроскопа очень точно измерял концентрацию маленьких капелек гуммигута (это краска, образующая мелкодисперсную эмульсию в воде), взвешенных в воде, в зависимости от высоты. Измеряя n(h)n(h), Перрен из зависимости (16.7) с высокой точностью определил постоянную Больцмана kk. Зная точно измеренную к тому времени газовую постоянную RR, удалось определить также постоянную Авогадро.

Внутренняя энергия газа

Исследуем теперь процесс перехода механической энергии, расходуемой на сжатие или расширение идеального газа, во внутреннюю энергию его молекул.

Легко показать (см. рисунок 16.4), что при расширении объема, занимаемого газом, на малую величину dVdV, последний совершает работу δA∼F dxδA∼F dx над внешними телами или окружающей средой:



Здесь интегрирование давления идет по всей поверхности SS того объема, который занят газом, а dV=S dxdV=S dx. Если dV<0dV<0, то есть газ сжимается, то работа становится отрицательной. Это означает, что внешние силы совершают работу над газом.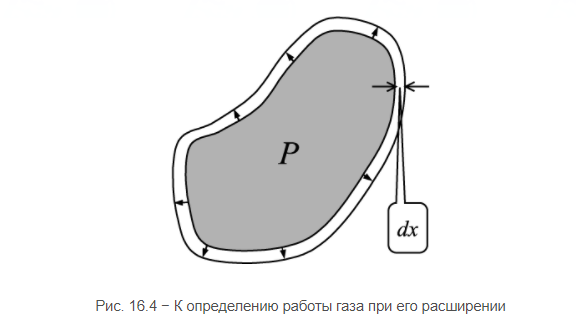



Газ может совершать работу только за счет расходования своей внутренней энергии и возможного притока тепловой энергии δQδQ в него из внешней среды.

Это утверждение, выражающее закон сохранения энергии, называется первым началом термодинамики:



Отметим, что в формулах (16.8) и (16.9) малые изменения работы и количества теплоты отмечены не так, как изменение внутренней энергии. Это сделано для того, чтобы различать случай изменения величины, зависящей только от параметров начального и конечного состояний системы (например, dUdU – изменение внутренней энергии), и изменения величины, зависящей не только от параметров начального и конечного состояния, но и от параметров перехода из одного состояния в другое (δAδA и δQδQ – производство работы и сообщение тепловой энергии в некотором процессе).

Очевидно, что внутренняя энергия UU данной массы MM идеального одноатомного газа – это суммарная кинетическая энергия молекул, которая полностью определяется его температурой, как это следует из (15.6):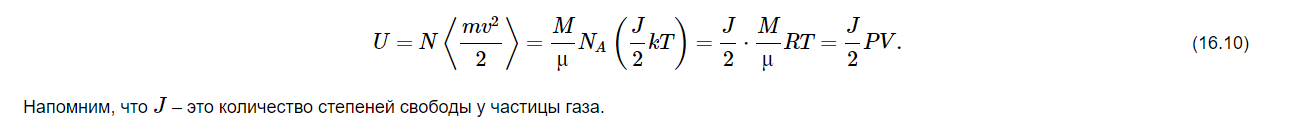

Адиабатический процесс

Если какая-либо система меняет свои макроскопические параметры без теплообмена с внешними телами, то такой процесс называется адиабатическим.

Найдем связь объема с давлением при адиабатическом процессе изменения параметров идеального газа из (16.9):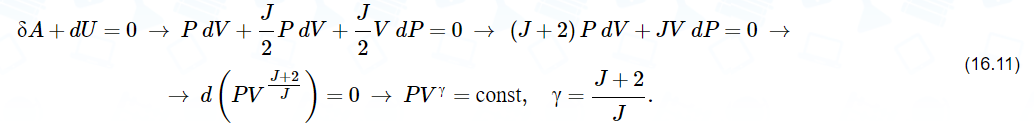



Показатель степени γγ, называемый показателем адиабаты, зависит от структуры молекул газа (от строения молекулы зависит число степеней свободы JJ). Так как показатель адиабаты непосредственно может быть измерен экспериментально, то в термодинамике газа принято именно его считать заданным, а внутреннюю энергию и количество степеней свободы выражать через него:



Из (16.11) видно, что при адиабатическом сжатии газа его давление растет быстрее, чем при изотермическом сжатии, так как в процессе адиабатического сжатия растет температура газа. Это механическая работа перешла во внутреннюю энергию: совершая над газом работу, мы увеличиваем среднюю кинетическую энергию молекул, которая прямо пропорциональна абсолютной температуре.

Газовые законы

Поскольку состояние данной массы газа характеризуется тремя параметрами, связанными уравнением состояния (16.4), то можно один из параметров фиксировать, а два других при этом будут связаны однозначной зависимостью.

Изотермический процесс происходит при постоянной температуре. Давление и объем подчиняются закону Бойля-Мариотта:

PV=const

Изобарический (изобарный) процесс происходит при поcтоянном давлении, а объем и температура подчиняются закону Гей-Люссака:

V=const⋅T

Изохорический (изохорный) процесс происходит при постоянном объеме, а давление и температура подчиняются закону Шарля:

P=const⋅T

В отличие от вышеназванных равновесный адиабатический процесс протекает тоже при сохранении определенной физической величины – энтропии. Эта величина исключительно теоретическая (ее нельзя непосредственно измерить каким-либо прибором), она была введена в термодинамику по аналогии с остальными изопараметрическими процессами, где что-то остается неизменным¹.

Теплоемкость идеального газа

Введем понятие теплоемкости системы.

Теплоемкостью физического тела, и газа в частности, будем называть величину, равную количеству подводимой к телу тепловой энергии, необходимой для изменения его температуры на один Кельвин:



где значок αα обозначает определенные условия подвода тепла. В теории вещества удобно использовать молярную теплоемкость – теплоемкость одного моля вещества¹.

Теплоемкость – это характеристика не только вещества, но и процесса подвода тепла.

Если, например, подвод тепла осуществляется при постоянном объеме идеального газа, то вся тепловая энергия идет на увеличение его внутренней энергии. Для одного моля газа из (16.12) и уравнения состояния PV=RT имеем:



Если же процесс подвода тепла происходит при постоянном давлении (в соответствии с законом Гей-Люссака газ при этом должен расширяться), то часть тепловой энергии пойдет на совершение работы δAδA, а не только на увеличение внутренней энергии. Вот почему теплоемкость изобарического процесса должна быть больше: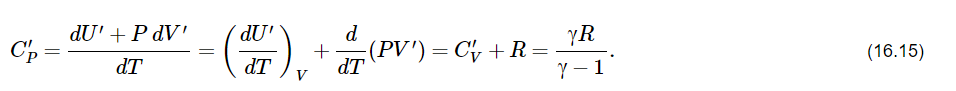



вязь между двумя теплоемкостями идеального газа CP=CV+RCP=CV+R называют иногда уравнением Майера. Из (16.14) и (16.15) видно, что эту же связь можно записать через показатель адиабаты:



Эта связь дает один из способов определения показателя адиабаты: надо просто измерить теплоемкость газа в различных условиях нагревания: при фиксированном объеме газа и фиксированном давлении.

Молярные величины будем отмечать штрихом, например C′.

Равновесные состояния и равновесные процессы

Будем называть термодинамической системой любое макроскопическое тело, находящееся в равновесном или близком к равновесному состоянии.

Состояния любой системы могут быть заданы с помощью ряда параметров. Так, для газа или жидкости это – давление PP, объем VV и температура TT.

Не в любом состоянии все ее параметры имеют определенный смысл. Например, при заполнении газом сосуда в первые моменты времени давление и температура газа различны в разных точках объема. Аналогично, при расширении газа в вакуум нельзя с определенностью говорить об объеме, занимаемом газом. Опыт показывает, что такие состояния не остаются неизменными, если они не поддерживаются искусственно. По прошествии некоторого времени устанавливается состояние, в котором каждый параметр имеет одно и то же значение в каждой точке системы и остается неизменным сколь угодно долго, если не меняются внешние условия. Такие состояния называются равновесными. Если равновесие не установилось и в системе существуют градиенты макроскопических параметров, то состояние называется неравновесным.

Процесс перехода системы из неравновесного состояния в равновесное называется процессом релаксации.

При этом для выравнивания значения каждого параметра по всему объему системы существует свое характерное время – время релаксации.

Можно представить себе процесс, протекающий в системе со скоростью, значительно меньшей скорости релаксации. Это значит, что на любом этапе такого процесса значения всех макроскопических параметров в различных частях системы будут успевать выравниваться и этот процесс будет представлять собой последовательность бесконечно близких друг к другу равновесных состояний. Такие достаточно медленные процессы принято называть равновесными или квазистатическими.

Ясно, что все реальные процессы являются неравновесными и могут лишь приближенно считаться равновесными. В равновесном процессе в любой момент времени градиенты всех параметров равны нулю.

Отсюда следует, что в силу симметрии процесс может идти как в прямом, так и в противоположном направлениях. Поэтому равновесный процесс может быть обращен во времени, и при обратном изменении внешних условий система пройдет те же состояния, что и при прямом процессе, но в обратной последовательности. В связи с этим равновесные процессы называют также обратимыми. Равновесные (обратимые) процессы можно изображать графически на плоскости параметров.

Изотермический процесс

Изменение энтропии, а также количество произведенной работы и подведенной теплоты в изотермическом процессе из (18.1) найти нетрудно: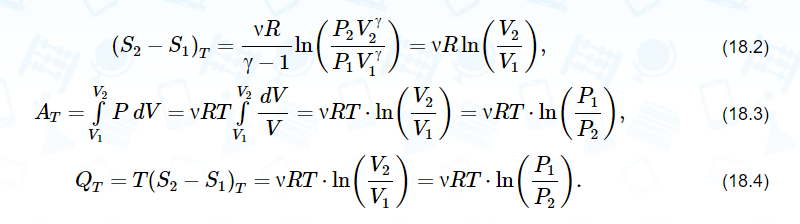



Идеальный газ в изотермическом процессе совершает работу исключительно за счет подвода тепловой энергии (AT=QT). Это происходит потому, что внутренняя энергия идеального газа не зависит от объема, и в изотермическом процессе не изменяется. Графики изотермического процесса показаны на рис. 18.1.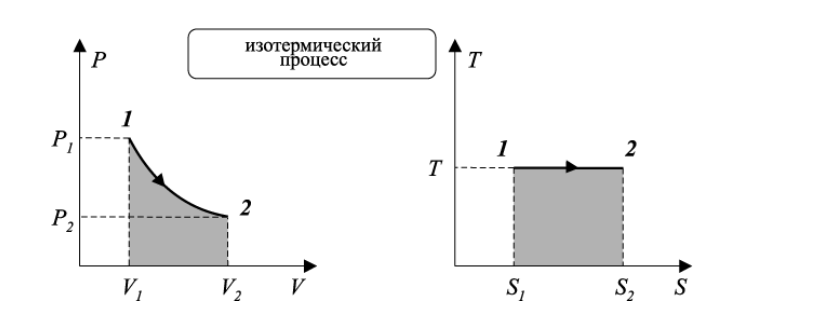