Ответы на вопросы ТУР. 1. Реакторные измерения. 2 2 Нейтронные источники. 4

• Название: 1. Реакторные измерения. 2 2 Нейтронные источники. 4
• Анкор: Ответы на вопросы ТУР.docx
• Дата: 13.12.2017
• Размер: 6.93 Mb.
• Имя файла: Ответы на вопросы ТУР.docx
• Тип: Документы; #11333
• страница: 27 из 39

51 Процедура ступенчатого пуска и ядерная безопасность.

Переходные процессы n(t) в подкритическом реакторе при шаговом подъёме поглотителей шагами одинаковой величины в процессе пуска ЯР

Осторожность и правила ядерной безопасности диктуют следующие меры.

а) Количество тепловыделяющих сборок в активной зоне реактора должно быть заранее рассчитано.

Загрузка их в реактор осуществляется порциями не более чем по ¼ от полного расчетного количества.

б) Критическое положение подвижных поглотителей заранее должно быть рассчитано.

Оператор заранее должен отчётливо представлять, до какой высоты ему предстоит поднимать поглотители от нижних концевых выключателей.

Без проверенного и утверждённого компетентными ответственными лицами расчёта пускового критического положения органов СУЗ пуск реактора не разрешается.

в) Последовательность и темп подъёма групп поглотителей задаётся специальной программой безопасного подъёма их при пуске.

Суть этой программы состоит в том, что подъём поглотителей в критическое положение выполняется осторожными шагами, каждый из которых уменьшает величину степени подкритичности реактора не более чем на 0.3 b_э.

Между шагами должны выдерживаться временные паузы, большие по величине, чем время стабилизации подкритической плотности нейтронов в реальных условиях пуска.

Ясно, что в начальной стадии подъёма поглотителей, когда реактор глубоко подкритичен, изменения плотности нейтронов с каждым шагом поглотителей вверх относительно малы. Поэтому нет никакого смысла делать значительные паузы между шагами.

Система линейных дифференциальных уравнений, описывающая временное поведение плотности нейтронов в «точечном» приближении при изменении реактивности в реакторе с учетом запаздывающих нейтронов в отсутствие внешнего источника :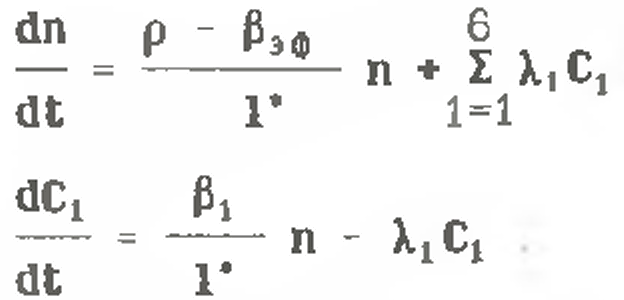



Всего имеется 7 дифференциальных уравнений. Первое уравнение характеризует изменение плотности нейтронов во времени. Остальные 6 уравнений описывают изменение концентрации ядер-предшественников i-й группы во времени.

Общие решения :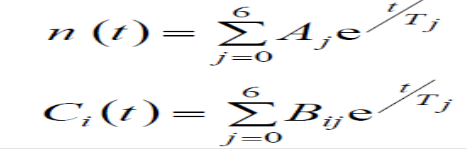



Шесть слагаемых в решениях имеют экспоненциальные множители с отрицательными периодами (то есть эти слагаемые затухают) и одно слагаемое, содержащее экспоненциальный множитель с периодом, модуль которого больше модуля любого из отрицательных периодов, а знак совпадает со знаком реактивности.

Именно это слагаемое определяет асимптотическое развитие нестационарного процесса, а соответствующий период называется асимптотическим.

По истечении времени, необходимого для завершения переходного процесса формирования установившегося спектра эмиттеров запаздывающих нейтронов, плотность нейтронов и концентрации эмиттеров всех групп изменяются по одинаковому экспоненциальному закону с общим асимптотическим периодом.

При ступенчатом изменении реактивности решение системы имеет вид:



Показатель экспоненты ω₀ имеет тот же знак, что и возмущение ρ а показатели остальных шести экспонент (ω₁, ω₂. . . ω₆) отрицательны при любом значении ρ.

Коэффициенты А₀. А₁, . .,А₆ определяются начальными условиями. А₀ положителен при любом знаке ρ, а коэффициенты А₁, А₂….А₆ имеют знак, обратный знаку возмущения ρ. Причем сумма всех A_i равна 1

Из анализа уравнения следует, что все экспоненты, кроме экспоненты с ω₀, через очень малый промежуток времени затухают, и в дальнейшем изменение плотности нейтронов в реакторе будет определяться только первым слагаемым:

n(t) = n₀  A₀ exρ(ω₀t)

Величина Т_у = Т₀ = 1/ω₀ называется поэтому установившимся периодом реактора. Иногда значения Т₁= 1/ωi, Т₂= 1/ω₂,…Т₆=l/ω₆ называют переходными периодами реактора.

Существует характеристическое уравнение системы, связывающее реактивность с установившимся периодом реактора (уравнение Нордхейма). которое иногда называют «формулой обратных часов» :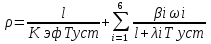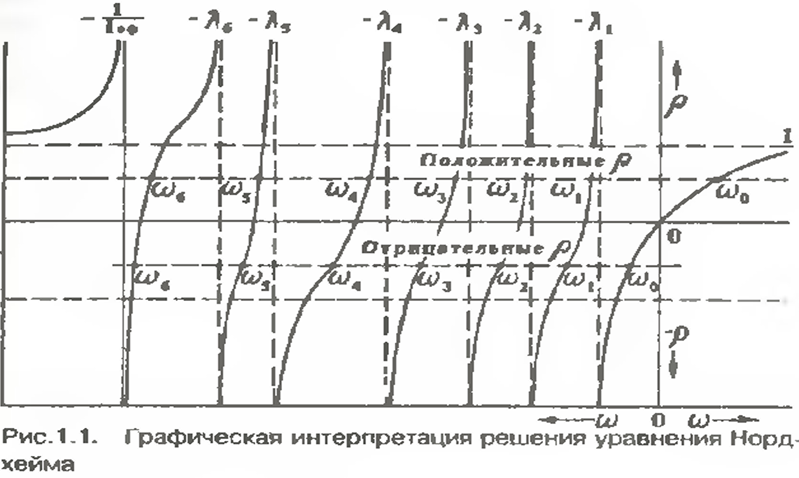





Графическое представление решения уравнения Нордхейма для шести групп запаздывающих нейтронов. Из графиков наглядно видно, что каждому значению ρ соответствует семь значений w_i (i = 0, 1,…6). С увеличением ρ корни уравнения асимптотически приближаются к значениям -λ₁ , -λ₂. .. . -λ₆.

Область, выделенная горизонтальными пунктирными линиями, ограничена значениями ρ=±1. Для расчета кинетики реакторов практически важная область находится при |ρ| << 1.

Уравнение Нордхейма имеет большое практическое значение, так как позволяет вычислить реактивность по измеренному установившемуся периоду и наоборот - по заданной реактивности определить установившийся период реактора. При малых значениях ρ<<β_зф установившийся период велик и в знаменателе под знаком суммы в уравнении можно пренебречь единицей по сравнению с произведением λ_iТ_у. при достаточно малом ρ эффективный коэффициент размножения близок к единице, и можно записать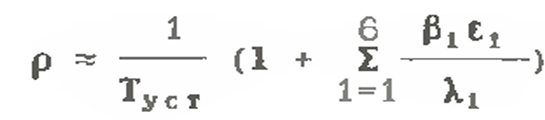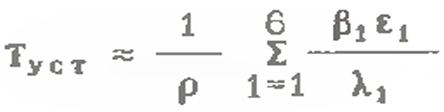





Отсюда следует, что установившийся период при малых значениях ρ не зависит от времени жизни мгновенных нейтронов и скорость переходного процесса определяется только свойствами запаздывающих нейтронов.

При больших значениях ρ время жизни мгновенных нейтронов начинает оказывать влияние на величину установившегося периода Т_у. Для крайнего случая, когда ρ>>β_эф установившийся период будет настолько мал, что в произведением λ_iT_y по сравнению с единицей можно пренебречь и ρ