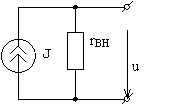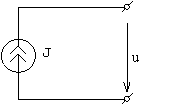шпоры по электротехнике. ШПОРЫ по электре. 1 Реальные и идеальные источники эл энергии. Схемы замещения
 Скачать 1.36 Mb.
|
|
1 Реальные и идеальные источники эл. энергии. Схемы замещения. Любой источник электрической энергии преобразует другие виды энергии (механическую, световую, химическую и др.) в электрическую. Ток в источнике электрической энергии направлен от отрицательного вывода к положительному за счет сторонних сил, обусловленных видом энергии, которую источник преобразует в электрическую. Реальный источник электрической энергии при анализе электрических цепей можно представить либо в виде источника напряжения, либо в виде источника тока. Ниже это показано на примере обыкновенной батарейки.
Способы представления реального источника электрической энергии отличаются друг от друга схемами замещения (расчетными схемами). На рис. 15 реальный источник представлен (замещен) схемой источника напряжения, а на рис. 16 реальный источник представлен (замещен) схемой источника тока.
Период (T) - время (с), в течение которого переменная величина совершает полное колебание. Частота - число периодов в секунду. Единица измерения частоты - Герц (сокращенно Гц), 1 Гц равен одному колебанию в секунду. Период и частота связаны зависимостью T = 1 / f. Изменяясь с течением времени, синусоидальная величина (напряжение, ток, ЭДС) принимает различные значения. Значение величины в данный момент времени называют мгновенным. Амплитуда - наибольшее значение синусоидальной величины. Амплитуды тока, напряжения и ЭДС обозначают прописными буквами с индексом: Im, Um, Em, а их мгновенные значения - строчными буквами i, u, e. Мгновенное значение синусоидальной величины, например тока, определяют по формуле i = Imsin(ωt + ψ), где ωt + ψ — фаза-угол, определяющий значение синусоидальной величины в данный момент времени; ψ - начальная фаза, т. е. угол, определяющий значение величины в начальный момент времени. Синусоидальные величины, имеющие одинаковую частоту, но разные начальные фазы, называются сдвинутыми по фазе. 3 На рис. 2 приведены графики синусоидальных величин (тока, напряжения), сдвинутых по фазе. Когда же начальные фазы двух величин равны ψi = ψu, то разница ψi − ψu = 0 и, значит, сдвига фаз нет φ = 0 (рис. 3). Эффективность механического и теплового действия переменного тока оценивается действующим его значением. Действующее значение переменного тока равно такому значению постоянного тока, который за время, равное одному периоду переменного тока, выделит в том же сопротивлении такое же количество тепла, что и переменный ток. Действующее значение обозначают прописными буквами без индекса: I, U, E. Рис. 2 Графики синусоидальных тока и напряжения, сдвинутых по фазе. Рис. 3 Графики синусоидальных тока и напряжения, совпадающих по фазе 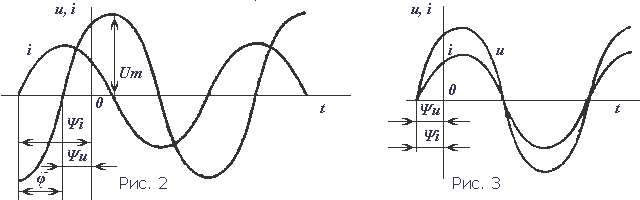 Для синусоидальных величин действующие и амплитудные значения связаны соотношениями: I=IM/√2; U=UM/√2; E=EM√2. Действующие значения тока и напряжения измеряют амперметрами и вольтметрами переменного тока, а среднее значение мощности - ваттметрами. 4.Действующим (эффективным) значениемсилыпеременного тока называют величину постоянного тока, действие которого произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток за время одного периода. В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение силы переменного тока. Иначе говоря, действующее значение тока можно определить по формуле: 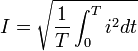 .Для гармонических колебаний тока  5Формула индуктивного сопротивления:  где L — индуктивность. Формула емкостного сопротивления: где С — емкость. Предлагаем рассмотреть цепь переменного тока, в которую включено одно активное сопротивление, и нарисовать ее в тетрадях. После проверки рисунка рассказываю, что в электрической цепи (рис. 1, а) под действием переменного напряжения протекает переменный ток, изменение которого зависит от изменения напряжения. Если напряжение увеличивается, ток в цепи возрастает, а при напряжении, равном нулю, ток в цепи отсутствует. Изменение направления его также будет совпадать с изменением направления напряжения (рис. 1, в). 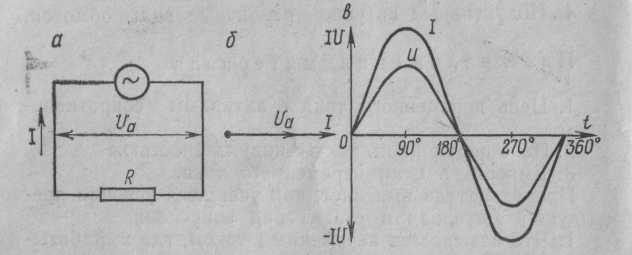 Рис 1. Цепь переменного тока с активным сопротивлением: а – схема; б – векторная диаграмма; в – волновая диаграмма Графически изображаю на доске синусоиды тока и напряжения, которые совпадают по фазе, объясняя, что хотя по синусоиде можно определить период и частоту колебаний, а также максимальное и действующее значения, тем не менее построить синусоиду довольно сложно. Более простым способом изображения величин тока и напряжения является векторный. Для этого вектора напряжения (в масштабе) следует отложить вправо из произвольно выбранной точки. Вектор тока преподаватель предлагает учащимся отложить самостоятельно, напомнив, что напряжение и ток совпадают по фазе. После построения векторной диаграммы (рис. 1, б) следует показать, что угол между векторами напряжения и тока равен нулю, т. е. ? = 0. Сила тока в такой цепи будет определяться по закону Ома: Вопрос 2. Цепь переменного тока с индуктивным сопротивлением Рассмотрим электрическую цепь переменного тока (рис. 2, а), в которую включено индуктивное сопротивление. Таким сопротивлением является катушка с небольшим количеством витков провода большого сечения, в которой активное сопротивление принято считать равным 0. 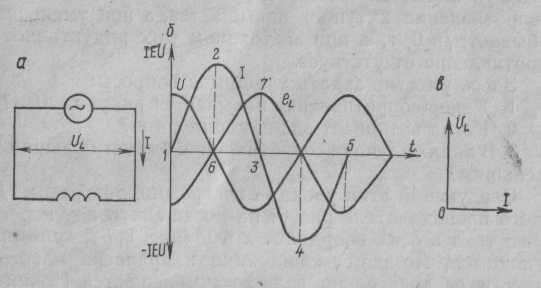 Рис. 2. Цепь переменного тока с индуктивным сопротивлением Вокруг витков катушки при прохождении тока и будет создаваться переменное магнитное поле, индуктирующее в витках эдс самоиндукции. Согласно правилу Ленца, эде индукции всегда противодействует причине, вызывающей ее. А так как эде самоиндукции вызвана изменениями пе-ременного тока, то она и препятствует его прохождению. Сопротивление, вызываемое эде самоиндукции, называется индуктивным и обозначается буквой xL. Индуктивное со-противление катушки зависит от скорости изменения то-ка в катушке и ее индуктивности L: где ХL– индуктивное сопротивление, Ом;  – угловая частота переменного тока, рад/с; L–индуктивность ка-тушки, Г.Угловая частота ==  , следовательно,  .Емкостное сопротивление в цепи переменного тока. Перед началом объяснения следует напомнить, что имеется ряд случаев, когда в электрических цепях, кроме активного и индуктивного сопротивлений, имеется и емкостное сопротивление. Прибор, предназначенный для накопления электрических зарядов, называется конденсатором. Простейший конденсатор – это два проводка, разделенных слоем изоляции. Поэтому многожильные провода, кабели, обмотки электродвигателей и т. д. имеют емкостное сопротивление. Объяснение сопровождается показом конденсатора различных типов и емкостных сопротивлений с подключением их в электрическую цепь. Предлагаю рассмотреть случай, когда в электрической цепи преобладает одно емкостное сопротивление, а активным и индуктивным можно пренебречь из-за их малых значений (рис. 6, а). Если конденсатор включить в цепь постоянного тока, то ток по цепи проходить не будет, так как между пластинами конденсатора находится диэлектрик. Если же емкостное сопротивление подключить к цепи переменного тока, то по цепи будет проходить ток /, вызванный перезарядкой конденсатора. Перезарядка происходит потому, что переменное напряжение меняет свое направление, и, следовательно, если мы подключим амперметр в эту цепь, то он будет показывать ток зарядки и разрядки конденсатора. Через конденсатор ток и в этом случае не проходит. Сила тока, проходящего в цепи с емкостным сопротивлением, зависит от емкостного сопротивления конденсатора Хс и определяется по закону Ома  где U – напряжение источника эдс, В; Хс – емкостное сопротивление, Ом; / – сила тока, А. 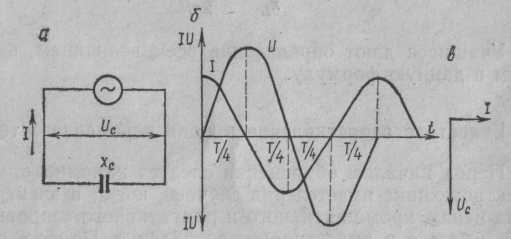 Рис. 3. Цепь переменного тока с емкостным сопротивлением Емкостное сопротивление в свою очередь определяется по формуле  где С – емкостное сопротивление конденсатора, Ф. Предлагаю учащимся построить векторную диаграмму тока и напряжения в цепи с емкостным сопротивлением. Напоминаю, что при изучении процессов в электрической цепи с емкостным сопротивлением было установлено, что ток опережает напряжение на угол ф = 90°. Этот сдвиг фаз тока и напряжения следует показать на волновой диаграмме. Графически изображаю на доске синусоиду напряжения (рис. 3, б) и дает задание учащимся самостоятельно нанести на чертеж синусоиду тока, опережающую напряжение на угол 90° 6 Последовательное соединение R, L, С 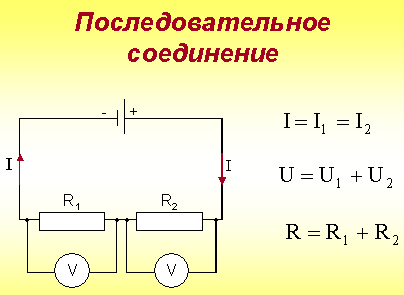 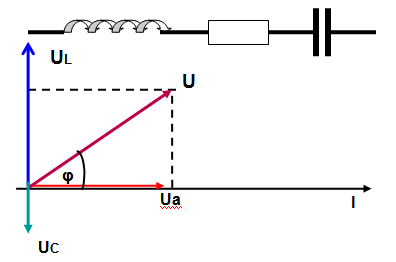 При прохождении гармонического тока i = Imcosωt через электрическую цепь, состоящую из последовательно соединенных элементов R, L, С (рисунок 2.13), на зажимах этой цепи создается гармоническое напряжение, равное алгебраической сумме гармонических напряжений на отдельных элементах (второй закон Кирхгофа): и = uR + иL + uC. (2.14)  Напряжение uR на сопротивлении R совпадает по фазе с током i, напряжение uL на индуктивности L опережает, а напряжение иC на емкости С отстает от i на π/2 (рисунок 2.14).  7 Резонанс в последовательном контуре. Резонанс частоты. Волновое сопротивление. Добротность. Последовательным колебательным контуром называется цепь, составленная из последовательно соединенных индуктивности, ёмкости и активного сопротивления, характеризующего потери в реактивных элементах контура (рис.2.1.).  Рис.2.1 При воздействии гармонической ЭДС  ток в контуре,  где   Активную составляющую входного сопротивления R можно приближенно считать не зависящей от частоты генератора. Реактивная составляющая  является функцией частоты и в зависимости от величины L, C, и изменяется по величине и знаку (рис2.2.). 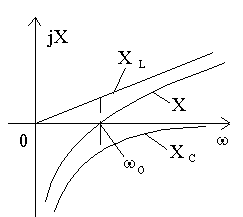 Рис.2.2 Режим цепи, при котором XL=-XC(X=0), называется резонансом напряжений. При резонансе 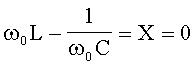 , откуда где 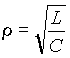 - величина, имеющая размерность сопротивления и называемая волновым или характеристическим сопротивлением контура. Следовательно, при резонансе- напряжение на резисторе равно напряжению на входе контура; - напряжения на реактивных элементах одинаковы и пропорциональны волновому сопротивлению контура; - соотношение напряжения на входе контура (на резисторе) и напряжений на реактивных элементах определяется соотношением резистивного и волнового сопротивлений. Отношение волнового сопротивления к резистивному /R = Q, называется добротностью контура, а величина обратная D=1/Q - затуханием. Таким образом, добротность числено равна отношению напряжения на реактивном элементе контура к напряжению на резисторе или на входе в режиме резонанса. Добротность может составлять несколько десятков единиц и во столько же раз на-пряжение на реактивных элементах контура будет превышать входное 8   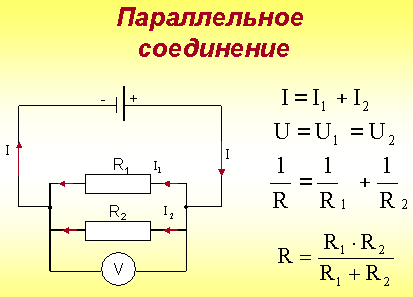 При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников. Режим резонанса можно создать также при параллельном соединении R, L и C (рис. 8а)). Такая цепь называется параллельным резонансным контуром. В этом случае условие резонанса удобнее сформулировать для мнимой части комплексной проводимости в виде Следовательно, для параллельного контура возможны те же вариации параметров, что и для последовательного и выражения для них будут идентичными.  При изменении частоты питания изменяется только мни-мая составляющая вектора комплексной проводимости Y , поэтому его конец перемещается на комплексной плоскости по прямой параллельной мнимой оси и проходящей че-рез точку G=1/R , соответствующую вещественной составляющей проводимости (рис. 8 б)). При частоте резонанса модуль вектора минимален, а при стремлении частоты к нулю и бесконечности, его значение стремится к бесконечности. При этом угол сдвига фаз между током и напряжением на входе контура стремится к 90 при 0 и к 90 при . Для параллельного соединения токи в отдельных элементах можно представить через проводимости и общее падение напряжения U в виде  Пусть в режиме резонанса падение напряжения на входе контура равно U0, тогда токи в отдельных элементах будут  где  - волновая или характеристическая проводимость контура. Как следует из выражений (17), при резонансе токи в реактивных элементах одинаковы, а входной ток равен току в резисторе R. Отношение Q= /G называется добротностью, а величина обратная D=1/Q - затуханием параллельного резонансного кон-тура. Таким образом, добротность равна отношению токов в реактивных элементах контура к току на входе или в резисторе. В электрических цепях добротность может достигать значений в несколько десятков единиц и во столько же раз токи в индуктивности и емкости будут превышать входной ток. Поэтому резонанс в параллельном контуре называется резонансом токов. Электрической проводимостью называется способность материала пропускать через себя электрический ток.  Как видно, полное сопротивление является геометрической суммой активного и реактивного сопротивлений. Сопротивление, оказываемое проводником проходящему на нему переменному току, называется активным сопротивлением. При прохождении переменного тока через них необходимо учитывать не только активное, но и реактивное сопротивление, обусловленное наличием, в потребителе индуктивных и емкостных свойств его. 9Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.  где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 - I2 + I3 - I4 + I5 = 0  Рис. 1 В этом уравнении токи, направленные к узлу, приняты положительными. Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре  где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.  Рис. 2 Так, для замкнутого контура схемы (рис. 2) Е1 - Е2 + Е3 = I1R1 - I2R2 + I3R3 - I4R4 Замечание о знаках полученного уравнения: 1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура; 2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода. 10.Методика расчета цепи методом контурных токов  В методе контурных токов за неизвестные величины при-нимаются расчетные (контурные) токи, которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи. Расчет токов ветвей по методу контурных токов выполняют в следующем порядке: 1 Вычерчиваем принципиальную схему цепи и обозначаем все элементы. 2 Определяем все независимые контуры. 3 Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры (I11, I22, I33 и т. д.) или римские цифры. 4 По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности. 5 Решаем любым методом полученную систему относительно контурных токов и определяем их. 6 Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.). 7 Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу. 11 Метод узловых напряжений состоит в определении напряжений между узлами сложной электрической цепи путем решения уравнений, составленных по первому закону Кирхгофа, куда в качестве неизвестных входят напряжения между узлами цепи. Рассмотрим применение метода для простейшей цепи с двумя узлами (рис.3), в которой к двум узлам "х" и "y" подключены "n" ветвей.  Пусть величины ЭДС, сопротивления резисторов ветвей заданы. Необходимо найти все токи схемы. По этому методу сначала определяют напряжение Uхy между узлами "х" и "y" схемы, а затем находят токи всех ветвей. Предположим, что Uхy известно и направлено от узла "x" к узлу "y". Выберем произвольно положительные направления токов ветвей. Причем, в пассивных ветвях токи должны быть направлены от узла с более высоким потенциалом (в на-шем случае это узел "х") к узлу с низким потенциалом, в активных ветвях направления токов выбираются произвольно. Применяя к каждой из ветвей закон Ома для активного участка цепи, выразим их токи:  где - …… - проводимости соответствующей ветви схемы. По первому закону Кирхгофа для токов ветвей, сходящихся в узле "х", можно записать: Подставляем вместо токов их значения из системы.  Из этого равенства определяется напряжение :  или  Напряжение между узлами параллельной цепи равно алгебраической сумме произведений проводимости и ЭДС каждой ветви, деленной на сумму проводимостей всех ветвей схемы. Произведение GкЕк берут со знаком "+" в том случае, когда направление ЭДС Ек противоположно выбранному условно-положительному направлению Uхy, и со знаком "-", когда эти направления совпадают. Зная напряжение Uхy, пользуясь системой уравнений, можно определить токи ветвей схемы. 12  Трехфазная цепь является совокупностью трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе на 120o, создаваемые общим источником. Участок трехфазной системы, по которому протекает одинаковый ток, называется фазой. Трехфазная цепь со-стоит из трехфазного генератора, соединительных про-водов и приемников или нагрузки, которые могут быть однофазными или трехфазными. Трехфазный генератор представляет собой синхронную машину. На статоре гене-ратора размещена обмотка, состоящая из трех частей или фаз, пространственно смещенных относительно друг друга на 120o. В фазах генератора индуктируется симметричная трехфазная система ЭДС, в которой электродвижущие силы одинаковы по амплитуде и различаются по фазе на 120o. Запишем мгновенные значения и комплексы действующих значений ЭДС.  Соответственно На схемах трехфазных цепей начала фаз обозначают первыми буквами латинского алфавита (А, В, С), а концы - последними буквами (X, Y, Z). Направления ЭДС указывают от конца фазы обмотки генератора к ее началу. Каждая фаза нагрузки соединяется с фазой генератора двумя проводами: прямым и обратным. Получается не-связанная трехфазная система, в которой имеется шесть соединительных проводов. Чтобы уменьшить количество соединительных проводов, используют трехфазные цепи, соединенные звездой или треугольником. 7.2. Соединение в звезду. Схема, определения Цепь трехфазного переменного тока состоит из трехфазного источника питания, трехфазного потребителя и проводников линии связи между ними. Симметричный трехфазный источник питания можно представить в виде трех однофазных источников, работающих на одной частоте с одинаковым напряжением и имеющих временной угол сдвига фаз 120˚. Эти источники могут соединяться звездой или треугольником. При соединении звездой условные начала фаз используют для подключения трех линейных проводников A, B, C, а концы фаз объединяют в одну точку, называемую ней-тральной точкой источника питания (трехфазного генератора или трансформатора). К этой точке может подключаться нейтральный провод N. Схема соединения фаз источника питания звездой приведена на рисунке 1, а.  Рис. 1. Схемы соединения фаз источника питания: а – звездой; б – треугольником. Напряжение между линейным и нейтральным проводами называется фазным, а между линейными проводами – линейным. В комплексной форме записи выражения для фазных напряжений имеют вид:  Соответствующие им линейные напряжения при соединении звездой:  Здесь Uф – модуль фазного напряжения источника питания, а Uл – модуль линейного напряжения. В симметричной трёхфазной системе, при соединении фаз источника звездой, между этими напряжениями есть взаимосвязь:  При включении фаз треугольником фазные источники пи-тания соединяют последовательно в замкнутый контур (рисунок 1, б). Из точек объединения источников между собой выводятся три линейных провода A, B, C, идущие к нагрузке. Из рисунка 1, б видно, что выводы фазных источников подключены к линейным проводникам, а следовательно, при соединении фаз источника треугольником фазные напряжения равны линейным. Нейтральный провод в этом случае отсутствует. К трехфазному источнику может подключаться нагрузка. По величине и характеру трёхфазная нагрузка бывает симметричной и несимметричной. В случае симметричной нагрузки комплексные сопротивления всех трёх фаз одинаковы, а если эти сопротивления различны, то нагрузка несимметричная. Фазы нагрузки мо-гут соединяться между собой звездой или треугольником (рисунок 2), независимо от схемы соединения источника.  Рис. 2. Схемы соединения фаз нагрузки 7.3. Соединение в треугольник. Схема, определения. Если конец каждой фазы обмотки генератора соединить с началом следующей фазы, образуется соединение в треугольник. К точкам соединений обмоток подключают три линейных провода, ведущие к нагрузке. На рис. 7.3 изображена трехфазная цепь, соединенная треугольником. Как видно из рис. 7.3, в трехфазной цепи, соединенной треугольником, фазные и линейные на-пряжения одинаковы.Uл = Uф IA, IB, IC - линейные токи; Iab, Ibc, Ica- фазные токи. Линейные и фазные токи нагрузки связаны между собой первым законом Кирхгофа для узлов а, b, с.   Рис. 7.3 Линейный ток равен геометрической разности соответствующих фазных токов. На рис. 7.4 изображена векторная диаграмма трехфазной цепи, соединенной треугольником при симметричной нагрузке. Нагрузка является симметричной, если со-противления фаз одинаковы. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений, так как нагрузка состоит из активных сопротивлений.  Рис. 7.4 Из векторной диаграммы видно, что  ,Iл= √3 Iф при симметричной нагрузке. Трехфазные цепи, соединенные звездой, получили большее распространение, чем трехфазные цепи, соединенные треугольником. Это объясняется тем, что, во-первых, в цепи, соединенной звездой, можно получить два напряжения: линейное и фазное. Во-вторых, если фазы обмотки электрической машины, соединенной треугольником, находятся в неодинаковых условиях, в обмотке появляются дополнительные токи, нагружающие ее. Такие токи отсутствуют в фазах электрической машины, соединенных по схеме "звезда". Поэтому на практике избегают соединять обмотки трехфазных электрических машин в треугольник. | |||||||||||||||||||||||||||||||||||||||||||||||
