Матан зачёт. 1 семестр Вопросы к зачету
 Скачать 282 Kb. Скачать 282 Kb.
|
|
Приложение 1 к рабочей программе 7.3.1. Примерные вопросы для самостоятельной подготовки к зачету/экзамену 1 семестр Вопросы к зачету Матрицы. Основные понятия и определения. Операции сложения, умножения на скаляр, матричное умножение. Матрицей называют прямоугольную таблицу, заполненную числами. Важнейшие характеристики матрицы – число строк и число столбцов. Если у матрицы одинаковое число строк и столбцов, ее называют квадратной. Обозначают матрицы большими латинскими буквами. Сами числа называют элементами матрицы и характеризуют их положением в матрице, задавая номер строки и номер столбца и записывая их в виде двойного индекса, причем вначале записывают номер строки, а затем столбца. Например, a14 есть элемент матрицы, стоящий в первой строке и четвертом столбце, a32 стоит в третьей строке и втором столбце. Главной диагональю квадратной матрицы называют элементы, имеющие одинаковые индексы, то есть те элементы, у которых номер строки совпадает с номером столбца. Побочная диагональ идет «перпендикулярно» главной диагонали. Особую важность представляют собой так называемые единичные матрицы. Это квадратные матрицы, у которых на главной диагонали стоят 1, а все остальные числа равны 0. Обозначают единичные матрицы E. Матрицы называют равными, если у них равны число строк, число столбцов, и все элементы, имеющие одинаковые индексы, равны. Матрица называется нулевой, если все ее элементы равны 0. Обозначается нулевая матрица О. Операция сложения определена ТОЛЬКО ДЛЯ МАТРИЦ ОДНОГО ПОРЯДКА. Другими словами, нельзя найти сумму матриц разной размерности и вообще нельзя говорить о сложении матриц разной размерности. Также нельзя говорить о сумме матрицы и числа или о сумме матрицы и какого-нибудь другого элемента. 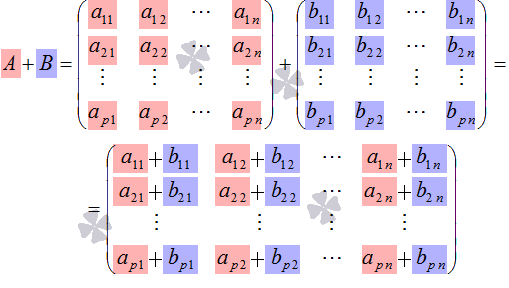 Определение операции умножения матрицы на число. Операция умножения матрицы на число определена ДЛЯ МАТРИЦ ЛЮБОГО ПОРЯДКА. Определение. Произведение матрицы 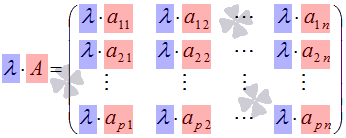 Таким образом, результатом умножения матрицы на число является матрица того же порядка. Операция умножения двух матриц А и В определяется только для случая, когда ЧИСЛО СТОЛБЦОВ МАТРИЦЫ А РАВНО ЧИСЛУ СТРОК МАТРИЦЫ В. Найдите все элементы матрицы С, которая получается при умножении матриц 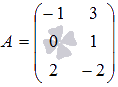 и и 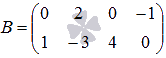 . .м случае, тогда 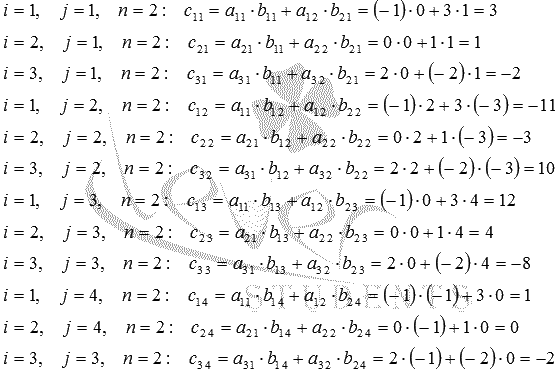 Определители 2-го и 3-го порядка. Определение и вычисление. определитель второго порядка равен произведению элементов на главной диагонали минус произведение элементов на побочной диагонали.  Свойства определителя n-ого порядка. Часто говорят также "определитель матрицы", поэтому сначала объясним, что такое матрица. Матрица - это прямоугольная таблица, составленная из чисел, которые нельзя менять местами. Квадратная матрица - таблица, у которой число строк и число столбцов одинаково. Определитель может быть только у квадратной матрицы. Итак, пусть дана квадратная таблица, состоящая из чисел, расположенных в nстроках (горизонтальных рядах) и в nстолбцах (вертикальных рядах). С помощью этих чисел по некоторым правилам, которые мы изучим ниже, находят число, которое и называют определителем n-го порядка и обозначают следующим образом: 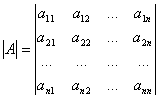 (1) (1)Числа Чтобы читателю был более понятен практический смысл составления матриц и определителей, упомянём один из многочисленных примеров. Если три магазина одной сети продают три различных вида товаров, то отчёт о продажах за год можно представить в виде таблицы из трёх строк и трёх столбцов, содержащей некоторые числа. Первый индекс каждого числа - это номер магазина, а второй - номер вида товара. Определители играют важную роль в решении систем линейных уравнений. А один из примеров, когда надо решить систему уравннений - вычисление величины факторов, влияющих на Ваше настроение. Здесь система линейных уравнений решается для получения коэффициентов линейной множественной регрессии, которые и являются измерением влияния. Свойство 1. При замене строк столбцами (транспонировании) значение определителя не изменится, т.е. 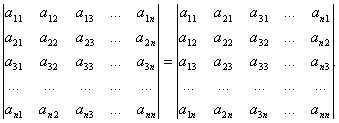 Свойство 2. Если хотя бы один ряд (строка или столбец) состоит из нулей, то определитель равен нулю. Доказательство очевидно. В самом деле, тогда в каждом члене определителя один из множителей будет нуль. Свойство 3. Если в определителе поменять местами два соседних параллельных ряда (строки или столбцы), то определитель поменяет знак на противоположный, т.е. 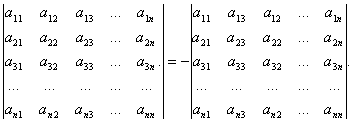 Свойство 4. Если в определителе имеются два одинаковых параллельных ряда, то определитель равен нулю: 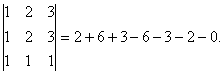 Свойство 5. Если в определителе два параллельных ряда пропорциональны, то определитель равен нулю: 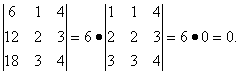 Свойство 6. Если все элементы определителя, стоящие в одном ряду, умножить на одно и то же число, то значение определителя изменится в это число раз: 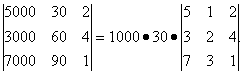 Следствие. Общий множитель, содержащийся во всех элементах одного ряда, можно вынести за знак определителя, например: 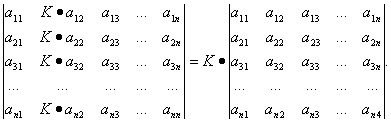 Свойство 7. Если в определителе все элементы одного ряда представлены в виде суммы двух слагаемых, то он равен сумме двух определителей: 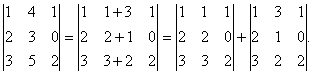 Свойство 8. Если к элементам какого-либо ряда прибавить произведение соответствующих элементов параллельного ряда на постоянный множитель, то значение определителя не изменится: 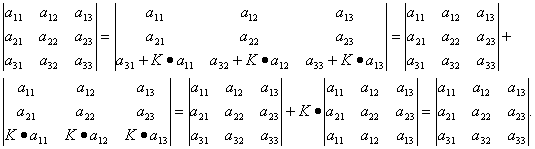 Свойство 9. Если к элементам i-го ряда прибавить линейную комбинацию соответствующих элементов нескольких параллельных рядов, то значение определителя не изменится: 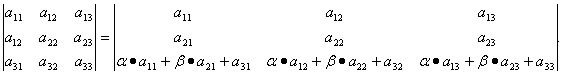 Справедливость этого равенства вытекает из свойства 8 Обратная матрица. Матрица А-1 называется обратной матрицей по отношению к матрице А, если А*А-1 = Е, где Е — единичная матрица n-го порядка. Обратная матрица может существовать только для квадратных матриц. Алгоритм нахождения обратной матрицыОпределяют, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует. Вычисление определителя матрицы A. Если он не равен нулю, продолжаем решение, иначе - обратной матрицы не существует. Нахождение транспонированной матрицы AT. Определение алгебраических дополнений. Заменяют каждый элемент матрицы его алгебраическим дополнением. Составление обратной матрицы из алгебраических дополнений: каждый элемент полученной матрицы делят на определитель исходной матрицы. Результирующая матрица является обратной для исходной матрицы. Делают проверку: перемножают исходную и полученную матрицы. В результате должна получиться единичная матрица. Системы линейных уравнений. Квадратные системы. Методы решения. 6. Произвольные системы линейных уравнений. Ранг системы. Теорема Кронекера-Капелли. Метод Жордана-Гаусса. 7. Векторы, действия над ними. Скалярное, векторное и смешанное произведения векторов, и их геометрические приложения. 8. Метод координат на плоскости. Уравнения прямой на плоскости. 9. Уравнение прямой и плоскости в трёхмерном пространстве. 10. Кривые второго порядка (эллипс, гипербола, парабола). 11. n – мерные векторы. Аксиоматическое определение n – мерного векторного пространства. 12. Функция и способы ее задания. 13. Предел функции в точке. Предел функции на бесконечности. 14. I-й и II-й замечательные пределы. Эквивалентные бмф. 15. Понятие неопределенности при нахождении предела. Методы разрешения неопределенностей. 16. Непрерывность функции. Точки разрыва. Классификация разрывов. 17. Понятие производной. Геометрический и экономический смысл производной. Связь непрерывности и дифференцируемости функций. 18. Дифференциал. Определение и геометрический смысл дифференциала функции в точке. Применение дифференциала к приближенным вычислениям. 19. Построение графиков функций. 20. Функция двух переменных. Частные производные функции двух переменных. 21. Неопределенный интеграл. 22. Свойства неопределенного интеграла. Таблица неопределенных интегралов. Методы интегрирования. 23. Определенный интеграл, его геометрический смысл. Свойства определенного интеграла. Формула Ньютона-Лейбница. 24. Дифференциальные уравнения первого порядка. 25. Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Теорема о структуре общего решения. 2 семестр Вопросы к экзамену 1. Понятие вероятности. Вероятностное пространство. Алгебра событий. 2. Классическая и дискретная схемы вероятностного пространства. 3. Геометрическая и непрерывная схемы вероятностного пространства. 4. Несовместность событий. Независимость событий. Условная вероятность. 5. Правила сложения и умножения вероятностей. 6. Формула полной вероятности. Формула Байеса. 7. Последовательность испытаний. Схема Бернулли. 8. Понятие случайной величины (СВ). Закон распределения. Функция распределения. Числовые характеристики СВ. 9. Дискретные СВ. Основные дискретные распределения. 10. Математическое ожидание СВ. Определение и свойства. 11. Дисперсия и среднеквадратическое отклонение СВ. Определение и свойства. 12. Неравенство Чебышева. Локальная и интегральные формулы Лапласа. 13. Закон больших чисел. Центральная предельная теорема. 14. Математическая модель задачи математического программирования. 15. Графический метод решения задач линейного программирования. 16. Симплексный метод решения задач линейного программирования. 17. Метод искусственного базиса. 18. Теория двойственности. 29. Транспортная задача линейного программирования. |
