Пнрррм. теория ВышМат. 1. Понятие матрицы. Виды матрицы. Матрица

• Название: 1. Понятие матрицы. Виды матрицы. Матрица
• Анкор: Пнрррм
• Дата: 09.12.2022
• Размер: 105.27 Kb.
• Имя файла: теория ВышМат.docx
• Тип: Документы; #835564
• страница: 1 из 5

1.Понятие матрицы. Виды матрицы.

Матрица- прямоугольная таблица действительных чисел , содержащая m строк и n столбцов.

Числа а₁₁, а₁₂, а₁₃ называются элементами матрицы. Каждый элемент а_ij снабжён двумя индексами: первый указывает на номер строки, второй- номер столбца, в которых расположен этот элемент. Матрицы обозначаются заглавными буквами (А,В,С)

1) Матрица, у которой m=n, называется квадратной. Элементы квадратных матриц, стоящие на диагонали, идущей с верхнего левого угла, образуют главную диагональ. Элементы квадратных матриц, стоящие на диагонали, идущей с верхнего правого угла, образуют побочную диагональ.

2) Квадратная матрица называется диагональной, если у неё ненулевыми элементами являются лишь элементы главной диагонали.

3) Квадратная матрица называется симметрической, если её элементы симметричные относительно главной диагонали, равны.

4) Матрица, все элементы которой равны 0, называется нулевой.

5) Если все ненулевые элементы диагональной матрицы равны 1, то такая квадратная матрица называется единичной.

6) Квадратная матрица, у которой все элементы, лежащие ниже( или выше) главной диагонали, равны 0, называется треугольной

7)Матрицу, состоящую из одной строки и n столбцов, называют иногда матрицей-строкой и аналогично матрицей -столбцов.

8) Две матрицы А и В называются равными, если они: а) имеют одинаковые размеры; б) соответствующие элементы матрицы равны

2. Умножение матрицы на число, сложение матриц. Свойства этих операций.

Умножение матрицы на число.

Произведение матрицы А_mxn=(a_ij) на действительное число а называется матрица, каждый элемент которой получается умножением соответствующего элемента матрицы А на число а

Сложение матриц.

Сложение матриц вводится только для матриц одинаковых размеров. Суммой мтариц А_mxn=(a_ij) и Bmxn=(b_ij) называется матрица Cmxn=(cij), элементы которой есть cij=aij+bij.

Свойства сложения и умножения матриц на число:

1. А+В=В+А

2. а(А+В)=а*А+а*В

3. (А+В)+С=А+(В+С)

4. (а+b)*A=a*A+b*A

5. (a*b)*A=(a*A)*b

6. Amxn+Omxn=Amxn

7. 0*Amxn=Omxn

3. Умножение матриц. Свойства операции умножения матриц.

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведение матрицы Amxn=(a_ij) на матрицу Bnxp=(b_jk) называется матрица Cmxp=(c_ij), такая что c_ik=a_i1b_1k+a_i2b_2k+….

Т.е. элемент i-ой строки и k-го столбца матрицы произведения С равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы k-го столбца матрицы В

Свойства произведений матриц:

1. Если А и В- квадратные матрицы одного размера, то АВ и ВА существуют. Степени квадратной матрицы определяются очевидным образом Ак=А*..*А, где к-целое число, А- квадратная матрица. 2 A*(BC)=(AB)*C

3. (A+B)*C=AC+BC

4. a*(AB)=(a*A)*B

5. Роль единичной (квадратной) матрицы: умножение слева, справа на данную матрицу не изменяют исходную матрицу

Emxn*Amxn=Amxn

6. Роль нулевой матрицы

(Omxn*Amxn=Omxn

4. Транспонирование матриц. Свойства операции транспонирования.

Матрица, строками которой являются столбцы матрицы А с тем же номером и сохранением порядка следования элементов, называется транспонированной к данной и обозначается как А^Т или А’

Свойства операции транспонирования:

1. (A^T)^T=A

2. (AB)^T=A^T*B^T

3. (A+B)^T=A^T+B^T

4.(a*A)^T=a*A^T

5. Определители квадратных матриц первого, второго и третьего порядков.

Определителем квадратной матрицы А n-го порядка называется алгебраическая сумма n!=1*2…n произведений n-го порядка элементов этой матрицы, причём в каждое произведение входит по одному элементу из каждой строки и каждого столбца данной матрицы. Знак каждого слагаемого определяется с помощью подсчёта так называемых инверсий в перестановке чисел (1,2..n)

Квадратная матрица первого порядка состоит из одного элемента, поэтому её определитель равен самому элементу 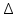=Ia₁₁I=a₁₁

Квадратная матрица 2-го порядка: определитель равен разности произведений элементов, стоящих на главной и побочной диагонали

= a11*a22- a12a21

Определитель 3-го порядка вычисляется при помощи правила треугольника(правило Саррюса)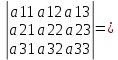

a11a22a33+a12a23a31+a13a21a32- a13a22a31-a12a21a33-a11a23a32

6. Определитель квадратной матрицы порядка n.

7. Свойства определителей.

1. Определитель матрицы, полученной из данной транспонированием, равен определителю данной матрицы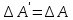

2. При перестановке местами двух строк ( столбцов) определитель меняет знак на противоположный, сохраняя при этом свою абсолютную величину.

3. Определитель с двумя одинаковыми строками (столбцами) равен нулю.

4. Если все элементы некоторой строки (столбца) определителя умножить на одно и то же число, то сам определитель умножится на это число.

Следствие 1. Общий множитель элементов любой строки (столбца) можно выносить за знак определителя

Следствие 2. Если определитель содержит нулевую строку (столбец), то он равен 0.

Следствие 3. Определитель с двумя пропорциональными строками ( столбцами) равен нулю.

5. Если каждый элемент i-строки( к-го столбца) определителя есть сумма двух слагаемых : a_ik=a’_ik+a’’_ik, то определитель есть сумма двух определителей; в первом из которых i-я строка(к-й столбец) состоит из элементов a’ik во втором- из элементов a’’_ik.

6. Определитель равен сумме произведений элементов какой-либо строки( столбца) определителя на их алгебраические дополнения.

7. Суммой произведений элементов какой-либо строки определителя на алгебраические дополнения соответствующих элементов другой строки равна нулю.

8. Если к элементам некоторой строки определителя прибавить элементы другой строки, умноженные на произвольное число а, то определитель не изменится.

9. Определитель произведения квадратных матриц одного порядка равен произведению определителей этих матриц.

8. Вычисление определителей методом элементарных преобразований.

Метод элементарных преобразований заключается в том, чтобы при помощи элементарных преобразований, учитывая св-ва определителей, привести матрицу к треугольному виду.

Под элементарными преобразованиями определителей матрицы понимаются следующие операции:

1.Перестановка местами двух строк или столбцов определителя: определитель изменяет свой знак на противоположный

2. Умножение элементов строки или столбцов на ненулевое число с: определитель умножается на число с

3.Прибивление к строке другой строки, предварительно умноженной на любое число: определитель не изменяется.

9. Понятия минора и алгебраического дополнения элемента квадратной матрицы. Теорема Лапласа о разложении определителя по строке ( столбцу).

Минор M_ij элемента a_ij- определитель , полученный в результате вычёркивания i-строки и j-го столбца матрицы.

Алгебраическим дополнением Аij элемента a_ij матрицы n-го порядка называется минор, взятый со знаком (-1)^i+j

Теорема Лапласа: Определитель матрицы равен сумме произведений элементов любой строки на их алгебраическое дополнение.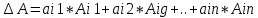

, где i- номер строки, 1≤ I ≤n

Эту формулу называют разложением определителя матрицы А по её i- строке. Аналогичная формула имеет место и для разложения определителя матрицы по её столбцу.

Теорема Лапласа сводит вычисление определителя матрицы n-го порядка к вычислению n по определителю матрицы (n-1)-го порядка. Например , определитель матрицы 4-го порядка можно найти путём разложения его по этой формуле, в которой будет четыре определителя матриц третьего порядка.

10. Обратная матрица, её свойства. Вычисление обратной матрицы.

Матрица А^-1 называется обратной к матрице А, если выполнено условие А^-1*А=АА^-1=E_nxm

Свойства обратной матрицы: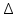

1. А^-1=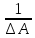

2. (А*В)^-1=В^-1А^-1

3. (А^Т)^-1=(А^-1)^Т

Алгоритм вычисления обратной матрицы:

1. Вычисляем определитель матрицы А

2. Вычисляем алгебраические дополнения всех элементов матрицы А и составляем из них присоединённую матрицу

3. Транспонируем присоединённую матрицу

4. Вычисляем обратную матрицу по формуле

А-1= 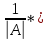А^Т

11. Минор к-го порядка матрицы. Ранг матрицы, его свойства.

Если взять любое число к, 1≤ к≤ min(m,n) и выделить в матрице А произвольным образом к строк и к столбцов, то элементы , которые находятся на пересечении выделенных строк и столбцов, будут образовывать квадратную матрицу к-го порядка. Определитель построенной матрицы называется минором к-го порядка матрицы А.

Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы.

Из этого определения вытекает, что если ранг матрицы равен r, то среди миноров этой матрицы есть по крайней мере один минор r-го порядка , отличный от нуля (его будем называть базисным минором), а все миноры порядка r+1 и выше раны нулю. Ранг матрицы А обозначается r(A). По определению ранг нулевой матрицы О равен нулю; тогда ранг r(A) произвольной матрицы удовлетворяет неравенству 0≤r(A)≤ min(m,n)

Свойства ранга матрицы:

1. При транспонировании матрицы ранг не меняется.

2. Если из матрицы вычеркнуть нулевой ряд, то ранг матрицы не изменится

3. Ранг матрицы не изменится при элементарных преобразований матрицы.

12. Вычисление ранга матрицы методом окаймляющих миноров.

Базисные миноры удобно находить по методу окаймляющих минором. Суть этого метода в следующем: если уже найден ненулевой минор к-го порядка, то другие миноры (к+1)-го порядка следует выбирать лишь такие , которые включают в себя целиком найденный на предыдущем шаге ненулевой минор к-го порядка. При больших размерах матриц такое «окаймление» существенно сократит число возможных переборов миноров (к+1)-го порядка.

13. Системы линейных алгебраических уравнений (СЛАУ). Основные понятия.

Линейным уравнением относительно неизвестных действительных чисел х₁,х₂…x_n, называется выражение вида:

A_1x1+a_2x2+…+a_nxn=b

Где а₁..a_n,b- заданные числа. При этом a₁,…a_n –называются коэффициентами уравнения, b- свободный член.

Основные определения:

Система называется совместной, если он имеет хотя бы одно решение, в противном случае- несовместной. Совместная система может иметь либо одно решение – её называют определённой, либо больше одного решения – её называют неопределённой.

Решить систему- значит выяснить, совместна она или несовместна , и в случае совместности найти все её решения.

Две системы называются эквивалентными , если они имеют одно и то же множество решений.

Два линейных уравнения называются равносильными, если множества их решения как множества совпадают.

14. Условие совместности СЛАУ (теорема Кронекера-Капелли)

Для формулировки теоремы Кронекера-Капелли вводится в рассмотрение расширенная матрица A_b системы. Она строится путём дополнения матрицы системы А столбцов свободных членов b.

Теорема: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы А равен рангу расширенной матрицы A_b.

Справедливо следующее утверждение , которое уточняет приведённую теорему:

Пусть система совместна и выполняется условие rA=rA_b=r Тогда:

1. При r=n (ранг равен числу неизвестных) система имеет единственное решение

2. При r
15. Правило решения произвольной СЛАУ ( структура общего решения)

1. Найти ранги основной и расширенной матрицы системы.

2. Если r(A)≠r 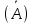, то система несовместна.

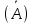3. Если r(A)=r =r , то система совместна.

4. Найти какой-либо базисный минор порядка r. Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные n-r неизвестных называют свободными и переносят в правые части уравнения.

5. Найти выражения главных неизвестных через свободные. Получить общее решение системы (множество всех решений)

6. Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных.

7. Таким образом можно найти частные решения исходной системы уравнений.

16. Невырожденные СЛАУ с квадратной матрицей коэффициентов. Матричный метод.

Матричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с n неизвестными. Тогда её можно переписать в матричной форме:

Ах=В, где А- основная матрица системы, В и Х- столбцы свободных членов и решений системы соответственно.

Умножим это матричное уравнение слева на А^-1 – матрицу обратную матрице А

А^-1*(АХ)=А^-1*В

Так как А^-1*А=Е, получаем Х=А^-1*В.

Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода является невырожденность матрицы А. Необходимым и достаточным условием этого является неравенство нулю определяителя матрицы А:

∆А≠0

18.Эквивалентные преобразования СЛАУ. Решение СЛАУ методом Гаусса. Базисные и свободные неизвестные.

Две системы вида называются эквивалентными, если они имеют одно и то же множество решений.

Элементарными преобразованиями исходной системы, которые приводят её к эквивалентным системам, являются:

1. Удаление из системы уравнений нулевой строки, т.е. уравнения вида 0_х1+0_х2+…+0_хn=0

2. Перестановка местами уравнений или слагаемых в уравнениях системы.

3. Прибавление к обеим частям одного уравнения соответственно обеих частей другого уравнения этой системы, умноженного на любое действительное число.

Метод Гаусса:

Метод Гаусса применяется для решения систем m линейных уравнений с n неизвестными, заданной в общем виде . Этот метод иначе называют методом последовательного исключения неизвестных.

В результате таких преобразований можно прийти к одному из двух случаев:

1. встретиться уравнение вида 0*x_k+…+0*x_n=g , где g≠0, т.е. рассматриваемая система несовместна

2. получится система ступенчатого вида



19. Системы линейных однородных уравнений. Общее решение однородных СЛАУ.

Система линейных уравнений называется однородной, если во всех уравнениях свободные члены равны 0, т.е. вектор =

Тогда однородная система в матричной форме имеет вид:

Ах=0, где матрица А=Аmxn составлена из коэффициентов системы

Очевидно, что верно равенство r(A)=r(A_b ). Значит, система всегда совместна. Очевидно, х=0 является решением , исходя из матричного вида.( тривиальное решение)

Теорема:

Для того, чтобы однородная система m линейных уравнений с n неизвестными, имела ненулевые решения необходимо и достаточно, чтобы r(A)
Теорема:

Для того, чтобы однородная система n линейных уравнений с n неизвестными, имела ненулевые решения, необходимо и достаточно, чтобы её определитель равнялся нулю:

∆А=0

Следствие:

Однородная система, у которой число уравнений меньше числа неизвестных всегда имеет ненулевое решение.