Пнрррм. теория ВышМат. 1. Понятие матрицы. Виды матрицы. Матрица
 Скачать 105.27 Kb. Скачать 105.27 Kb.
|
|
Структура общего решения однородной системы уравнений: Из теоремы следует, что r(A) Множество решений однородной системы линейных уравнений образует подпространство L пространства Rn, причём размерность L равна n-r , где r- ранг матрицы А. Совокупность линейно независимых решений системы А 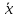 = =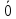 называют фундаментальной системой решений. называют фундаментальной системой решений.Таким образом, в пространстве решений L однородной системы существует базис из (n-r) штук n- мерных векторов-решений 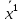 , ,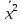 ,…, ,…,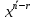 , таких, что любое решение , таких, что любое решение 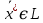 , т.е. решение однородной системы, есть линейная комбинация векторов , т.е. решение однородной системы, есть линейная комбинация векторов 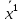 , ,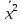 ,…, ,…,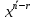 : :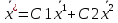 + +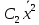 +…+ +…+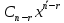 , где С1,С2,…,Сn-r- произвольные постоянные. При этом верхние индексы у векторов означают не показатели степени, а их порядковые номера. , где С1,С2,…,Сn-r- произвольные постоянные. При этом верхние индексы у векторов означают не показатели степени, а их порядковые номера.20. Понятие об n- мерном векторе. Арифметическое n- мерное векторное пространство. Любой упорядоченный набор из n-действительных чисел (х1, х2,…,хn) называется n-мерным вектором и обозначается 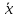 . Числа хi, i=1,…,n, составляющие упомянутый набор, называются компонентами (координатами) вектора . Числа хi, i=1,…,n, составляющие упомянутый набор, называются компонентами (координатами) вектора 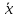 . .Вектора имеют свойства: Пусть 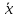 , ,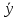 , ,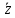 - произвольные n-мерные векторы. Тогда: - произвольные n-мерные векторы. Тогда:1) 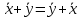 - переместительный закон( или коммутативность) - переместительный закон( или коммутативность)2) ( 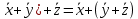 - сочетательный закон ( или закон ассоциативности относительно сложения) - сочетательный закон ( или закон ассоциативности относительно сложения)3) λ( 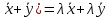 , где λ- это действительное число (дистрибутивный закон относительно сложения векторов) , где λ- это действительное число (дистрибутивный закон относительно сложения векторов)4) (λ+ 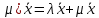 , где λ, μ- это действительные числа (дистрибутивный закон относительно сложения векторов) , где λ, μ- это действительные числа (дистрибутивный закон относительно сложения векторов)5) λ(μ 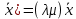 - ассоциативный закон относительно умножения на числа - ассоциативный закон относительно умножения на числа6) 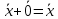 , где , где 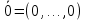 7) для любого вектора 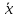 существует такой вектор (- существует такой вектор (-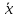 ), что ), что 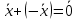 8) 1* 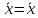 9) 0* 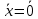 Совокупность всех n-мерных векторов с линейными операциями (сложение и умножение на действительное число), подчиняющиеся свойствам, называется n- мерным линейным ( или векторным) пространством. Если координаты векторов- действительные числа ,то пространство называется арифметическим и обозначается 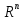 21. Линейная зависимость и независимость векторов. Основные свойства. Система векторов 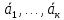 является линейно зависимой, если существуют такие числа является линейно зависимой, если существуют такие числа 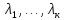 , из которых хотя бы одно отлично от нуля ( иногда этот факт записывают как , из которых хотя бы одно отлично от нуля ( иногда этот факт записывают как 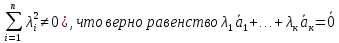 т.е.линейная комбинация векторов равна нулевому вектору. т.е.линейная комбинация векторов равна нулевому вектору.Если же равенство возможно лишь при λ1=λ2=…=λк=0, то такая система векторов называется линейно независимой. Простейшие свойства линейно зависимых и независимых векторов: 1) Нулевой вектор 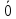 разлагается по любой системе векторов, так как справедливо равенство разлагается по любой системе векторов, так как справедливо равенство 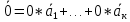 , с нулевыми коэффициентами. , с нулевыми коэффициентами.2)Если вектор разлагается по части векторов, взятых из заданной совокупности, то он разлагается и по всей системе векторов (дополняя остальные слагаемые ,например, нулевыми коэффициентами). 3)Каждый n-мерный вектор 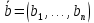 разлагается по следующей диагональной системе единичных n-мерных векторов: разлагается по следующей диагональной системе единичных n-мерных векторов: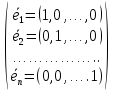 в виде в виде 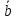 = =  4)Если система векторов зависима, то в сумме найдётся слагаемое, у которого λ≠0 , а значит , вектор 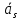 можно линейно выразить через остальные векторы (разделив все соотношения на можно линейно выразить через остальные векторы (разделив все соотношения на 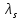 и перенося в другую часть) и перенося в другую часть)5) Система векторов, содержащая нулевой вектор, всегда линейно зависима. 6) Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны. Три 3-мерных вектора линейно зависимы тогда и только тогда, когда они компланарны. 7) Если система 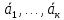 линейно независима, то и любая её подсистема линейно независима. линейно независима, то и любая её подсистема линейно независима.8) Наоборот, если в системе 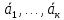 какая-то её часть линейно зависима, то вся система линейно зависима. какая-то её часть линейно зависима, то вся система линейно зависима. 22. Размерность и базис векторного пространства. Разложение n-мерного вектора по заданному базису. Координаты вектора в заданном базисе. Размерность векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве. Базисом системы векторов называют всякий набор векторов bi1, bi2,…,bik этой системы, удовлетворяющий следующим условиям: 1) векторы bi1, bi2,…,bik линейно независимы 2) любой вектор из совокупности векторов линейно выражается через векторы bi1,bi2,…,bik Векторы, входящие в базис, называют базисными. Любая система n-мерных векторов, число векторов в которой меньше n, не является базисом. Векторное пространство размерности n имеет столько базисов, сколько существует линейно независимых систем из n n-мерных векторов Пусть произвольные векторы е(1),е(2),…,е(n) являются базисом n-мерного векторного пространства. Если к ним добавить некоторый n-мерный вектор х, то полученная система векторов будет линейно зависимой. Из свойств линейной зависимости мы знаем, что хотя бы один вектор линейно зависимой системы линейно выражается через остальные. Иными словами, хотя бы один из векторов линейно зависимой системы раскладывается по остальным векторам. Теорема: Любой вектор n-мерного векторного пространства единственным образом раскладывается по базису. Коэффициенты х1, х2,…,хn называются координатами вектора х в базисе е(1),е(2),…,е(n) После знакомства с теоремой о разложении вектора по базису, мы начинаем понимать суть выражения «нам задан n-мерный вектор х=(х1,х2,…,xn)». Это выражение означает, что мы рассматриваем вектор х n-мерного векторного пространства, координаты х1,х2,…,xn которого заданы в некотором базисе. При этом мы понимаем, что этот же вектор х в другом базисе n-мерного векторного пространства будет иметь координаты, отличные от x1,x2,…,xn 23. Скалярное произведение векторов, его свойства. Евклидово пространство Скалярным произведением 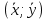 двух векторов двух векторов 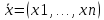 и и 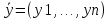 называется число, равное сумме произведений соответствующих (одноимённых) координат. называется число, равное сумме произведений соответствующих (одноимённых) координат.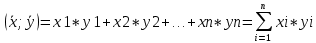 Основные св-ва скалярного произведения векторов: 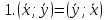 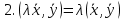 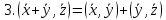 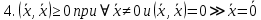 Векторное пространство с введённым в нём скалярным произведением называется евклидовым пространством. 24. Длина вектора. Угол между арифметическими векторами. Длиной n-мерного вектора 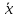 обладает длиной, причём нулевой вектора обладает длиной, причём нулевой вектора 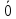 является единственным вектором, длина которого равна 0. является единственным вектором, длина которого равна 0.Иногда скалярное произведение 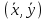 называют скалярным квадратом вектора называют скалярным квадратом вектора 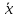 и обозначают х-2. Тогда из формулы длины вектора следует и обозначают х-2. Тогда из формулы длины вектора следует 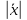 2 = 2 =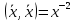 , т.е. квадрат длины вектора равен скалярному квадрату. Отсюда вытекает Теорема. , т.е. квадрат длины вектора равен скалярному квадрату. Отсюда вытекает Теорема.Теорема: Если 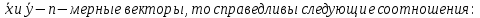 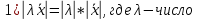 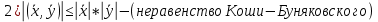 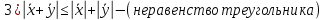 Следствие: вектор называется нормированным, если его длина равна 1 Из неравенства Коши-Буняковского следует двойное неравенство - 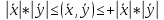 или если разделим его на или если разделим его на 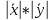 , то получим , то получим -1≤ 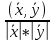 ≤1 ≤1Углом ф между ненулевыми n-мерными векторами 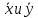 называется уравнение называется уравнениеCos ф= 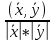 , которое принадлежит отрезку [0,п] , которое принадлежит отрезку [0,п]Из условия следует, что уравнение имеет на отрезке [0,п] единственное решение при любых 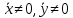 Следствие: Скалярное произведение равно произведению длин этих векторов на косинус угла между ними. 1) Два ненулевых n-мерных вектора 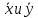 называются коллинеарными, если угол между ними равен 0 или п. Если ф=0, то векторы называют одинаково неправлеными, если ф=п, то противоположно направленными называются коллинеарными, если угол между ними равен 0 или п. Если ф=0, то векторы называют одинаково неправлеными, если ф=п, то противоположно направленными2) Два ненулевых n-мерных вектора 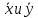 называются ортогональными, если их скалярное произведение равно нулю называются ортогональными, если их скалярное произведение равно нулю 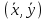 =0 (или угол между ними равен п/2) =0 (или угол между ними равен п/2)Теорема: Ненулевые векторы 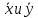 коллинеарны тогда и только тогда , когда можно найти такое число λ, что коллинеарны тогда и только тогда , когда можно найти такое число λ, что 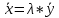 25. Прямая на плоскости. Уравнение прямой с угловым коэффициентом. Уравнение прямой, проходящей через заданную точку в заданном направлении. Уравнение прямой, проходящей через две заданные точки. Прямую на плоскости относительно фиксированной системы координат можно задать: 1) двумя различными её точками 2) точкой и направление (вектором) прямой 3) точкой прямой и вектором, перпендикулярным прямой. Общее уравнение прямой: Ах+Ву+С=0 Уравнение прямой с угловым коэффициентом: Под углом наклона прямой к оси Ох, понимают угол, отсчитываемый в направлении движения, противоположным движению часовой стрелки, от положительного направления оси х до данной прямой. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом этой прямой и обозначается k. 1) Если прямая параллельна оси Ох, то к=0. Если прямая перпендикулярна оси Ох , то к не существует 2) Если известен угловой коэффициент к и величина b отрезка, отсекаемого прямой на оси Оу, то для произвольной точки М (х,у) этой прямой у=кх+b Уравнение прямой с заданным угловым коэффициентом к и проходящей через заданную точку М0=(х0,у0) Искомое уравнение L имеет вид у=кх+b. Но т.к. M0 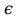 L , то её координаты удовлетворяют данному уравнению. Значит у0=кх0+b0. Вычитая это из предыдущего уравнения, имеет у-у0=к(х-х0) L , то её координаты удовлетворяют данному уравнению. Значит у0=кх0+b0. Вычитая это из предыдущего уравнения, имеет у-у0=к(х-х0)Уравнение прямой L , проходящей через две заданные токи Пусть заданы М1(х1,у1) и М2(х2,у2), причём х1≠х2. Т.к. М1 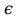 L , то L имеет вид у-у1=к(х-х1). Но этой же прямой должна принадлежать и точка М2. Следовательно М2 удовлетворяет последнему уравнению: у-у1=к(х-х1)—у2-у1=к(х2-х1). Отсюда к= L , то L имеет вид у-у1=к(х-х1). Но этой же прямой должна принадлежать и точка М2. Следовательно М2 удовлетворяет последнему уравнению: у-у1=к(х-х1)—у2-у1=к(х2-х1). Отсюда к=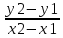 . Подставляем найденный коэффициент в уравнение у-у1=к(х-х1) имеет у-у1= . Подставляем найденный коэффициент в уравнение у-у1=к(х-х1) имеет у-у1=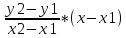 . Если разделим на (у2-у1) (при условии у2≠у1), то имеем в итоге: . Если разделим на (у2-у1) (при условии у2≠у1), то имеем в итоге: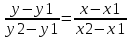 26. Уравнение прямой в отрезках. Общее уравнение прямой на плоскости. Пусть прямая отсекает на осях координат Ох и Оу отрезки а≠0, b≠0, соответственно. Тогда легко видеть, что точки пересечения прямой с осями координат есть М1(а;0), М2(0;b). Составим теперь уравнение прямой, проходящей через данные точки пересечения М1(а;0),М2(0;b). Имеем 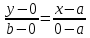 или или 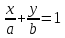 - уравнение прямой в отрезках - уравнение прямой в отрезкахОбщее уравнение прямой: Ах+Ву+С=0 , где А,В,С- числа, А2+В2≠0 1. Если А=0, В≠0 уравнение прямой принимает вид: у=у1, прямая параллельна оси Ох, угловой коэффициент равен 0 2. Если А≠0, В=0 уравнение прямой принимает вид: х=х1, прямая параллельна оси Оу, углового коэффициента не имеет 3. Если А≠0,В≠0, то уравнение прямой принимает вид: у=кх=b, где к= 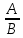 27. Угол между прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых. Углом между двумя прямыми называется любой из двух углов, образованных прямыми при их пересечении Пусть ф(0≤ф≤п)- угол между прямыми l1и l2, которые задаются уравнениями у=л1х+b1 и у=к2х+b2 , соответственно, где к1=tg a1 и к2=tg a2. Тогда а2=а1+ф. Откуда ф=ф2-ф1. Тогда, пользуясь формулами тригонометрии , имеем Tg ф= tg(a2-a1)= 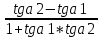 Или tg ф= 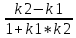 Если прямые параллельны, то ф=0 и tgф=0 – к2-к1=0, т.е.к1=к2 И наоборот, если к2=к1 то ф=0, т.е. прямые параллельны. Таким образом, необходимым и достаточным условием параллельности двух прямых является условие к2=к1- равенство угловых коэффициентов.( 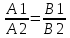 - условие параллельности) - условие параллельности)Если прямые перпендикулярны, т.е. ф= 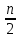 , то , то а2= 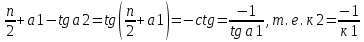 или к2*к1=-1. И наоборот: если к2*к1=-1, то из формулы tg ф=  следует ф= следует ф= , то прямые перпендикулярны. , то прямые перпендикулярны.Таким образом, для перпендикулярности прямых необходимо и достаточно, чтобы выполнялось равенство к2=  ( А1А2+В1В2=0 – условие перпендикулярности) ( А1А2+В1В2=0 – условие перпендикулярности)Т.е. угловые коэффициенты взаимно- обратны с противоположным знаком. |
