Пнрррм. теория ВышМат. 1. Понятие матрицы. Виды матрицы. Матрица
 Скачать 105.27 Kb. Скачать 105.27 Kb.
|
|
36. Бесконечно малые и бесконечно большие функции. Функция f(x) называется бесконечно малой величиной, если при х 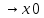 или при х или при х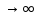 её предел равен 0. её предел равен 0.Теорема: Если функция f(x) имеет при х→х0 или при х→∞ предел, равный А, то её можно представить в виде суммы этого числа А и бесконечно малой величины а(х) при х→х0 или х→∞ 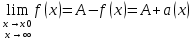 Верна и обратная теорема: Если функцию f(x) можно представить как сумму числа А и бесконечно малой величины а(х) при х→х0 или х→∞, то число А является пределом этой функции при х→х0 или при х→∞ F(x)=A+a(x) - 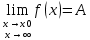 Свойства бесконечно малых величин: 1. Алгебраическая сумма бесконечно малых величин есть величина бесконечно малая. 2. Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая 3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от 0, есть величина бесконечно малая. Замечание: Предел отношения двух бесконечно малых величин 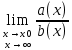 1. может быть равен нулю, тогда а(х) называется бесконечно малой более высокого порядка, чем b(x) 2. Может быть равен числу А, не равному нулю, тогда а(х) и b(x) имеют одинаковый порядок малости. 3. может быть равен бесконечности, тогда а(х) называется бесконечно малой более низкого порядка, чем b(x) Функции f(x) называется бесконечно большой величиной, если для любого, даже сколь угодно большого числа М˃0 найдётся такое число 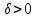 , что для всех х≠х0 и удовлетворяющих условию , что для всех х≠х0 и удовлетворяющих условию 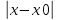 < <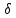 выполняется неравенство выполняется неравенство 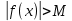 Если f(x) 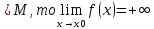 Если f(x) 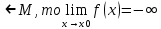 Замечание: Бесконечно большая величина является неограниченной функцией при х→х0 или при х→∞, но в то же время неограниченная функция не обязательно бесконечно большая. Свойства бесконечно больших величин: 1. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая. 2. Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая. 3. Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая. 37. Основные теоремы о пределах. Теорема 1. Функция не может иметь более одного предела. Теорема 2. Предел алгебраической суммы ( разности) конечного числа функций равен сумме (разности) пределов этих функций: 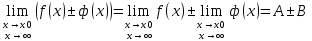 Теорема 3. Предел произведения конечного числа функций равен произведению пределов этих функций: : 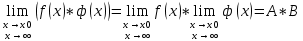 Следствие: 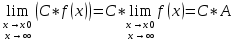 Теорема 4. Предел частного двух функций равен частному пределов этих функций: 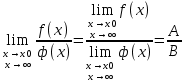 Теорема 5. Если 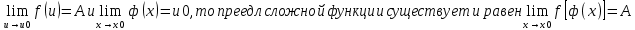 Теорема 6. Если в некоторой окрестности точки х0 (или при достаточно больших х) f(x)<ф(x), то 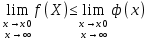 Признаки существования пределов Теорема 1. Если числовая последовательность 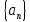 монотонна и ограничена, то она имеет предел . монотонна и ограничена, то она имеет предел .Возможны 2 случая: 1. Последовательность не убывает и ограничена сверху: а1≤а2≤…≤an≤М 2. Последовательность не возрастает и ограничена снизу: m≥a1≥a2≥…≥an Теорема 2. Если в некоторой окрестности точки х0 (или при достаточно больших значениях х) функция f(x) заключена между двумя функциями ф(х) и w(x), имеющими одинаковый предел, равный А, то функция f(X) имеет тот же предел А 38. Первый и второй замечательный пределы. Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере. 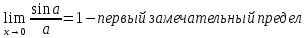 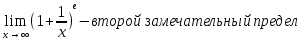 39. Непрерывность функции в точке. Точки разрыва функции и их классификация. Функция y=f(X) называется непрерывной в точке х=х0 слева (справа) , если f(x0-0)=  Отсюда следует, что непрерывность функции можно определить ещё так: функция f(x) непрерывна в точке х=х0, если она определена в этой точке и её окрестности и f(x0)=f(x0-0)=f(x0+0) Точка х0 называется точкой разрыва функции y=f(x) , если функция в этой точке не определена, или же не является в ней непрерывной (т.е. предел f(x) в точке х0 либо не существует, либо существует , но не равен f(x0)!) Точка х0 называется точкой разрыва 1 рода функции, если в этой точке существует f(x0-x) и f(x0+x) но f(x0-0)≠f(x0+0). При этом величина разности f(x0+0)-f(x0-0) называется скачком функции в точке х0. Точка х0 называется точкой устранимого разрыва, если f(x0-0)=f(x0+0)≠f(x0) (либо f(x) не определена в точке х0). Следовательно, чтобы устранить разрыв в точке х0 достаточно положить f(x0)=f(x0 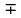 0)=f(x0+0) ,т.е. надо изменить значение функции в одной точке. 0)=f(x0+0) ,т.е. надо изменить значение функции в одной точке.Точка х0 называется точкой разрыва 2 рода, если в этой точке функция f(x) либо не имеет по крайней мере одного из односторонних пределов, либо хотя бы один из односторонних пределов является бесконечным. 40. Теоремы о непрерывности функциях. Функция f(x) называется непрерывной на отрезке [a,b] , если она непрерывна в каждой точке х 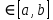 этого отрезка (при этом в точке х=а непрерывна справа, а в точке х=b непрерывна слева) этого отрезка (при этом в точке х=а непрерывна справа, а в точке х=b непрерывна слева) Непрерывные функции обладают рядом замечательных свойств. Теорема (первая теорема Вейерштрасса) Непрерывная на отрезке [a,b] функция является ограниченной функцией. Теорема (вторая теорема Вейерштрасса) Непрерывная на отрезке [a,b] функция достигает на этом отрезке своего наибольшего и наименьшего значений (не обязательно единственны) Теорема (Больцано-Коши о промежуточном значении) Если f(x) непрерывна на [a,b] и f(a)=A , f(b)=B, (A≠B), A Следствие: Если f(x) непрерывна на [a,b] и на концах отрезка принимает значение разных знаков, то 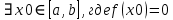 41. Свойства функций, непрерывных на отрезках. 1. Если функция f(x) и ф(х)- непрерывны в точке х0, то их сумма, разность, произведение и частное тоже являются функциями, непрерывными в точке х0 2. Если функция f(X) непрерывна в точке х0 и f(x0)˃0, то существует такая окрестность точки х0, в которой f(x0)˃0 3. Если функция y=f(u) непрерывна в точке u0, а u=ф(х) непрерывна в точке х0, причём u0=ф(х0), то сложная функция y=f(ф(x)) непрерывна в точке х0. 42. Производная функции, её геометрический, механический и экономический смысл. Эластичность функции. Производной функции y=f(x) в точке х называется предел отношения приращения функции к приращению независимого аргумента, когда приращение аргумента стремится к нулю. 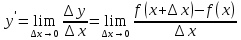 Геометрический смысл производной: Производная f’(x0) есть угловой коэффициент (тангенс угла наклона) касательной, проведённой к кривой y=f(x) в точке х0: K=f’(x0) Механический смысл производной: Производная пути по времени S’(t0) есть скорость точки в момент времени t0: V(t0)=S’(t0) Экономический смысл производной: Производная объёма производимой продукции по времени v’(t0) есть производительность труда в момент времени t0: z(t0)=v’(t0) В экономике широко применяют анализ относительных изменений, называемый ещё вычислением эластичности функций. Эластичностью функции y=f(x) называется предел относительного приращения функции к относительному приращению аргумента функции, если приращение аргумента стремится к 0 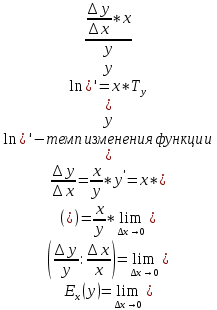 Эластичность позволяет измерять степень чуткости или чувствительности, например к изменению цены продукции. 43. Связь между непрерывностью и дифференцируемостью функции. При определении производной мы предполагали: 1) существование f(x) в точке х0 и её окрестности 2) существование предела 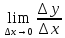 Теорема: Если функция дифференцируема, то она непрерывна Замечание: Обратное утверждение неверно. А) Существует функции, которые во всей области определения (т.е. везде) являются разрывными. Б) Существуют непрерывные функции, везде не имеющие производной. 44. Основные правила дифференцирования. Таблица производных. Процесс нахождения производной функции f(x) называется дифференцированием функции. Основные правила: 1. Если функция u=u(x) и v=v(x) дифференцируемы в точке х0, то функции : cu, u  v, v,  (v≠0 – в окрестности точки х0), являются также дифференцируемы в точке х0, причём справедливы следующие формулы: (cu)’=c*u’, (u (v≠0 – в окрестности точки х0), являются также дифференцируемы в точке х0, причём справедливы следующие формулы: (cu)’=c*u’, (u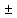 v)’=u’ v)’=u’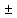 v’ , (u*v)’=u’v+uv’ , v’ , (u*v)’=u’v+uv’ , 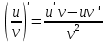 2.Дифференцирование сложных функций. Если функция z=ф(х) имеет производную в точке х0 равную 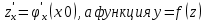 Имеет в соответствующей точке z0=ф(х0) производную 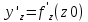 , то сложная функция y=f(ф(х)) имеет производную , то сложная функция y=f(ф(х)) имеет производную 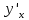 в точке х0 равную в точке х0 равную 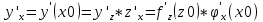 3. Дифференцирование обратной функции. Если для функции y=f(x) , x 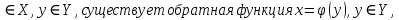 которая в точке которая в точке 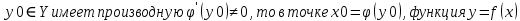 имеет производную f’(x0) , равную имеет производную f’(x0) , равную 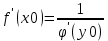 4. Дифференцирование простых функций. 5. Дифференцирование функций, заданных параметрически. Пусть зависимость переменной у и переменной х задана в параметрическом виде: Х=ф(t) , y=w(t) , t0≤t≤ 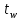 Тогда 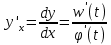 6. Логарифмическая производная. Пусть y=f(x)˃0- некоторая функция. Образуем функцию ln y и вычислим её производную (ln y)’= 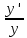 , которая называется логарифмической производной. , которая называется логарифмической производной.Отношение 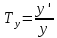 называется темпом роста функции или по другому, относительной скоростью изменения функции y=f(x) называется темпом роста функции или по другому, относительной скоростью изменения функции y=f(x)7. Таблица производных простейших элементарных функций. 8. Производные высших порядков. Если функция y=f(x), x  является дифференцируемой для является дифференцируемой для  , то её производная y’=y’(x)=g(x), x , то её производная y’=y’(x)=g(x), x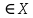 является новой функцией y=g(x) от переменной х и можно опять ставить вопрос о её дифференцировании. является новой функцией y=g(x) от переменной х и можно опять ставить вопрос о её дифференцировании. Производная от производной y’=f’(x) называется второй производной и обозначается 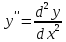 . .45. Производная сложной функции. Производная обратной функции. Сложная функция: y=f[ф(х)] Теорема: Если y=f(u) , u=ф(х)- дифференцируемые функции своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу, умноженной на производную самого промежуточного аргумента по независимой переменной: y’=f’(u)*u’x Правило дифференцирования сложной функции можно записать так: 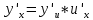 или или 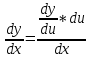 Пусть y=f(x) – дифференцируемая и монотонная функция на промежутке Х Если переменную у рассматривать, как аргумент, а переменную х как функцию , то функция х=ф(у) является обратной функцией к данной, непрерывной на соответствующем промежутке Y. Теорема: Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной исходной функции: 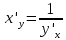 Эта формула имеет простой геометрический смысл. Если у’x есть тангенс угла наклона касательной к кривой y=f(X) к оси абсцисс, то x’y есть тангенс угла наклона той же касательной к оси ординат. 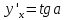 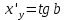 Причём  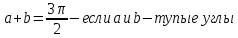 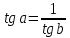 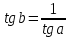 46. Производная степенно- показательной функции. Y=(f(x))ф(х) Логарифмируем обе части равенства по основание е: 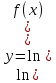 Дифференцируем обе части равенства по х, учитывая, что в правой части стоит произведение: 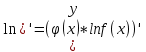 . Окончательно получаем . Окончательно получаем 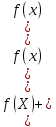 Чтобы продифференцировать степенно-показательную функцию, её сначала нужно продифференцировать как показательную функцию , а затем как степенную и полученную результаты сложить. Производная логарифмичекой функции: (ln y)’= 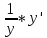 называется логарифмической производной. Её удобно использовать для дифференцирования функции, выражение которой существенно упрощается при логарифмирования. называется логарифмической производной. Её удобно использовать для дифференцирования функции, выражение которой существенно упрощается при логарифмирования. 47. Дифференцирование неявной функции. F(x,y)=0 Для нахождения производной неявной функции надо продифференцировать обе части уравнения, рассматривая у как функцию от х. Затем из полученного уравнения выразить у’. Пример: 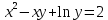 Дифференцируем обе части уравнения по х: 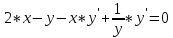 Выражаем отсюда искомую производную: 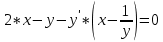 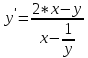 48. Производные высших порядков. Производной n-го порядка называется производная от производной n-1-го порядка F’’(x)- производная 2-го порядка F’’’(x)-производная 3-го порядка F(4)(x)-производная 4-го порядка F(n)(x)-производная n-го порядка |
