Пнрррм. теория ВышМат. 1. Понятие матрицы. Виды матрицы. Матрица

• Название: 1. Понятие матрицы. Виды матрицы. Матрица
• Анкор: Пнрррм
• Дата: 09.12.2022
• Размер: 105.27 Kb.
• Имя файла: теория ВышМат.docx
• Тип: Документы; #835564
• страница: 5 из 5

Механический смысл второй производной.

Если точка движется прямолинейно по закону S=S(t), то S’(t₀) – есть скорость изменения пути в момент времени t₀

Следовательно, вторая производная по времени S’’(t₀)=(S’(t₀))’=v’(t₀) –есть скорость изменения скорости, или ускорение, в момент времени t0

49. Теорема Ферма, теорема Ролля. Их геометрический смысл.

Теорема Ферма (о равенстве нулю производной)

Пусть функция y=f(x):

1) дифференцируема на интервале (a;b)

2) достигает экстремума в точке х₀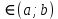

Тогда производная в этой точке равна 0: f’(x₀)=0

Геометрический смысл: в точке наибольшего или наименьшего значения касательная к графику функции параллельна оси абсцисс.

Теорема Ролля ( о производной функции, принимающей на концах отрезка равные значения) .

Пусть функция y=f(X)

1) непрерывна на отрезках [a;b]

2) дифференцируема на интервале (a;b)

3) на концах отрезка [a;b] принимает равные значения: f(a)=f(b)

Тогда на интервале (a;b) найдётся по крайней мере одна точка х₀, в которой f’(x₀)=0

Геометрический смысл: найдётся хотя бы одна точка, в которой касательная к графику функция будет параллельна оси абсцисс.

50. Теорема Лагранжа о конечных приращениях, её геометрический смысл.

Пусть функция y=f(X)

1) непрерывна на отрезке [a;b]

2) дифференцируема на интервале (a;b)

Тогда на интервале (a;b) найдётся по крайней мере одна точка х₀ такая, что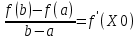

Геометрический смысл: Отношение 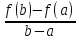есть угловой коэффициент хорды АВ, а f’(X₀) есть угловой коэффициент касательной к кривой y=f(x) в точке с абсциссой х₀. Утверждение теоремы Лагранжа сводится к следующему: на кривой y=f(X) точка М(х₀;f(x₀))такая, что через эту точку можно провести касательную, параллельную хорде АВ.

Формула Лагранжа или формула конечных приращений: f(b)-(a)=f’(x0)*(b-a)

51. Правило Лопиталя раскрытия неопределённостей.

Теорема: Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному)

Т.е. если существует предел вида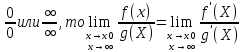

52. Достаточное условие возрастания ( убывания) функции.

Теорема 1( достаточное условие возрастания функции) : Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то функция возрастает на этом промежутке.

Теорема 2( достаточное условие убывания функции): Если производная дифференцируемой функции отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке.

Геометрическая интерпретация: Если касательная к кривой на некотором промежутке направлены под острыми углами к оси х, то функция возрастает. Если она направлена под тупыми углами, то функция убывает

53. Экстремумы функции. Необходимое условие экстремума функции.

Точка х₀ называется точкой максимума функции f(x), если в некоторой окрестности точки х₀ выполняется неравенство: f(X)≤f(x₀)

Точка х₁ называется точкой минимума функции f(X), если в некоторой окрестности точки х₁ выполняется неравенство: f(X)≥(f(X₁)

Значения функции в точках х₀ и х₁ называются соответственно максимум и минимумом функции.

Максимум и минимум функции называется экстремумом функции.

На одном промежутке функция может иметь несколько экстремумов, причём может быть, что минимум в одной точке больше максимума в другой.

Если в некоторой точке х₀ дифференцируемая функция f(X) имеет экстремум, то в некоторой окрестности этой точки выполняется теорема Ферма и производная функции в этой точке равна нулю: f’(x₀)=0

Однако, функция может иметь экстремум в точке, в которой она не дифференцируема. Например, y= 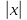имеет минимум в точке х=0, но она в этой точке не дифференцируема.

Необходимое условие экстремума: Для того , чтобы функция y=f(X) имела экстремум в точке х0, необходимо, чтобы её производная в этой точке равнялась нулю или существовала.

Точки, в которых выполняется необходимое условие экстремума, называются критическими или стационарными.

Таким образом, если в какой-либо точке имеется экстремум, то эта точка является критической. Но критическая точка не обязательно является точкой экстремума.

54. Достаточное условие (первое и второе) экстремума функции

1 условие: Если при переходе через точку х₀ производная дифференцируемой функции f(X) меняет знак с + на - , то х₀ есть точка максимума, а если с – на + , то х₀ есть точка минимума.

Схема исследования функции на экстремум:

1. Найти производную функции y’=f’(x)

2. Найти критические точки функции, в которых производная равна нулю или не существует.

3. Исследовать знак производной слева и справа от каждой критической точки

4. Найти экстремум функции

2 условие: Если первая производная дифференцируемой функции f(X) в точке х₀ равна 0, а вторая производная в этой точке положительна, то х0 есть точка минимума, а если вторая производная отрицательна, то х₀ есть точка максимума.

Схема исследования функции на экстремум:

1. Найти производную функции y’=f’(x)

2. Найти критические точки функции, в которых производная равна нулю или не существует.

3. Найти вторую производную и определить её знак в каждой критической точке.

4. Найти экстремум функции

Из второго достаточного условия следует, что если в критической точке вторая производная функции не равна нулю, то эта точка является точкой экстремума. Обратное утверждение не верно: если в критической точке вторая производная функции равна нулю, то эта точка также может являться точкой экстремума.

В этом случае для исследования функции необходимо использовать первое достаточное условие экстремума.

55. Нахождение наибольшего и наименьшего значений функции на отрезке.

Согласно теореме Вейерштрасса , если функция непрерывна на отрезке [a;b] , то она достигает на нём наибольшего и наименьшего значений.

Эти значения могут быть достигнуты на концах отрезка или в точках экстремума

Схема нахождения наибольшего и наименьшего значения функции на отрезке:

1. Найти производную функции

2. Найти критические точки, в которых производная равна нулю или не существует

3. Найти значения функции в критических точках и на концах отрезка, и выбрать из них наибольшее и наименьшее значения

Замечание: Если функция непрерывна на интервале (a;b), то она может не принимать на нём наибольшее и наименьшее значения. В частности, если дифференцируемая функция y=f(X) на интервале (a;b) имеет лишь одну точку максимума ( или минимума), то наибольшее (или наименьшее ) значение функции совпадает с максимумом (минимумом) этой функции.

56. Выпуклость и вогнутость функции. Достаточное условие выпуклости (вогнутости) функции. Точки перегиба функции. Необходимое и достаточное условие перегиба функции.

Функция y=f(x) называется выпуклой вниз (вогнутой) на промежутке Х, если для любых х1,х2 из этого промежутка выполняется неравенство: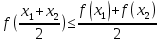

Функция y=f(X) называется выпуклой вверх на промежутке Х, если для любых х1,х2 из этого промежутка выполняется неравенство: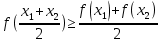

Теорема 1: Функция выпукла вверх (вниз) на промежутке Х тогда и только тогда, когда её первая производная на этом промежутке монотонно возрастает (убывает)

Теорема 2(достаточное условие выпуклости функции): Если вторая производная дифференцируемой функции положительна (отрицательна) на некотором промежутке Х, то функция выпукла вниз(вверх) на этом промежутке

Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, из которых функция выпукла вверх и вниз .

Точка перегиба- это точка экстремума первой производной.

Теорема 3( необходимое условие перегиба) : Вторая производная дифференцируемой функции в точке перегиба х₀ равна нулю: f’’(x₀)=0

Теорема 4 (достаточное условие перегиба): Если вторая производная дифференцируемой функции в точке х₀ меняет свой знак то х₀ – точка перегиба её графика

Схема исследования функции на выпуклость и точки перегиба:

1. Найти вторую производную функции.

2. Найти точки, в которых вторая производная функции равна нулю или не существует.

3. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и точках перегиба.

4. Найти значения функции в точках перегиба.

57. Асимптоты графика функции (вертикальные, горизонтальные, наклонные)

Асимптотой графика функции y=f(x) называется прямая, такая что расстояние от точки (x,f(x)) до этой прямой стремится к нулю при неограниченном удалении точек графика от начала координат. (НАРИСОВАТЬ ГРАФИКИ)

Теорема 1: Пусть функция y=f(X) определена в некоторой окрестности точки х0 (исключая, может быть, саму эту точку) и хотя бы один из пределов функции при

х→х0 -0 (слева)

или

х→х0+0 (справа)

равен бесконечности , т.е.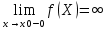



Или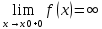



Тогда прямая х=х0 является вертикальной асимптотой графика функции y=f(x)

Вертикальные асимптоты х=х₀ следует искать в точках разрыва функции y=f(X) или на концах её области определения (a,b), если a и b- конечные числа

Теорема 2: Пусть функция y=f(X) определена при достаточно больших х и существует конечный предел функции 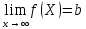. Тогда прямая y=b является горизонтальной асимптотой графика функции y=f(X)

Теорема 3: Пусть функция y=f(X) определена при достаточно больших х и существуют конечные пределы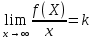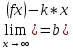



Тогда прямая y=kx+b является наклонной асимптотой графика функции y=f(X)

58. Общая схема исследования функции и построения графика.

1. Найти область определения функции

2. Исследовать функцию на чётность и периодичность

3. Найти вертикальные асимптоты

4. Исследовать поведение функции на бесконечности и найти горизонтальные или наклонные асимптоты

5. Найти экстремумы и интервалы монотонности функции

6. Найти интервалы выпуклости функции и точки перегиба

7. Найти точки пересечения графика с осями координат и некоторые дополнительные точки, уточняющие график.

59. Дифференциал функции, его геометрический смысл .

Дифференциалом функции называется главная, линейная относительно ∆х, часть приращения функции, равная произведению производной на приращение независимой переменной:

d_y= f’(x)*∆x

Геометрический смысл: Дифференциал функции есть приращение ординаты касательной, проведённой к графику функции y=f(X) в данной точке, когда х получает приращение ∆х

Свойства:

1. Дифференциал постоянной величины равен 0: dC=0 (C=const)

2. Постоянный множитель можно выносить за знак дифференциала: d(C*u)=C*du

3. Дифференциал алгебраической суммы ( разности) конечного числа дифференцируемых функций равен сумме ( разности) дифференциалов этих функций: d(u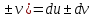

4. Дифференциал произведения двух функций равен сумме произведений дифференциала первого сомножителя на второй и дифференциала второго сомножителя на первый: d(u*v)=du*v+dv*u

5. Дифференциал частного двух дифференцируемых функций находится по формуле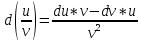

6. Форма дифференциала не меняется, если вместо функции независимой переменной рассматривать функцию от зависимой переменной.

60. Применение дифференциала в приближенных вычислениях.

Приращение функции отличается от дифференциала на бесконечно малую величину: ∆y=dy+a(∆x)*∆x

Поэтому при достаточно малых ∆х:

∆у 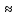dy или

Для приближённых вычислений используется формула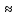: f(x+∆x) f(X)+f’(x)*∆x