Пнрррм. теория ВышМат. 1. Понятие матрицы. Виды матрицы. Матрица
 Скачать 105.27 Kb. Скачать 105.27 Kb.
|
|
28. Деление отрезка в заданном отношении. Если известны две точки плоскости А(Ха;Уа), В(Хв;Ув), то координаты точки М(Хм;Ум), которая делит отрезок АВ в отношении λ= 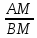 , выражаются формулами: Хм= , выражаются формулами: Хм=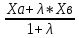 ; Ум= ; Ум=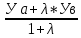 Формулы координат середины отрезка Если даны концы отрезка А(Ха;Уа;Zа), В(Хв;Ув;Zв), то координаты его середины М выражаются формулами: Хм= 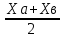 ; Ум= ; Ум=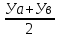 ; Zм= ; Zм=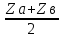 29. Расстояние от точки до прямой. Нормальное уравнение прямой. Под расстоянием от точки М до прямой понимается длина перпендикуляра d, опущенного из точки М на данную прямую. Расстояние от точки до прямой:d= 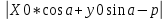 или с учётом вида нормирующего множителя μ(множитель, после умножения на который общее уравнение приобретает вид нормального уравнения) : d= или с учётом вида нормирующего множителя μ(множитель, после умножения на который общее уравнение приобретает вид нормального уравнения) : d=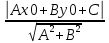 Нормальное уравнение прямой: x*cos a+ ysin a-p=0 Для него характерно: 1)сумма квадратов коэффициентов при переменных х и у равна 1 2)свободный член (-р) – отрицателен. 30. Кривые второго порядка на плоскости. Окружность, эллипс, гипербола, парабола. Окружность и эллипс относятся к кривым второго порядка, которые описываются уравнениями второй степени с двумя переменными. Нормальное уравнение окружности: (Х-Х0)2+(У-У0)2=R2 Если центр окружности лежит в начале координат (0;0): Х2+У2=R2-коаническое уравнение окружности. Эллипсом называется множество точек, сумма расстояний от каждой до двух данных точек, называемых фокусами, есть величина постоянная. Введём обозначения: F1(c;0) F2(-c;0) 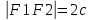 , где , гдеа- большая полуось эллипса b- малая полуось эллипса Для любой точки М(х;у), принадлежащей эллипсу, по определению выполняется равенство: 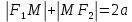 Теорема: Для того, чтобы точка М(х;у) принадлежала эллипсу, необходимо и достаточно, чтобы её координаты удовлетворяли уравнению 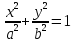 (каноническое уравнение эллипса)где (каноническое уравнение эллипса)где 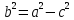 Отношение фокусного расстояния к длине большой оси эллипса называется эксцентриситетом: 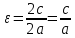 0< 0<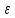 <1 <1 Чем меньше отношение малой и большой полуосей, тем больше эксцентриситет и тем более вытянутым будет эллипс вдоль оси х, и наоборот. При b=a – 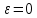 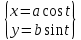 - параметрическое уравнение эллипса - параметрическое уравнение эллипсаГипербола Геперболой называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная( меньшая, чем расстояние между фокусами). F1(c;0) F2(-c;0) 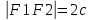 , где , гдеа- действительная полуось гиперболы b- мнимая полуось гиперболы Для любой точки М(х;у), принадлежащей гиперболе, по определению выполняется равенство: 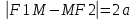 Прямые, проходящие через начало координат и имеющие угловые коэффициенты: 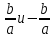 называются асимптотами гиперболы. называются асимптотами гиперболы. Асимптоты делят плоскость на 4 области, в двух из которых расположена гипербола. Точки гиперболы по мере удаления от оси у приближаются к асимптотам, т.е. расстояние между точками гиперболы и асимптотой при увеличении х уменьшается и стремится к нулю. Теорема: Для того, чтобы точка М(х;у) принадлежала гиперболе, необходимо и достаточно, чтобы её координаты удовлетворяли уравнению: 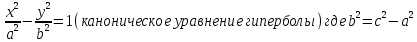 Отношение фокусного расстояния к длине действительной оси гиперболы называется Эксцентриситетом. 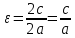 Для гиперболы с˃а --- 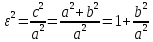 Следовательно, для гиперболы 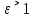 Чем меньше отношение мнимой и действительной полуосей, тем меньше эксцентриситет и тем более гипербола будет прижата к оси х, и наоборот. Парабола. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом параболы и данной прямой, называемой директрисой. Введём обозначения F=( 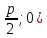 Расстояние между фокусом и директрисой параболы равно р. Для любой точки М(х;у), принадлежащей параболе, по определению выполняется равенство: 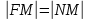 Теорема. Для того, чтобы точка М(х;у) принадлежала параболе, необходимо и достаточно, чтобы её координаты удовлетворяли уравнению у2=2рх(каноническое уравнение параболы) Уравнение директрисы параболы имеет вид: 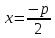 Расстояние 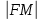 называется фокальным радиусом точки М, р называется параметром параболы. называется фокальным радиусом точки М, р называется параметром параболы.В зависимости от значения этих параметров, возможны различные способы ориентации параболы на плоскости. НАРИСОВАТЬ РИСУНОК!!! 31. Плоскость в пространстве, угол между плоскостями. Общее уравнение плоскости. Общее уравнение плоскости. Пусть плоскость р проходит через точку М(х0,у0,z0) перпендикулярно вектору n(A,B,C). Вектор n называют нормальным вектором плоскости. Возьмём в плоскости Р произвольную точку M(x,y,z). Тогда вектор М0М (х-х0, у-у0,z-z0) будет перпендикулярно вектору n. Следовательно, их скалярное произведение равно 0. Таким образом, 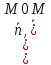 - векторное уравнение плоскости. - векторное уравнение плоскости. Это равенство в координатной форме имеет вид А(х-х0)+В(у-у0)+С(z-z0)=0 – уравнение плоскости, проходящей через заданную точку и перпендикулярной заданному вектору. После преобразования уравнение имеет вид Ах+Ву+Сz+D=0 – общее уравнение плоскости Угол между плоскостями. Условия перпендикулярности и параллельности плоскостей. Пусть заданы дву плоскости Аix+Biy+Ciz+Di=0, i=1. Будем называть углом ф между плоскостями угол образованный нормальными векторами этих плоскостей ni=(Ai,Bi,Ci), i=1,2. Следовательно, 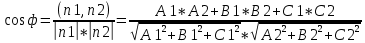 Если плоскости перпендикулярны, то векторы n1 и n2- ортогональны—их скалярное произведение равно нулю, т.е. А1*А2+В1*В2+С1*С2=0 – условие перпендикулярности плоскостей. Если плоскости параллельны, то векторы n1 и n2 – коллинеарны. Следовательно, их координаты пропорциональны 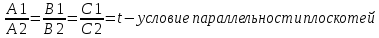 X*cos a+y*cos b+z*cos y-p=0 – нормальное уравнение плоскости d= 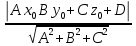 – расстояние от точки до плоскости – расстояние от точки до плоскости 32. Прямая в пространстве. Параметрические уравнения прямой. Канонические уравнения прямой. Угол между прямыми в пространстве. Параметрическое уравнение прямой. Х=х0+t*l, y=y0+tm , z=z0+tn , -∞ Каноническое уравнение прямой: 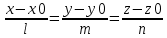 (=t) (=t)Угол между прямыми. Условия параллельности и перпендикулярности прямых. Углом между прямыми l1 и l2 назовём любой угол из двух углов, образованными двумя прямыми, соответственно параллельными данной и проходящими через одну точку Cos ф= 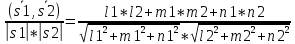 Прямые параллельны, если s1 и s2 коллинеарны – 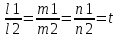 Прямые перпендикулярны – l1*l2+m1*m2+n1*n2=0 Углом между прямой L и плоскостью р называется острый угол между прямой L и её проекцией на плоскость. Sin ф= 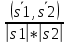 = = 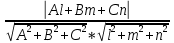 Если прямая параллельна плоскости : Al+Bm+Cn=0 Если прямая перпендикулярна плоскости : 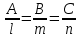 Точка пересечения прямой и плоскости : 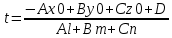 33. Числовые последовательности. Предел числовой последовательности. Если каждому значению n из натурального ряда чисел N(1,2,…) ставится в соответствие по определённому правилу некоторое вещественное число хn , то множество занумерованных вещественных чисел х1,х2…, будем называть числовой последовательностью Отдельные числа х2,х3,х5 будем называть элементами или членами последовательности. Суммой(разностью, произведением, частным) последовательностей (хn) и( yn) называется последовательность (zn), члены которой образованы по правилу zn=xn+yn Произведением последовательности (xn) на число с 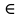 R называется последовательность (с*xn) R называется последовательность (с*xn) Последовательность (xn) называется бесконечно малой, если для любого положительного вещественного числа 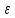 существует номер N, зависящий, вообще говоря от существует номер N, зависящий, вообще говоря от 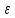 , (N=N( , (N=N(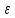 )) такой, что при всех n≥N выполняется неравенство )) такой, что при всех n≥N выполняется неравенство 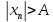 Если последовательность (хn) бесконечно большая и все хn≠0 , то последовательность 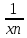 является бесконечно малой , и наоборот является бесконечно малой , и наоборот Свойства бесконечно малых последовательностей: 1. Алгебраическая сумма любого конченого числа бесконечно малых последовательностей есть бесконечно малая последовательность. 2. Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность. 3. Всякая бесконечно малая последовательность является ограниченной. 4. Произведение конечного числа бесконечно малых последовательностей есть бескон6ечно малая последовательность. Предел последовательности. Число а называется пределом последовательности (Хn), если для любого положительного числа  найдётся такое натуральное число N, что при всех n˃N выполняется неравенство найдётся такое натуральное число N, что при всех n˃N выполняется неравенство   34. Понятие функции. Способы задания функций. Сложная функция. Обратная функция. Элементарные функции. Если каждому элементу х множества Х ставится в соответствие определённый элемент у множества У, то говорят, что на множестве Х задана функция у=f(x), где х- называется независимой переменной у- называется зависимой переменной Х- область определения функции У- область значений функции Совокупность точек плоскости ХОУ, удовлетворяющих уравнению y=f(x) называется графиком этой функции. Способы задания функций 1. Аналитический Функция задана формулой вида y=f(x) 2. Табличный Функция задана таблицей, в которой содержатся значения аргумента х и соответствующие значения функции f(x) 3. Графический Функция задана в виде графика y=f(x) Функция х=ф(у) определённая на множестве У с областью значений Х, называется обратной к функции у=f(x) Обратную функцию обозначают у=ф(х)= f-1(x) Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов. Функция у=f  определённая на множестве Х с областью значений У, называется сложной функцией. определённая на множестве Х с областью значений У, называется сложной функцией.Функции, которые можно получить при помощи конечного числа арифметических операций над простейшими элементарными функциями образуют класс элементарных функций. Простейшими элементарными функциями являются: 1. Постоянная у=const 2. Степенная у=xn 3. Показательная у=ах , где а˃0, а≠1 4. Логарифмическая: 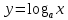 5. Тригонометрическая y=sin x Y=cos x Y= tg x Y= ctg x 6. Обратные тригонометрические: y= arcsin x Y= arcos x Y= arctg x Y= arcctg x В свою очередь, элементарные функции классифицируются следующим образом: 1. Функция вида: Р(х)=a0xn+a1xn-1+…+an-1x+an ,где n≥0-целое число, а0, а1,..аn- любые числа называется целой рациональной функцией 2. Функция представляющая собой отношение двух рациональных функций R(x)= 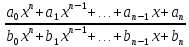 называется дробно-рациональной функцией называется дробно-рациональной функцией3. Функция, в составе которой есть операция извлечения из корня называется иррациональной функцией 4. Функции, которые не являются ни рациональными. Ни рациональными называются трансцендентными 35. Предел функции. Односторонние пределы. Число А называется пределом функции y=f(x), при х 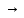 ∞, если для любого, сколь угодно малого числа ∞, если для любого, сколь угодно малого числа 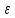 ˃0, найдётся такое положительное число S, что при всех ˃0, найдётся такое положительное число S, что при всех  ˃S , выполняется неравенство: ˃S , выполняется неравенство:   Замечание 1 Рассмотренное определение предела при х стремящимся к бесконечности предполагает неограниченное возрастание х по абсолютной величине. Можно сформулировать понятие предела при стремлении х к бесконечности любого знака, т.е. при Х  должно выполняться при всех х , таких, что х˃s должно выполняться при всех х , таких, что х˃sx 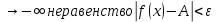 должно выполняться при всех х таких, что х должно выполняться при всех х таких, что хчисло А называется пределом функции у=f(x), при х 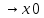 , (или в точке х0) если для любого, сколь угодно малого числа , (или в точке х0) если для любого, сколь угодно малого числа 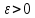 , найдётся такое положительное число , найдётся такое положительное число 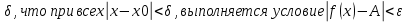  Замечание 2. Определение предела не требует существования функции в самой точке Х0, т.к. рассматриваются значения функции в некоторой окрестности точки Х0. Т.е. рассматривая предел  мы предполагаем, что х мы предполагаем, что х х0, но не достигает значения х0. х0, но не достигает значения х0.Замечание 3. Если при х  переменная х принимает значения только меньше х0 или, наоборот, больше х0, и при этом функция f(x) стремится к некоторому числу А, то говорят об односторонних пределах соответственно справа и слева: переменная х принимает значения только меньше х0 или, наоборот, больше х0, и при этом функция f(x) стремится к некоторому числу А, то говорят об односторонних пределах соответственно справа и слева: 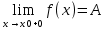 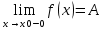 Если пределы функции f(x) слева и справа одинаковы и равны А, то существует общий предел этой функции, также равный А: 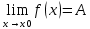 |
