1. Сформулируйте понятия оптимизация и оптимальное решение
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
|
1. Сформулируйте понятия: оптимизация и оптимальное решение. Оптимизация – это процесс поиска наилучшего решения из некоторого множества допустимых решений. Оптимальное решение – это наилучшее решение из некоторого множества допустимых решений. 2. Что такое математическая формализация задачи? Математическая формализация задачи - способ выражения содержания совокупности условий через определенную форму- знаки искусственного языка. 3. Перечислите основные критерии оптимизации, применяемые в задачах энергетики. В электроэнергетике в зависимости от требований поставленной задачи могут приниматься и другие критерии оптимальности, в частности: - критерий надежности электроснабжения; - критерий качества электроэнергии; - критерий наименьшего отрицательного воздействия на окружающую среду (экологический критерий). 4. Дайте понятие линейной и нелинейной зависимостей между переменными. Линейной называется такая зависимость, в которую переменные xi (i=1, 2, 3, … n) входят только в первой степени и с этими переменными выполняются только действия сложения, вычитания и умножения на постоянный коэффициент. Во всех других случаях зависимость будет нелинейной. 5. Определите основные понятия математической модели: целевая функция, ограничения, граничные условия. Формализованное математическое описание оптимизационной задачи, другими словами, математическая модель включает в себя: - целевую функцию; - ограничения; - граничные условия. Целевая функция представляет собой математическую запись критерия оптимальности. Ограничения представляют собой различные технические, экономические, экологические условия, учитываемые при решении задачи. Ограничения представляют собой зависимости между переменными х1, х2, ... хn, задаваемые в форме неравенств или равенств f1(х1, х2, ... хn) < b1; f2(х1, х2, ... хn) = b2; (1.2) . . . . . . . . . . . . . . . . . . . fm(х1, х2, ... хn) > bm. Общее количество ограничений равно m. Правые части ограничений, представляющие собой постоянные коэффициенты bj (j=1, 2, … m), называются свободными членами. Граничные условия устанавливают диапазон изменения искомых переменных
где di и Di - соответственно нижняя и верхняя границы диапазона изменения переменной xi. Наиболее часто в технических задачах все искомые переменные, как правило, неотрицательны. В этом случае граничные условия имеют следующий вид: хi > 0, где i = 1, 2, ... n. 6. Запишите линейную математическую модель оптимизационной задачи. Линейная математическая модель в общем случае имеет следующий вид: Z = z1x1+z2x2+...+znxn → extr, a11x1+a12x2+...+a1nxn < b1, a21x1+a22x2+...+a2nxn = b2, . . . . . . . . . . . . . . . . . . . . . . . . am1x1+am2x2+...+amnxn > bm, хi > 0, i = 1, 2, ... n, где zi, bj, aji - заданные постоянные величины, i = 1.2,…n; j = 1, 2, ... m. 7. Назовите основные методы решения линейных оптимизационных задач и основные этапы этих методов. 1) Графический метод является достаточно простым, наглядным и позволяет сделать некоторые общие выводы по решению оптимизационных задач методами линейного программирования. Однако применение графического метода ограничено задачами относительно небольшой размерности. 2) Алгебраический метод 3) Симплекс-метод является универсальным аналитическим методом решения задач линейного программирования. Идея симплекс-метода заключается в последовательном переборе решений – в последовательном переходе от одной вершины к другой. Однако этот перебор не хаотичный, а таков, что на каждом шаге решение улучшается. Метод состоит из двух этапов: на первом этапе ищется допустимое решение допустимое решение; на втором этапе это допустимое решение улучшается до оптимального. 1 этап. Получение допустимого решения. Любое допустимое решение должно удовлетворять системе ограничений-равенств и граничным условиям. 2 этап. Получение оптимального решения. Пусть оптимальному решению соответствует минимальное значение целевой функции Z. Необходимо проверить возможность улучшения полученного на первом этапе допустимого решения, то есть проверить возможность уменьшения значения целевой функции Z. 8. Дайте графическую иллюстрацию целевой функции, ограничения и граничного условия в задаче линейного программирования Целевой функция Z = z1x1+z2x2 → min, при ограничениях a11x1+a12x2 < b1, a21x1+a22x2 < b2, a31x1+a32x2 < b3, и граничных условиях неотрицательности переменных хi > 0, i = 1, 2.  9. Что представляет собой область допустимых решений в задаче линейного программирования? 
плоскости х1х2 выделится область Ω допустимых значений переменных х1, х2, х3, х4, х5 (рис). Эта область представляет собой выпуклый многогранник abcde. Все допустимые решения задачи, в том числе и оптимальное решение, будут принадлежать области Ω. Оптимальное решение задачи всегда находится в одной из вершин многогранника Ω, поэтому для отыскания оптимального решения достаточно рассмотреть только конечное количество решений, лежащих в вершинах многогранника Ω, и не рассматривать бесконечное количество решений, лежащих на гранях и внутри этого многогранника; 10.Определите понятия: базисная и свободная переменная Базисная переменная - это такая неизвестная переменная, для которой столбцы матрицы системы, соответствующие этим неизвестным, образуют матрицу, ранг которой равен рангу всей матрицы системы вместе со столбцом свободных членов. Свободные переменные - это остальные переменные, не являющиеся базисными 11. Опишите процедуру алгебраических преобразований системы линейных уравнений. Суть процедуры заключается в следующем: из первого уравнения системы выражается переменная x1 и подставляется во второе и третье уравнения системы. В результате такого преобразования свободная переменная х1 становится базисной, а базисная переменная x3 становится свободной. 1. Все коэффициенты, не принадлежащие разрешающей строке и разрешающему столбцу, пересчитываются по выражению где aij - коэффициент, лежащий на пересечении i-й строки и j-го столбца; aij'- новое пересчитанное значение коэффициента aij, arr - разрешающий коэффициент; air - коэффициент, лежащий на пересечении i-й строки и разрешающего столбца; arj - коэффициент, лежащим на пересечении разрешающем строки и j-го столбца. 2. Все коэффициенты разрешающей строки делятся на разрешающим коэффициент arr. Разрешающий коэффициент при этом становится равным единице arr=1. 3. Все коэффициенты разрешающего столбца, кроме разрешающего коэффициента, заменяются нулями. 12. Как осуществляется выбор разрешающего столбца и разрешающей строки при поиске допустимого решения симплекс-методом? Если среди свободных членов есть отрицательные, то выбирается любой из них и соответствующая строка принимается в качестве разрешающей. Базисная переменная, отвечающая разрешающей строке, будет переводиться в разряд свободных. 13. Как осуществляется выбор разрешающего столбца и разрешающей строки при поиске оптимального решения симплекс-методом? Следовательно, условием получения оптимального решения при минимизации целевой функции является неотрицательность коэффициентов целевой функции zi'>0. Если среди коэффициентов целевой функции есть отрицательные, то берется любой из них и соответствующий этому коэффициенту столбец принимается в качестве разрешающего. Свободная переменная, отвечающая разрешающему столбцу, будет переводиться в базис. 14. Сформулируйте условие допустимого решения в симплекс-методе. Следовательно, условием получения допустимого решения является неотрицательность свободных членов ограничений равенств. 15. Сформулируйте условие оптимального решения в симплекс-методе. Следовательно, условием получения оптимального решения при минимизации целевой функции является неотрицательность коэффициентов целевой функции zi'>0. 16. Дайте формулировку транспортной задачи. Транспортная задача - это задача отыскания таких путей перевозки продукта от пунктов производства к пунктам потребления, при которых общая стоимость перевозок оказывается минимальной. 17. Запишите математическую модель транспортной задачи. Затраты на электрическую сеть равны сумме произведений удельных стоимостей на величины передаваемых мощностей от источников i к потребителям j. Поэтому подлежащая минимизации целевая функция имеет следующий вид:
С позиций теоретической электротехники электрическая сеть является электрической цепью и для этой сети применимы все законы, известные из курса электротехники, в частности 1-й закон Кирхгофа. Для каждого i-го источника питания сумма мощностей, оттекающих по линиям ко всем j=1,2,...m узлам потребителей, равна мощности Ai этого источника m 31
j=1 \(\sum_{j=1}^{m} x_ij=A_i\) Для каждого j-го потребителя сумма мощностей, притекающих по линиям от всех i=1,2,...n источников, равна мощности Bj этого потребителя
В рассматриваемой постановке транспортной задачи все искомые мощности хij, передаваемые от источников к потребителям, являются неотрицательными. Следовательно, граничные условия имеют вид
линейными. Следовательно, транспортная задача может быть решена симплекс-методом. 18. Каковы особенности ограничений в транспортной задаче. Соотношения (3.2) и (3.2а), представляющие собой балансы мощности в каждом из узлов, являются ограничениями при решении транспортной задачи. Общее количество ограничений равно количеству узлов источников и потребителей n+ m. все ограничения имеют форму равенств; 19. Сформулируйте принцип отыскания допустимого решения в транспортной задаче. Исходное допустимое решение может быть получено по алгоритму минимальной удельной стоимости: 1.В транспортной матрице выбирается клетка с минимальным значением zij. Если имеется несколько таких клеток, то выбирается любая из них. 2.В выбранную клетку в качестве базисной переменной заносится наименьшая из двух величин Ai или Bj, т.е. xij=min(Ai,Bj). При этом выполняется баланс мощности по строке i или столбцу j, в которые входит переменная xij. 3.В остальные клетки строки i или столбца j, для которых выполнен баланс мощности, заносятся нули, соответствующие свободным переменным. Большая из двух величин Ai и Bj условно заменяется разностью этих двух величин. 4.Из оставшихся незаполненных клеток транспортной матрицы вновь выбирается клетка с минимальным значением zij. Далее пункты 2 и 3 повторяются до полного заполнения всех клеток транспортной матрицы. Следует напомнить, что общее количество переменных составляет nm. Количество отличных от нуля базисных переменных составляет (n+m-1). Количество равных нулю свободных переменных составляет (nm-(n+m-1)). 20. Каково условие допустимого решения в транспортной задаче? Исходное допустимое решение может быть получено по алгоритму минимальной удельной стоимости: Вся транспортная матрица заполнена. Балансы мощности по строкам (по узлам источников) и по столбцам (по узлам потребителей) выполняются. Все переменные неотрицательны. Полученное исходное решение является допустимым. 21. Каково оптимальное решение транспортной задаче. Изменение целевой функции при увеличении на единицу свободной переменной х21 составит
Если для каждой свободной переменной изменение целевой функции ∆Z>0, то полученное решение будет оптимальным. 22. Поясните понятие транзита мощности через узел. Транзит мощности через узел – передача мощности через промежуточный узел, без потребление в этом узле. Такими транзитными узлами могут быть как узлы источников питания, так и узлы потребителей. Таким образом, транспортная задача с транзитом мощности является более общей задачей и имеет более широкие возможности по оптимизации схемы электрической сети, чем транспортная задача в классической постановке. 23. Какова стоимость передачи транзитной мощности через узел. Удельные затраты на передачу транзитной мощности через любой i-й узел zii=0. Целевая функция представляет собой сумму произведений удельных стоимостей на величины передаваемых мощностей от узла i к узлу j  \(Z=\sum_{i=1}^{n+m} \sum_{j=1}^{n+m} z_{ij}x_{ij} \to min, i\neq j\)  \(\sum_{j=1, i≠j}^{n+m} x_{ij}-x_{ii}=A_i\) 24. Что такое цикл пересчета транспортной матрицы. В новом решении строятся циклы пересчета и определяются изменения целевой функции ∆Z для каждой свободной переменной х12 и х23. Если для каждой свободной переменной изменение целевой функции ∆Z>0, то полученное решение будет оптимальным. 6. Если имеются свободные переменные, для которых Vi+Uj>zij, то выбирается любая из этих свободных переменных и переводится в базис. Для этого строится цикл пересчета (замкнутая ломаная линия), начальная вершина которого лежит в клетке выбранной свободной переменной. Остальные вершины цикла лежат в клетках, соответствующих базисным переменным. Начальной вершине цикла присваивается знак "+", соответствующий увеличению переменной. Далее знаки вершин цикла чередуются. Знаки "+" соответствуют увеличению базисных переменных, знаки "-" – их уменьшению. 7.Из отрицательных вершин цикла выбирается вершина с наименьшим значением базисной переменной и на эту величину изменяются все переменные, лежащие в вершинах цикла. В положительных вершинах переменные увеличиваются, в отрицательных - уменьшаются. При этом выбранная свободная переменная становится базисной, а наименьшая по величине базисная переменная в отрицательной вершине цикла становится свободной (равной нулю). 25. Приведите примеры задач энергетики, решаемых методами линейного программирования.  Выбор оптимальной конфигурации электрической сети (транспортная задача) Определение оптимального количества трансформаторов цеховых подстанций. Задача с прибылью от реализации изделий и нормами расхода электроэнергии. 26. Запишите в общем виде математическую модель задачи нелинейного программирования. целевая функция: Z(x1, x2, ... xn) → extr n переменных, при m ограничениях, заданных в форме равенств и (или) неравенств f1(x1, x2, ... xn)= b1, f2(x1, x2, ... xn)> b2, . . . . . . . . . . . . . . . . .. fm(x1, x2, ... xn)< bm, граничных условиях di < хi < Di, i = 0, 1, 2, ... n. Если в математической модели оптимизационной задачи имеются нелинейные зависимости, для решения этой задачи используются методы нелинейного программирования. 27. Назовите основные методы решения нелинейных оптимизационных задач. 1. Градиентные методы       28. Дайте графическую иллюстрацию целевой функции в задаче нелинейного программирования. Графическую иллюстрацию нелинейной оптимизационной задачи рассмотрим для случая двух переменных х1 и х2. Пусть нелинейная целевая функция Z(х1,х2) имеет вид, показанный на рис. 4.1.  представление линиями равного уровня Z = const Пересечем функцию Z плоскостями, параллельными горизонтальной плоскости х1,х2. Точки пересечения спроектируем на плоскость х1,х2. На плоскости х1,х2 получим замкнутые концентрические кривые. На каждой из этих замкнутых кривых значение целевой функции неизменно
29. Дайте графическую иллюстрацию ограничений в задаче нелинейного программирования. Ограничения (4.2) могут быть линейными и нелинейными, заданными в виде неравенств или равенств. Как было показано при рассмотрении задач линейного программирования, линейные ограничения представляют собой прямые линии. Очевидно, что нелинейные ограничения будут представлять собой кривые линии. При ограничениях-равенствах допустимые значения переменных принадлежат прямой (кривой) линии, при ограничениях-неравенствах допустимые значения переменных принадлежат полупространству, расположенному по одну сторону от прямой (кривой) линии. На рис. 4.2 показан случай, когда два ограничения 1 и 2 являются линейными неравенствами, а одно ограничение 3 - нелинейным неравенством. Штриховка у каждого ограничения направлена в сторону допустимых значений переменных.  Рис. 4.2. Иллюстрация области Ω допустимых значений переменных и относительного минимума функции Z 30. Дайте понятие линий равного уровня целевой функции. Пересечем функцию Z плоскостями, параллельными горизонтальной плоскости х1,х2. Точки пересечения спроектируем на плоскость х1,х2. На плоскости х1,х2 получим замкнутые концентрические кривые. На каждой из этих замкнутых кривых значение целевой функции неизменно
Полученные замкнутые кривые Z = const называются линиями равного уровня целевой функции Z. Напомним, что для линейной задачи линии равного уровня Z=const представляли собой прямые линии (рис. 2.2). Линии равного уровня целевой функции – кривые, значение целевой функции на которых неизменно. Для линейной задачи – прямые, Для нелинейной – замкнутые кривые. 31. Сформулируйте понятие градиента целевой функции. Пояснить физический смысл градиента. Градиент целевой функции – это вектор  (1), (1), где \(gradZ=\frac{∂Z}{ { ∂x }_{ 1 } }\overline{i}+\frac{∂Z}{ { ∂x }_{ 2 } }\overline{j}+...+\frac{∂Z}{ { ∂x }_{ n } }\overline{k}\) Величина градиента определяется по выражению \(|gradZ|=\sqrt { { (∂Z/∂x_1) }^{ 2 } + { (∂Z/∂x_2) }^{ 2 } +...+ { (∂Z/∂x_n) }^{ 2 } } \) Из формул (1) и (2) видно, что функция, градиент которой определяется, должна быть дифференцируемой по всем n переменным. Физический смысл – градиент показывает направление (1) и скорость (2) наибольшего изменения функции в рассматриваемой точке. Если в некоторой точке |grad Z|=0, функция в этой точке не изменяется (не возрастает и не убывает). Эта точка соответствует экстремуму функции. 32. Поясните суть градиентных методов решения нелинейных задач. Эти методы решения нелинейных задач используют понятие градиента функции. В области допустимых значений переменных целевой функции выбирается исходное (нулевое) приближение – точка с координатами x10 и x20, значение целевой функции в которой составляет Z0. В этой точке вычисляется градиент функции, затем выполняется шаг в направлении убывания функции (например, λ=1). В результате выполненного шага получается первое приближение – точка с координатами x11 и x21, значение целевой функции в которой составляет Z1. Далее процедура повторяется, пока относительное изменение целевой функции на предыдущем i-ом и последующем i+1 шагах оказывается меньше заданной точности вычислений ε (Zi – Zi+1)/Zi≤ε Для получения более точного результата необходимо выбирать шаг меньшей длины, но при этом увеличивается количество шагов вычислений. 33. Поясните понятия: безусловный и условный экстремумы нелинейной функции. Безусловный экстремум нелинейной функции – абсолютный экстремум целевой функции, поиск которого осуществляется без ограничений и граничных условий. Условный экстремум нелинейной функции - относительный экстремум целевой функции, поиск которого осуществляется с ограничениями и граничными условиями. Методы решения безусловных экстремумов являются основой поиска условных экстремумов нелинейной функции. 34. Как ищется безусловный экстремум нелинейной функции? Поиск осуществляется без ограничений и граничных условий. Для нахождения n переменных определяются частные производные нелинейной функции по всем переменным и приравниваются к нулю. Полученную систему n уравнений с n неизвестными решают, получают значения переменных, при которых достигается экстремум функции. 35. Поясните суть метода неопределенных множителей Лагранжа. Метод Лагранжа – процедура сведения задачи условной оптимизации к более простой задаче безусловной оптимизации. Если требуется найти условный экстремум нелинейной функции с n переменными и m ограничениях, то ограничения-неравенства преобразуются в равенства, а свободные члены переносятся в левые части ограничений. При этом вместо относительного (условного) экстремума функции при заданных ограничениях ищется абсолютный (безусловный) экстремум функции Лагранжа, которая имеет вид  (1), (1),L=Z(x1, x2, …, xn)+ λ1f1(x1, x2, …, xn, b1)+ λ2f2(x1, x2, …, xn, b2)+… λmfm(x1, x2, …, xn, bm)→extr где λ1, λ2, …, λm - неопределенные множители Лагранжа, являющиеся искомыми переменными, как и переменные x1, x2, …, xn. Как видно в функцию Лагранжа входит целевая функция плюс каждое ограничение, умноженное на множитель Лагранжа. Поиск абсолютного (безусловного) экстремума функции Лагранжа выполняется следующим образом: определяются и приравниваются к нулю частные производные функции Лагранжа, полученную систему решают либо методом Гаусса, если система линейная, либо методом Ньютона, если система нелинейная. При этом система имеет m+n уравнений и такое же количество неизвестных. Решение системы дает координаты абсолютного (безусловного) минимума функции Лагранжа или относительного (условного) минимума целевой функции при заданных ограничениях. 36. Приведите примеры задач энергетики, решаемых методами нелинейного программирования. Задачи оптимального распределения активной мощности в энергосистеме, задачи оптимального распределения компенсирующих устройств в системах электроснабжения. Этим методом решаются оптимизационные задачи, если в математической модели имеются нелинейные зависимости между переменными. 37. Приведите примеры задач энергетики, решаемых методами целочисленного и дискретного программирования. Целочисленное программирование: определение максимальной прибыли предприятия. Двоичные переменные: выбор оптимального варианта из определенного числа заданных вариантов (выбор линии электропередачи). Дискретное программирование: определение оптимального узла установки компенсирующего устройства заданной мощности в системе электроснабжения. Этими методами решаются оптимизационные задачи, если среди переменных имеются целочисленные или дискретные переменные. 38. Приведите примеры задач энергетики, решаемых методами стохастического программирования. Задача распределения ресурсов, когда количество сырьевого ресурса на предприятии является случайной величиной. 39. Приведите примеры многокритериальных оптимизационных задач. Задача определения оптимального выпуска продукции, обеспечивающего предприятию максимальную прибыль при минимальных расходах энергетических ресурсов. 40. Поясните понятия: целочисленная, двоичная, дискретная переменная. Целочисленная переменная – переменная, которая может принимать только значения целых чисел (количество трансформаторов для электроснабжения объекта или количество изделий, выпускаемых промышленным предприятием). Двоичная переменная – переменная, которая может принимать значение либо 0, либо 1. Дискретная переменная – переменная, которая может принимать только определенные значения (искомая мощность трансформатора или искомое сечение линии электропередачи, значение величин которых регламентируется ГОСТ). 41.Какие переменные обязательно сопровождают решение дискретной задачи? Дискретные задачи представляют собой такие задачи, в которых необходимо произвести выбор вариантов из числа заданных. При решении данных задач используют не только традиционные переменные, но и двоичные переменные δi, где i=1, 2, …, n. Если вариант входит в оптимальное решение, то двоичная переменная, соответствующая этому варианту, равна 1. Если вариант не входит в оптимальное решение, то соответствующая двоичная переменная равна 0. δi+ δj=1 - если в оптимальное решение должен входить один из двух (i и j) вариантов; δi+ δj=2. - если в оптимальное решение должны входить и i–й и j–й варианты; δi+ δj≥0 - если в оптимальное решение может входить или не входить каждый из двух (i и j) вариантов δi= δj - если при входе (не входе) в оптимальное решение i–го варианта в это решение должен войти (не войти) и j–й вариант 42. Из n возможных вариантов в оптимальное решение входит m вариантов. Приведите типичное для такой дискретной задачи ограничение Если при решении дискретной задачи из n возможных вариантов в оптимальное решение должны входить только m вариантов (m < n), то следует указать следующее ограничение: δ1+ δ2+…+ δn=m, где δ1, δ2, δn – двоичные переменные всех n возможных вариантов. 43. Сформулируйте причины и приведите примеры случайной исходной информации. В практических задачах зачастую исходная информация не может быть однозначно определена и имеет случайный характер (может представлять собой случайные величины или функции). При этом случайные величины могут быть непрерывными или дискретными. Приведем некоторые примеры случайной исходной информации: 1) Случайная величина: а) непрерывная: - мощности нагрузок в проектируемой системе электроснабжения (СЭС); - величина напряжения в узле СЭС. б) дискретная: - количество одновременно работающих в энергосистеме генераторов. 2) Случайная функция: - изменение во времени напряжений в узлах существующей СЭС. 44. Каким методом решаются задачи при случайной исходной информации? Для решения оптимизационных задач со случайной исходной информацией используются методы стохастического программирования. Однако универсальных методов решения задач стохастического программирования, пригодных для всех классов оптимизационных задач, не существует. Рассмотрим математическую модель стохастических задач линейного программирования. Математическая модель задачи стохастического программирования имеет следующий вид: - Если коэффициенты целевой функции являются случайными величинами, ищется экстремальное значение математического ожидания целевой функции: М[Z] → extr. - Если коэффициенты aij и (или) bj системы ограничений являются случайными величинами, то для каждого j-го ограничения задается значение вероятности Рзад j, с которой должно выполняться это ограничение. Вероятность выполнения каждого j-го ограничения должна быть не меньше заданной: P(aj1x1+aj2x2+...+ajnxn≤bj)≥ Рзад j, j =1, 2,… m. - Границы диапазона изменения переменных: di ≤хi ≤Di, i = 1, 2, ... n. 45. Каковы математическое ожидание и среднеквадратичное (стандартное) отклонение стандартной случайной величины? Стандартная случайная величина η – это случайная величина, вероятность появления которой в интервале -3≤ η≤3 описывается нормальным стандартным законом распределения. Стандартная случайная величина имеет: - Математическое ожидание, равное М[η]=0; - Среднеквадратичное отклонение σ[η]=1. Математическим ожиданием случайной величины называется ее среднее значение, полученное в результате n реализаций:  где  – значение случайной величины в i-й реализации. – значение случайной величины в i-й реализации.\(M[s]=\frac{1}{n}\sum_{i=1}^{n} { s }_{ i } \) Среднеквадратичное (стандартное) отклонение определяет разброс значений случайной величины относительно ее математического ожидания:  \(σ[s]=\sqrt { \frac{ { \sum_{i=1}^{n} (si-M[s]) }^{ 2 } }{n-1} }\) 46. Запишите выражение, связывающее случайную величину S и стандартную случайную величину η. Случайная величина s – величина, которая может принять то или иное значение, причем заранее неизвестно, какое именно. Может быть непрерывной или дискретной. Стандартный закон распределения – закон, описывающий вероятность появления стандартной случайной величины η с математическим ожиданием М[η]=0 и среднеквадратичным отклонением σ[η]=1 в интервале -3 ≤η ≤3. От функции распределения нормального стандартного закона можно перейти к функции распределения нормального закона любой случайной величины s оптимизационной задачи. Связь между этой случайной величиной s и стандартной случайной величиной η выражается зависимостью: s = М[s] + ησ[s]. 47. Назовите основные стратегии выбора решения в задаче с исходной недетерминированной информацией В реальных оптимизационных задачах часто приходится искать решение в условиях неопределенности, основной причиной которой является недостаток исходной информации. Для решения оптимизационных задач с недетерминированной информацией вместо методов математического программирования используется вычислительный аппарат теории игр. Рассмотрим основные стратегии выбора решения, которые предлагает теория игр: 1. Стратегия минимума средних затрат. В соответствии с этой стратегией для каждого хода xi человека определяются средние затраты по всем возможным ходам системы m:  \( { Z }_{ срi } =\frac{ { \sum_{j=1}^{m} z }_{ i } }{m}\) Выбирается решение, отвечающее минимуму из совокупности i =1, 2, … n средних затрат:  \( { x }_{ i } \to \underset{i=1}\overset{n}{min} { Z }_{ срi } \) При этой стратегии считается, что все ходы системы имеют одинаковую вероятность, равную 1/m. Для реальных задач такое предположение, как правило, не является истиной. 2. Миниминная стратегия. В соответствии с этой стратегией считается, что на каждый ход xi человека система ответит ходом yj, соответствующим минимальным затратам:  \( { z }_{ mini } =\underset{j=1}\overset{m}{min} { z }_{ ij } \) Выбирается решение, отвечающее минимуму из совокупности i =1, 2, … n минимальных затрат:  \( { x }_{ i } \to \underset{i=1}\overset{n}{min}\underset{j=1}\overset{m}{min} { z }_{ ij } \) Принятие решения по этой стратегии может привести к крупным просчетам, поскольку здесь учитывается самая благоприятная ситуация. Систему нельзя считать разумным игроком, однако она не будет играть и в поддавки. 3. Минимаксная стратегия. В соответствии с этой стратегией считается, что на каждый ход xi человека система ответит ходом yj, соответствующим максимальным затратам:  \( { z }_{ maxi } =\underset{j=1}\overset{m}{max} { z }_{ ij } \) Выбирается решение, отвечающее минимуму из совокупности i =1, 2, … n максимальных затрат:  \( { x }_{ i } \to \underset{i=1}\overset{n}{min}\underset{j=1}\overset{m}{max} { z }_{ ij } \) В этой стратегии учитывается самая неблагоприятная ситуация. Считается, что система является разумным игроком и стремится к максимальному выигрышу. Такое предположение не соответствует действительности. 4. Стратегия Гурвица. Эта стратегия учитывает как самую благоприятную, так и самую неблагоприятную ситуации. Здесь решение выбирается по условию:  \( { x }_{ i } \to \underset{i=1}\overset{n}{min}(k\underset{j=1}\overset{m}{max} { z }_{ ij } +(1-k)\underset{j=1}\overset{m}{min} { z }_{ ij } )\) где коэффициенты k и (1-k) играют роль весовых коэффициентов, с которыми учитываются минимаксная и миниминная стратегии. При k=1 имеем минимаксную стратегию, а при k=0 имеем миниминную стратегию. Наибольшую трудность при применении этой стратегии представляет определение величины весовых коэффициентов k и (1-k). Теория игр ответа на этот вопрос не дает. Для каждой конкретной задачи весовые коэффициенты определяются индивидуально, на основе имеющегося опыта. Таким образом, для решения оптимизационной задачи при недетерминированной исходной информации теория игр выдвигает ряд стратегий. Поскольку формально все стратегии равноправны, окончательное решение должно выбираться на основе: - анализа решений, полученных по каждой стратегии; - опыта проектировщика; - особенностей конкретной задачи. 48. Поясните суть метода экспертных оценок. Метод экспертных оценок – это метод определения весовых коэффициентов критериев при решении многокритериальных задач оптимизации. Суть данного метода заключается в следующем. Пусть для решения оптимизационной задачи приняты, например, три критерия (критерий А, критерий В и критерий С). Собирается группа экспертов – специалистов в той области, к которой относится оптимизационная задача. Пусть группа экспертов состоит, например, из трех человек (1-й эксперт, 2-й эксперт и 3-й эксперт). Каждому эксперту предлагается оценить в баллах от 0 до 1 каждый критерий. При этом выдвигается условие, чтобы сумма баллов каждого эксперта по всем критериям была бы равна 1. В таблице представлены результаты экспертизы. В качестве весового коэффициента i-го критерия (i=A, B, C) принимается среднее значение оценок каждого эксперта по этому критерию.
49.Запишите обобщенную целевую функцию многокритериальной задачи. Обобщенная целевая функция многокритериальной задачи записывается следующим образом: 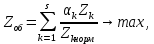 \( { Z }_{ об } =\sum_{k=1}^{s} \frac{ { \alpha }_{ k } { Z }_{ k } }{ { Z }_{ kнорм } } \) где 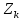 – k-я целевая функция, выражающая k-й критерий; – k-я целевая функция, выражающая k-й критерий; 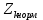 – нормированное значение k-й целевой функции; – нормированное значение k-й целевой функции;  – коэффициент веса k-й целевой функции; s – количество целевых функций (принятых критериев). – коэффициент веса k-й целевой функции; s – количество целевых функций (принятых критериев).Если k-я целевая функция максимизируется, перед ней под знаком суммы ставится плюс. Если k-я целевая функция минимизируется, перед ней под знаком суммы ставится минус. 50.Поясните понятие: нормированное значение целевой функции. Нормированное значение k-й целевой функции Zk норм принимается по результатам решения оптимизационной задачи только по одному k–му критерию. Целевые функции в общем случае имеют разные единицы измерения. Поэтому в формуле для определение обобщенной целевой функции 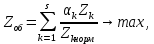 введено деление каждой целевой функции на ее нормированное значение. Такое действие приводит все целевые функций к единой размерности (к относительным единицам, о.е.). \( { Z }_{ об } =\sum_{k=1}^{s} \frac{ { \alpha }_{ k } { Z }_{ k } }{ { Z }_{ kнорм } } \) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
