Прикладная математика. шпоры по прикладной математике. 1. слау основные определения, каноническая форма записи слау
 Скачать 0.72 Mb.
|
|
О  сновной задачей линейного программиро-вания называется задача отыскания min ли-нейной формы z =  cj xj, при неотрицатель-ности входящих в нее переменных и системы ограничений в виде СЛАУ aijxj ≤ bi xj≥ 0; i=  ; j= .
Ф-я z заменяется на “-z”. В левой части сис-мы ограничений СЛАН вводится по одной искусствен-ной переменной в каждое из неравен-ств. Найти план производства xj, j= обеспечивающий min линейной формы - z = - cj xj → min. И ограничения aijxj + x’i = bi xj ≥ 0; x’i≥0, i= ; j= .Исходные параметры задачи могут быть представлены в виде технологической матрицы A затрат ресурсов на единицу продукции каждого вида, вектора B объемов ресурсов и вектора C удельной прибыли: 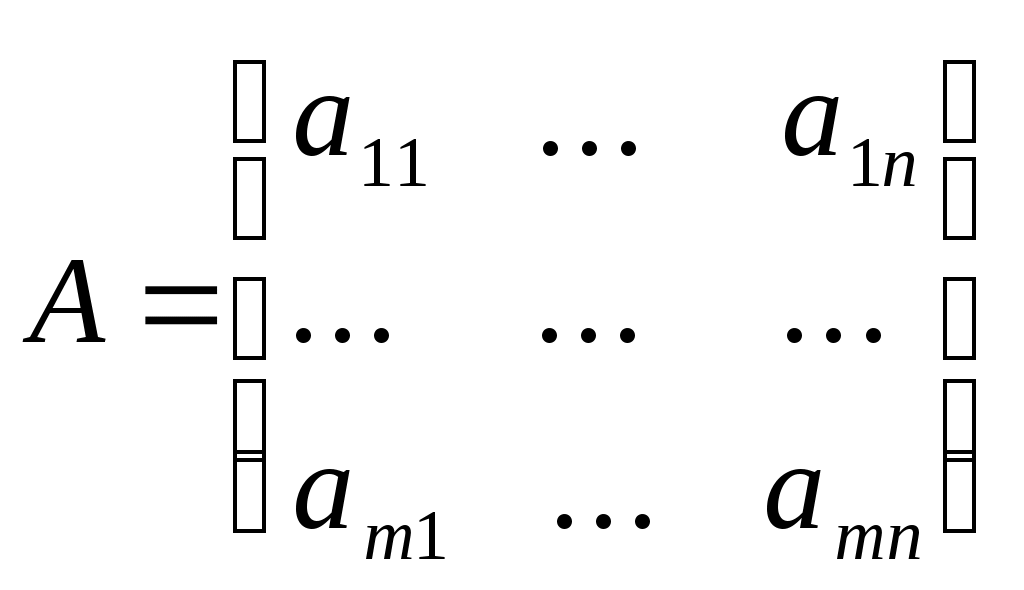  C=(c1, …, cn).Матричная форма записи: 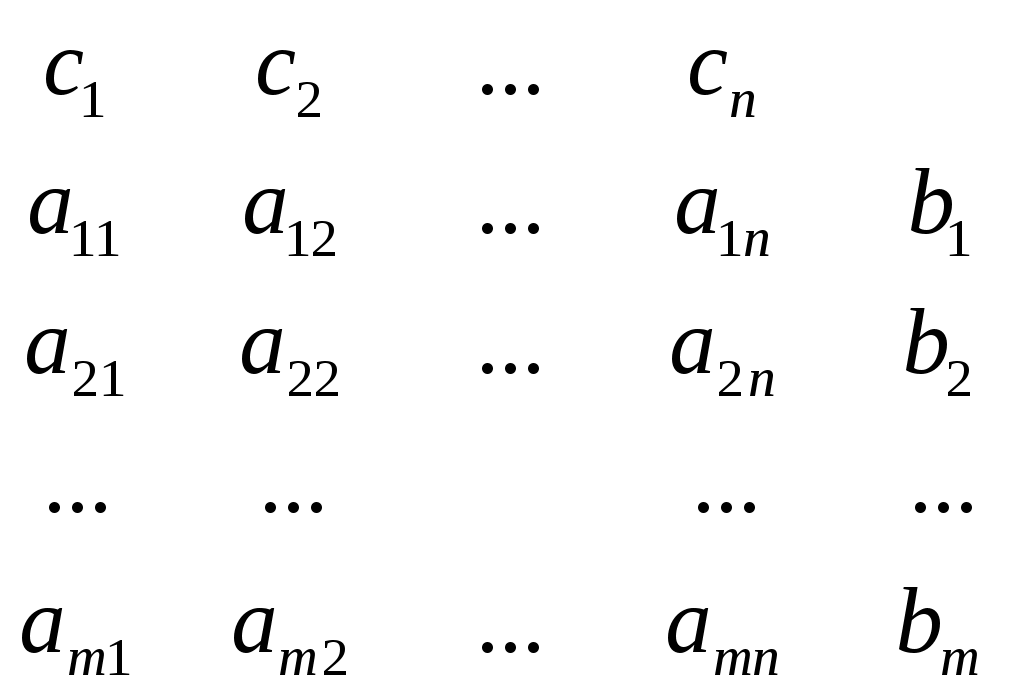 14. Геометрическая интерпретация задачи ЛП и симплексного метода. Графическое решение задачи ЛП с 2мя переменными. 15. Симплексметод ЛП: задача ЛП в предпочитаемой форме, выражение функции цели через свободные неизвестные, вычис-ление относительных оценочных коеффици-ентов ∆jи значение целевой функции соответ-ствующих данному базисному допустимому решению. Рассмотрим частный случай общей задачи, когда система уравнений имеет предпочитаемый вид, при этом правые части всех уравнений неотрицательны. М инимизировать L=c1x1+c2x2+...cnxn (1), при условиях:x1 + g1,m+1xm+1 + ... + g1nxn = h1, x2 + g2,m+1 xm+1 + ... + g2nxn = h2, (2) ... ... ... ... xm + gm,m+1 xm+1 + ... + gmnxn = hm и xj≥0, j = 1,2,...n (3). Одним из допустимых решений задачи линейного программирования (1)-(3) будет базисное неотрицательное решение системы (2): x1=h1, x2=h2,...xm=hm, xm+1=0,...xn=0 (4), ему соответствует значение целевой ф-ии равное L0=c1h1+c2h2+...cmhm+cm+1*0+...+cn*0 =  ci hi (5).Надо исследовать, является ли решение (4) оптимальным (т.е. является ли значение (5) наименьшим из всех возможных значений целевой ф-ии (1), отвечающих различным неотрицательным решениям системы (2)). Учитывая что система уравнений (2) имеет предпочитаемый вид, находим для нее общее решение: xi=hi-gi,m+1xm+1-...-ginxn, i=1,2,...,m (6). Если свободным неизвестным придавать какие-нибудь неотрицательные значения, то будем получать различные решения системы (2), среди которых нас интересуют только неотрицательные. Подставляя их компоненты в линейную форму (1), можно подсчитать соответствующие значения целевой функции. Если переписать выражение (1) в виде: - L = c1x1+c2x2+...cmxm+ cm+1xm+1+...+cnxn=0 (7). Для того чтобы исключить базисные неизвестные из (7) , достаточно умножить первое уравнение системы (2) на c1, второе- на c2, … , m-e на cm, сложить полученные произведения и из результата вычесть уравнение (7). Получим L=∆m+1xm+1+...+∆nxn=L0 (8), где ∆j = c1g1j + c2g2j + ... + cmgmj - cj , j=1,2,...n (9) или ∆j = zj - cj, zj= cigij, j=1,2,...n (9a). Целесообразно ввести вектор C (c1,c2,...cm)`, компонентами которого служат коэффициенты при неизвестных в линейной форме (1), они записываются в том порядке, в котором расположены соответствующие базисные неизвестные в системе уравнений. Тогда, zj можно представить как скалярное произведение ∆j = CGj- cj, j=1,2,...n. А L0 = CH. Для проведения указанных вычислений обычно составляют таблицу (ТАБЛИЦА 1) Ее называют – первой симплекс таблицей. Из Ур-я (8) получаем выражение целевой ф-ии L через свободные неизвестные: L=L0-∆m+1xm+1-...-∆nxn. 16. Симплексный метод ЛП: исследование данного базисного допустимого решения на оптимальность, условия оптимальности в случае минимизируемой и максимизируемой функции цели. Из выражения L=L0-∆m+1xm+1-...-∆nxn (1) следует, что базисное решение x1=h1, x2=h2,...xm=hm, xm+1=0,...xn=0 (2) является оптимальным решением задачи ЛП L=c1x1+c2x2+...cnxn ,при условиях: x 1 + g1,m+1xm+1 + ... + g1nxn = h1,x2 + g2,m+1 xm+1 + ... + g2nxn = h2, ... ... ... ... xm + gm,m+1 xm+1 + ... + gmnxn = hm и xj≥0, j = 1,2,...n, тогда и только тогда, когда в уравнении L=∆m+1xm+1+...+∆nxn=L0 среди коэффициентов ∆j при неизвестных нет ни одного положительного, т.е. условие оптимальности имеет вид: ∆j ≤0, j=1,2,...n. Действительно, если в общем решении xi=hi-gi,m+1xm+1-...-ginxn, i=1,2,...,m мы станем придавать различные неотрицательные значения свободным неизвестным так, чтобы соответствующие базисные неизв-е принимали неотрицательные значения, то одновременно с частными неотрицательными решениями с-мы ограничений будем получать согласно выражению (1), соответствующие им значения целевой ф-ии. В частности, при нулевых значениях свободных неизвестных получится базисное решение (2) и соответствующее ему значение линейной формы L0=c1h1+c2h2+...cmhm+cm+1*0+...+cn*0 = ci hi17. Симплексный метод ЛП: условие единственности базисного оптимального решения. Условие неограниченности целевой ф-ии на множестве допустимых решений. П  ри выполнении условия оптимальности базисное решение x1=h1, x2=h2,...xm=hm, xm+1=0,...xn=0 будет единственным оптимальным решением задачи ЛП тогда, и только тогда, когда все коэффициенты ∆m+1, ∆m+2,…, ∆n при свободных неизвестных в последнем уравнении вспомогательной системы xi +  gijxj = hi , i= 1,2,...m,(1) L + ∆jxj = L0 Строго отрицательны. Если же хотя бы один из коэффициентов при свободных неизвестных равен нулю, то будут и небазисные оптимальные решения. Е  сли есть хотя бы одна свободная неизвестная, такая что коэффициент ∆j при ней в последнем уравнении системы (1) положителен, а в первых m уравнениях той же системы среди коэффициентов g1j, g2j, …gmj при ней нет ни одного положительного, то задача линейного прогрмаммирования неразрешима в силу неограниченности линейной формы L=c1x1+c2x2+...cnxnна множестве неотрицательных решений системы ограниченийx1 + g1,m+1xm+1 + ... + g1nxn = h1, x2 + g2,m+1 xm+1 + ... + g2nxn = h2, (2) ... ... ... ... xm + gm,m+1 xm+1 + ... + gmnxn = hm. 18. симплексный метод ЛП: переход от одного базисного допустимого решения к другому. Правила выбора разрешающей неизвестной и разрешающего уравнения, их обоснование. Монотонность и конечность симплексного алгоритма для невырожденной задачи ЛП, понятие о зацикливании. Тк неизвестная xs при нулевых значениях других свободных неизвестных не может возрастать неограниченно, а целевую ф-ю мы хотим минимизировать, то придадим неизвестной xs наибольше значение, которое она может принять, тем самым выделив из общего решения крайнее неотрицательное решение системы ограничений. Это крайнее решение совпадает с новым базисным неотрицательным решением, соответствующим новому предпочитаемому виду системы, для получения которого достаточно принять неизвестную xs за разрешающую и подвергнуть систему симплексному преобразованию. Если m  in  =  , то за разрешающее Ур-е берем r-е. как только мы получим новое базисное неотрицательное решение системы ограничений, придется это решение исследовать на оптимальность. Процесс перехода к новым и новым решениям продолжается до тех пор, пока не будет получено оптимальное решение (или не будет доказана неограниченность линейной формы на множестве решений системы ограничений, но это утверждение справедливо лишь при условии невырожденности задачи, т.е. ни на одном этапе процесса решения ни один из свободных членов системы ур-й не обращается в нуль. Новое значение линейной формы строго меньше предыдущего и через конечное число шагов мы придем к оптимальному решению (или докажем неразрешимость задачи). В вырожденном случае на одном или нескольких этапах свободный член может оказаться равны нулю, и значение линейной формы не измениться. Появится возможность цикла. 19. Метод искусственного базиса. 21. Основное нерав-во теории двойственности. Для любых допустимых решений х(х1,х2,..хn) и y(y1,y2,..yn) прямой и двойственной задач ЛП справедливо нерав-во:  Док-во:  ( )xj = *. Эта сумма не изменится, если мы поменяем порядок суммирования: *=  ( )yj   ; *  Малая теорема двойственности. Для существования оптимального решения пары двойственных задач необходимо и достаточно существование допустимого решения для каждой из них. Теорема о достаточном условии оптимальности решений пары двойственных задач. Если для некоторых допустимых решений х0 и у0 пары двойственных задач выполнено равенство:  То данные решения являются оптимальными. Экон.смысл: план производства продукции и вектор оценок ресурсов является оптимальным, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают. 22. Первая теорема двойственности. Если одна из задач двойственной пары имеет оптимальное решение, то и др. имеет опт. решение, причем, экстремальные значения линейных форм в обеих задачах совпадают Если же какая-то задача не имеет решения, то система ограничений др. задачи противоречива. Экон.смысл: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения минимальных оценок ресурсов, причем цена продукта, полученного при реализации оптимального плана, совпадает с суммарной оценкой имеющихся ресурсов. 23. Вторая осн.теорема двойственности для того, чтобы допустимые решения х(х1,х2,..хn) и y(y1,y2,..yn) были оптимальными, необходимо и достаточно выполнение следующих условий x0j(  ,  если какое-либо нер-во системы ограничений одной из задач не обращается в точное равенство оптимальным решением этой задачи, то соответствующая компонента оптимального решения двойственной задачи должна быть равна 0. если же к.-л. Компонента оптимального решения положительна, то соотв-ее ей ограничение в двойственной задаче должно быть обращено в точное равенство. Другими словами: 1)если хj0>0,то  aijyi0=cj; 2)если aijyi0>cj , то xj0=0; 3)если yi0>0, то aijxj0=bi; 4)если aijxj0 , i= Если по оптимальному плану расход i-того ресурса < его запасов, то оценка этого ресурса=0. если же оценка>0, то расход этого ресурса равен его запасу. Т.о. дефицитный (полностью используемый по оптимальному плану) ресурс имеет положит.оценку в двойственной задаче, а недефицитный – нулевую оценку. С точки зрения пр-ва: если оценка ресурсов, расходуемых по j-ой технологии больше цены продукта, то j-ая технология не применяется (xj=0). Если же по некот. Плану j-ая технология применяется (xj>0), то оценка ресурсов, расходуемых по данной технологии, равна цене продукта. 24. Третья теорема двойственности. Пусть имеются две пары двойств. Задач, и пусть в исходной задаче величины cj и aij не меняются, а первые части системы ограничений меняются (bi=var), тогда каждому вектору В=(b1,b2,..bm), будет отвечать свое оптимальное решение исходной задачи. Теорема: Значения переменных yi0 в оптимальном решении двойственной задачи представляют собой оценки влияния правых частей bi системы ограничений исходной задачи на величину максимума целевой функции:  zmax/ bi =yi0 , при этом увеличение правой части i-го ограничения приводит к увелич. или уменьш. zmax в зависимости от того будет ли yi0 положит. или отрицательным. Экон.смысл: двойственная оценка ресурса – это приращение прибыли, приходящейся на единицу приращения этого ресурса. 25. Задача о расшивке узких мест пр-ва, ее мат.модель и решение. В задаче планирования производства мы нашли оптимальный план пр-ва и узкие места пр-ва, т.е. те ресурсы кот. используются полностью, они называются дефицитными. Будем расшивать «узкие места» пр-ва, т.е. заказывать дополнительно дефицитные ресурсы. Пусть T(t1,t2,t3)- вектор дополнительных объемов ресурсов, (В+Т) – вектор новых объемов ресурсов. прирост прибыли, приходящийся на ti единиц i-го ресурса, будет равен у*iti, где у*- двойственная оценка этого ресурса. Условие устойчивости двойственных оценок, как видно из соотношения Q-1B=H, характеризуется нерав-ом:H+Q-1T>=0 Составить план расшивки узких мест пр-ва означает указать сколько единиц каждого из дефицитных ресурсов нужно дополнительно заказать, чтобы суммарный прирост прибыли был максимальным. Т.о. проблема расшивки «узких мест» представляет собой задачулинейного программирования: найти план расшивки T (t1, t2, t3), максимизирующий суммарный прирост прибыли: w = y* T, при условиях H+Q-1T>=0 и T>=0. 26.Транспортная задача по критерию стоимости. Транс.задача формулируется следующим образом. Продукт, сосредоточенный в m пунктах производства в кол-ве a1, a2,...,am единиц, необходимо распределить между n пунктами потребления, которым необходимо b1,b2,..,bn единиц. Стоимость перевозки единицы продукта из i-го пункта пр-ва в j-ый пункт потр-ия равна cij. Необходимо составить план перевозок, при кот. запросы всех пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах пр-ва и общие транспортные расходы по доставке были бы минимальны. Обозначим xij кол-во груза, планируемого к перевозке от i-го поставщика j-му потребителю. При балансе произ-ва и потр-я  = математическая модель тр. задачи выглядит так: найти план перевозок Х=(хij), i=1,2,..,m; j=1,2,..,n, минимизирующий общую стоимость всех перевозок L=  ,при условии что из любого пункта вывозится весь продукт:  , i=1,2,..,m. И любому потребителю доставляется необходимое количество груза:  j=1,2,..,n,.. и по смыслу задачи x11>0,..,xmn>0. Преобразование открытой модели в закрытую. Если общий объем производства превышает объем, требуемый всем потребителям, то модель задачи открытая. Для превращения ее в закрытую вводим фиктивный пункт потребления с объемом потребления, равным разнице между объемом пр-ва и потр-я. 27.Методы построения 1-го базисного допуст.решения транспортной задачи. Первое базисное допустимое решение легко построить по правилу «северо-западного» угла. В транспортной таблице должно быть (m+n-1) занятых клеток На очередном шаге берем сев-зап клетку и сравниваем числа, соответствующие этой клетке, стоящие в строке и столбце. Минимальное из них записываем в се-зап клетку и вычитаем его из чисел, стоящих в строке и столбце. Если ноль получился в строке, берем строку, если в столбце, то столбец и повторяем то же самое. 28. Метод потенциалов Заполненные клетки будем называть базисными. Для каждой баз.клетки, лежащей на пересечении строки i и столбца j, напишем уравнение pi+qj=cij. Переменные p и q называют потенциалами, которых (m+n), а уравнений (m+n-1), поэтому одной переменной можно присвоить произвольной значение. - пусть р1=0. Далее для небазисных клеток вычисляем относительные оценочные коэф-ты:  = pi+qj-cij.. Находим max( >0). Решение оптимально если все <=0, если не так, то строим цикл пересчета, кот. начинается и заканчивается выбранной небазисной клеткой. Присвоим знаки вершинам цикла: выбранной небазисной клетке “+“, следующей вершине- “-“, затем знаки чередуются. Среди вершин со знаком “–“ находим наименьшее число. Затем вычитаем его из вершин со знаком “–“ и прибавляем к вершинам со знаком “+“. Допустим, что min достигается в нескольких базисных клетках, тогда выбираем любую, делаем ее небазисной, а во всех остальных ставятся нули.Экон.смысл: оценка свободной клетки показывает, насколько уменьшатся суммарные расходы по перевозке груза, если поставить единицу груза от i-го производителя j-му потребителю 30. Динамическое программирование. ДП разработано для решения задач мат.программирования путем их разложения на относительно небольшие, менее сложные задачи. Для отыскания оптимального управления планируемая операция разделяется на ряд последовательных шагов, т.е. процесс планирования становится многошаговым, причем каждый раз оптимизируется управление только на одном шаге. Принцип оптимальности и реккурентные соотношения. Принцип искать всегда оптимальное продолжение процесса относительно того состояния, которое достигнуто в данный момент, принято называть принципом оптимальности. Параметр состояние и ф-ия состояния. Состояние на каждом шаге характ-ся некоторой переменной величиной, кот. называется параметром состояния. Наилучший эффект на данном этапе вместе с уже рассмотренными шагами хар-ся функцией состояния. Решение конкретной задачи методом динамич. Программирования сводится к выбору параметра состояния, составлению ф-ии состояния и реекурентных соотношений, связывающих ф-ии состояния для двух соседних последовательных этапов, и их применению для выбора оптимального управления. 31. Задача распределения капитальных вложений: постановка, математическая модель и решение методом динамического программирования. Данная задача с n переменными представляется как многошаговый процесс принятия решений. На каждом шаге определяется экстремум функции только от одной переменной. Предположим, что указано n пунктов, где требуется построить или реконструировать предприятия одной отрасли, для чего выделено b рублей. Обозначим через fi(xi) прирост мощности или прибыли на j-м предприятии, если оно получит xi рублей капитальных вложений. Требуется найти такое распределение (x1,x2, ... , xn) капитальных вложений между предприятиями, которое максимизирует суммарный прирост мощности или прибыли z = f1(x1) + f2(х2) + ... + fn(xn) при ограничении по общей сумме капитальных вложений x1 + x2 + ... + xn = b причем будем считать, что все переменные xj принимают только целые неотрицательные значения xj = 0, или 1, или 2, или 3, ... Функции fj(xj) мы считаем заданными, заметив, что их определение - довольно трудоемкая экономическая задача. Воспользуемся методом динамического программирования для решения этой задачи. Динамическое программирование - это вычислительный метод для решения задач управления определенной структуры. Введем параметр состояния и определим функцию состояния. За параметр состояния примем количество рублей, выделяемых нескольким предприятиям, а функцию состояния Fk() определим как максимальную прибыль на первых k предприятиях, если они вместе получают рублей. Параметр может изменяться от 0 до b. Если из рублей k-е предприятие получит xk рублей, то каково бы ни было это значение, остальные - xk рублей естественно распределить между предприятиями от первого до (k-1)-го так, чтобы была получена максимальная прибыль Fk-1( - xk). Тогда прибыль k предприятий будет равна fk(xk) + Fk-1( - xk). Надо выбрать такое значение xk между 0 и , чтобы эта сумма была максимальной, и мы приходим к рекуррентному соотношению Fk()=max{fk(xk) + Fk-1(-xk)} 0 xk для k = 2, 3, 4, ... , n . Если же k=1, то F1() = f1() Рассмотрим пример. Пусть производственное объединение состоит из четырех предприятий (n=4). Общая сумма капитальных вложений равна 700 тыс. рублей (b=700), выделяемые предприятиям суммы кратны 100 тыс. рублей. Значения функций fj(xj) приведены в таблице 1, где, например, число 88 означает, что если третье предприятие получит 600 тыс. руб. капитальных вложений, то прирост прибыли на этом предприятии составит 88 тыс. руб. Таблица I  Прежде всего, заполняем табл. 2. Значения f2(x2) складываем со значениями F1( - x2) = f1(- x2) и на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение  . Заполняем таблицу 3.Продолжая процесс, табулируем функции F3(),  () и т.д. В табл. 6 заполняем только одну диагональ для значения = 700. Наибольшее число на этой диагонали: Zmax = 155 тыс. руб.,причем четвертому предприятию должно быть выделено х*4 =  4 (700) = 300 тыс. руб.На долю остальных трех предприятий остается 400 тыс. руб. Из табл. 5 видно, что третьему предприятию должно быть выделено x*3 = 3 (700-x*4) = 3 (400) = 200 тыс. руб.Продолжая обратный процесс, находим x*2 = 2 (700 - x*4 - x*3) = 2 (200) = 100 тыс. руб.На долю первого предприятия остается x*1 = 700 - x*4 - x*3 - x*2 = 100 тыс. руб. Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям: x*1 =100; x*2 =100; x*3 = 200; x*4 = 300. Оно обеспечивает производственному объединению наибольший возможный прирост прибыли 155 тыс. руб. Студенту рекомендуется проверить выполнение равенства f1(x*1) + f2(x*2) + f3(x*3) + f4(x*4) = z max |