Геотехника вопросы. 1. Состав грунтов. Классификация грунтов

• Название: 1. Состав грунтов. Классификация грунтов
• Дата: 26.12.2021
• Размер: 0.61 Mb.
• Имя файла: Геотехника вопросы.docx
• Тип: Документы; #318967
• страница: 3 из 3

14. Определение напряжений в массиве грунта от сосредоточенной силы.

Составим расчётную схему данной задачи, представив грунтовое основание, как упругое полупространство.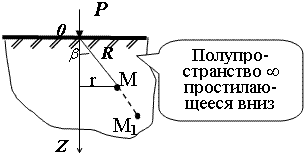



Графическое представление условий (расчётная схема) задачи для определения напряжений в массиве грунта от сосредоточенной силы.

По условиям задачи необходимо определить значения вертикальных напряжений σ_z и касательных напряжений τ_zx; τ_zy в точке М, расположенной на площадке, параллельной плоскости, ограничивающей массив от действия сосредоточенной силы Р.

Решим эту задачу в три этапа:

1. 
   Определим σ_R – в радиальном направлении перпендикулярно R (в т. М)
   
2. 
   Определим σ_R' – в радиальном направлении (приложенном к площадке, параллельной плоскости ограничивающей массив).
   
3. 
   Определим σ_z;τ_zx;τ_zy.
   

1 этап решения задачи:

Допустим, что под действием силы Р точка М переместилась в точку М₁. Обозначим S – перемещение точки М. Тогда можно записать:

Мы получили перемещение точки М (см. выше приведённый рисунок).

В представленной зависимости осадка точки будет прямо пропорционально завесить от косинуса угла β и обратно пропорционально радиусу расположения точки, где А – коэффициент пропорциональности.

Определим относительное перемещение точки: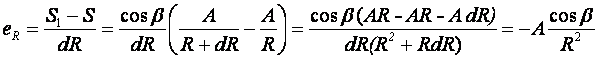



Согласно первому постулату теории упругости между напряжениями и деформациями должна быть прямая зависимость, следовательно:



Радиальное напряжение в точке М.

В этой формуле В – коэффициент пропорциональности. Для определения σ_R необходимо определить произведение коэффициентов АВ.

σ_R – определяется по методу, используемому в сопромате («метод сечений»: мысленно разрезают балку, одну часть отбрасывают и оставшуюся часть уравновешивают).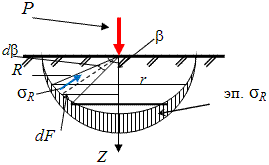



Расчётная схема для определения радиальных напряжений в грунте.

Для решения данной задачи поступим аналогичным образом. Рассматрим полушаровое сечение радиусом R и заменим отброшенное пространство напряжениями σ_R. Рассмотрим изменение β в пределах dβ. Составим уравнение равновесия на ось Z: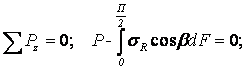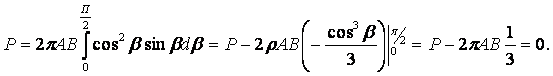









Величина радиального напряжения в грунте зависит от координат точки и величины прикладываемой силы.

2 этап решения задачи: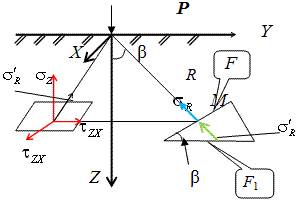



Схема пересчёта радиальных напряжений к вертикальным.

Из геометрических соотношений можно записать: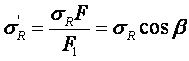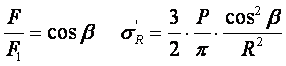







Мы получили величину радиальных напряжений, приложенных к площадке параллельно плоскости, ограничивающей массив.

3 этап решения задачи: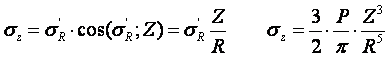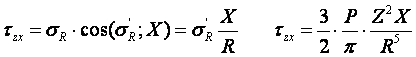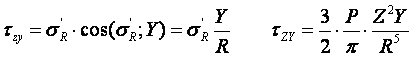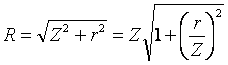







, подставим и получим



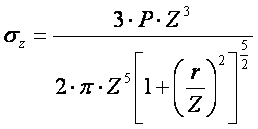Введём обозначение: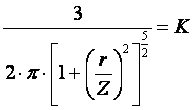



Упрощая выше полученное выражение, вводим значение коэффициента К. Тогда получим: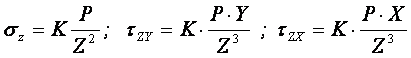



Результат окончательного решения нашей задачи.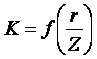

– определяется по таблице.

15. Определение напряжений 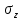– в массиве грунта от действий различных нагрузок.

Рассмотрим r_i элемент загруженный элементарной нагрузкой P_i:

В результате получено напряжение в массиве грунта от воздействия единичного элемента. P_i – нагрузка на данный элемент.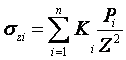



Вертикальное напряжение в точке грунта определяется, как сумма напряжений от единичных элементов.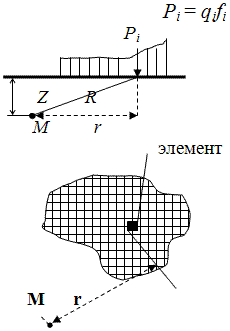



Расчётная схема для определения напряжений от распределённой нагрузки.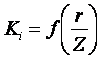



18. Распределение напряжений по подошве фундамента (контактная задача).

Этот вопрос имеет особое значение для гибких фундаментов, рассчитываемых на изгиб.

Если известно Рконт, то загружая этой величиной фундамент, можно легко определять усилия в конструкции тела фундамента.

Из курса сопротивления материалов известно, что напряжения для сжатых конструкций при прямолинейной эпюре определяются по обобщенной формуле:

smax, min =(N/F) +-(M/W)    - но здесь не учитывается работа сжимаемого основания.

Аналитическое решение по определению значений величин контактных напряжений, получено Буссинеску в виде зависимости:



Расчётная схема для решения задачи Буссинеску.

А 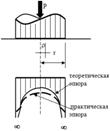нализируя аналитическую зависимость (см. приведённую выше формулу и схему), можно записать, что

При ρ = r → Рρ = ∞

При ρ = 0 → Рρ = 0,5Рср

и построить теоретическую эпюру контактных напряжений. Фактически же, грунт под подошвой фундамента, при давлениях, стремящихся к бесконечности (краевые точки) разрушаясь, приводит к перераспределению напряжений, возникает практическая эпюра (см. приведенную схему). Однако в данной методике также не учитываются свойства грунта основания.

При дальнейших исследованиях было установлено, что эпюра контактных напряжений под подошвой фундамента будет зависеть от его гибкости (Г) - обобщённой характеристики, учитывающей деформативные свойства основания.

Р = f(Г)

Понятие гибкости (Г) было введено профессором Горбуновым-Посадовым М.И.



Е0 – модуль деформации грунта;

ℓ – полудлина фундамента (балки);

Е1 – модуль упругости материала фундамента;

h1 – высота фундамента.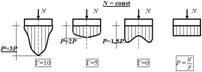



Эпюры контактных напряжений под подошвой фундамента в зависимости от его гибкости. Крайняя правая схема на данном рисунке показывает, что для абсолютно жёстких фундаментов (Г=0), в целях аппроксимации, принята не фактическая седлообразная эпюра контактных напряжений, а прямоугольная (использование аппарата теории упругости к грунтам).

Форма эпюры контактных напряжений зависит и от ширины подошвы фундамента Р = f(b) и при прочих равных условиях (mv – const; N – const) и может быть представлена на следующей схеме: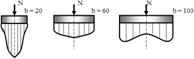



Эпюры контактных напряжений под подошвой фундамента в зависимости от его ширины.

Форма эпюры контактных давлений зависит и от степени нагружения фундамента Р = f (N) и при прочих равных условиях (mv – const; F - const) может быть представлена на следующей схеме: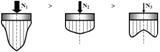



Эпюры контактных напряжений под подошвой фундамента в зависимости от степени нагружения.

Таким образом, приведённые примеры дают наглядную картину изменения величины и формы эпюры контактных напряжений в зависимости от поэтапного нагружения (увеличение веса сооружения в процессе его строительства), что значительно осложняет решение поставленной задачи.

19. Определение напряжений от собственного веса грунта.

Напряжения от собственного веса грунта (или природные, или бытовые давления) определяются для оценки природной уплотненности грунтов и свеженасыпных земляных сооружений.

Природным (бытовым) давлением называют напряжения от веса лежащих выше грунтов в естественных условиях. Эпюра напряжений от собственного веса грунта по глубине для однородных грунтов имеет вид треугольника. Эпюрой этих напряжений для неоднородных грунтов является ломаная линия.

При горизонтальной поверхности и отсутствии бокового расширения грунта напряжение от собственного веса грунта обозначается индексом c_zq и определяется по формуле



где п — число слоев грунта, от веса которых определяется напряжение; у, — удельный вес грунта /-го слоя; А, — толщина /-го слоя.

Рассмотрим эпюры природных давлений для различных оснований (рис.6.39):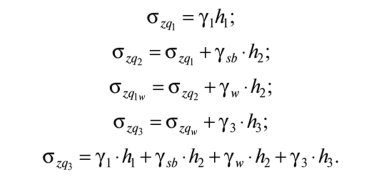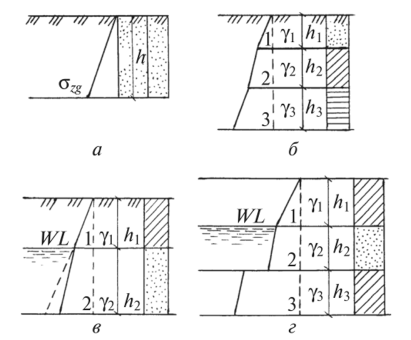 





Рис. 6.39. Эпюры природных напряжений: а — при однородном основании; б — при слоистом основании; в — при наличии подземных вод на глубине б;г — при наличии водонепроницаемого слоя

На грунтовые частицы, находящиеся в воде, действуют собственный вес этих частиц и архимедова сила — сила взвешивания. Архимедова сила равна равнодействующей гидростатического давления воды на частицу и направлена вверх, т.е. противоположно направлению действия собственного веса частиц. С учетом вышесказанного удельный вес взвешенного в воде грунта y_sb определяется по формуле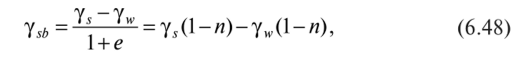



где y_s — удельный вес частиц грунта; y_w — удельный вес воды; е — коэффициент пористости; п — пористость грунта.

Взвешивание грунта водой уменьшает напряжение от собственного веса грунта примерно в 1,5—2 раза. Поэтому при подтоплении территорий пригрузка основания слоем грунта уменьшается и устойчивость сооружений снижается.

Если в толще основания имеется водонепроницаемый грунт (суглинок или глина с J_L< 0,5), то необходимо учитывать давление от столба воды на его кровлю.

Пример 6.12. Построить эпюру вертикальных напряжений от собственного веса грунта, если известно: грунт однородный — песок мелкий; мощность пласта h = 5,0 м; удельный вес грунта у = 19,3 кН/м³; уровень подземных вод (УПВ) находится на глубине 12,0 м.

Решение.

1. Определяем напряжение от собственного веса грунта по формуле (6.35):



2. Строим эпюру напряжений от собственного веса однородного грунта (рис. 6.40).

Пример 6.13. Построить эпюру вертикальных напряжений от собственного веса грунта для геологического разреза, показанного на рис. 6.41, имеющего два слоя:

• 
  • 1-й слой — супеси мощностью И — 6,0 м, удельный вес yi = 17,2 кН/м³;
  
• 
  • 2-й слой — песок мелкий мощностью h₂ = 8,0 м, удельный вес у₂ = 20,0 кН/м³;
  
• 
  • уровень подземных вод — на глубине 20,0 м.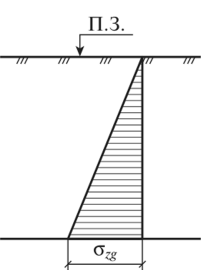
  

Рис. 6.40. К примеру 6.12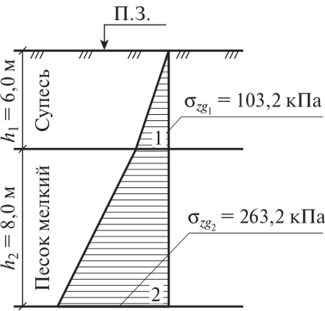



Рис. 6.41. К примеру 6.13

Решение. 1. Определяем напряжение от собственного веса грунта по формуле (6.35) в характерных точках, т.е. на уровне поверхности земли, по подошве I и II слоев: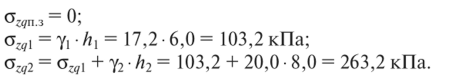



2. Для построения эпюры напряжений от собственного веса откладываем ординаты, соответствующие вычисленным значениям, и соединяем их концы прямыми линиями (см. рис. 6.41).

Эпюра показывает изменение напряжений от собственного веса грунта по глубине. Как видно из рис. 6.41, чем больше удельный вес грунта, тем больше отклонение эпюры от оси.

Пример 6.14. Определить напряжение от собственного веса грунта и построить эпюру (исходные данные — см. пример 6.13). Кроме того, для второго слоя известны: удельный вес частиц грунта y_s2 = 26,6 кН/м³; коэффициент пористости е — 0,65. Уровень подземных вод — на глубине 6,0 м, т.е. второй слой насыщен водой.

Решение. 1. Определяем напряжения от собственного веса в характерных точках по формуле (6.35):

®zqn.3 0,

a_zqi = Y-hi = 17,2 • 6,0 = 103,2 кПа;

c_zq2⁼ G_Zq + Ysbi • ^2 ⁼ 103,2 + 10,1 • 8,0 = 184,0 кПа.

Удельный вес грунта во взвешенном состоянии определяем по формуле (6.36):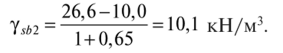



2. Строим эпюру напряжений от собственного веса грунта (рис. 6.42).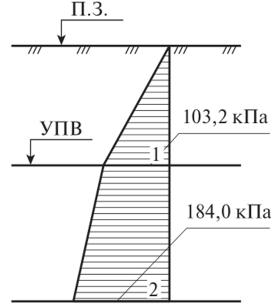



Рис. 6.42. К примеру 6.14

Пример 6.15. Построить эпюру напряжений от собственного веса грунта для геологического разреза, приведенного на рис. 6.43, имеющего три слоя:

• 
  • 1-й слой — песок пылеватый мощностью 5,0 м, удельный вес 17,6 кН/м³;
  
• 
  • 2-й слой — песок мелкий, насыщенный водой, мощностью 7,5 м, удельный вес 18,5 кН/м³, удельный вес частиц грунта 26,8 кН/м³, коэффициент пористости е = 0,69;
  
• 
  • 3-й слой — глина твердая (водоупор) мощностью 6,2 м; удельный вес 19,4 кН/м³;
  
• 
  • уровень подземных вод находится на глубине 8,0 м.
  

Решение. 1. Определяем напряжение от собственного веса грунта по формуле (6.35):



2. Определяем удельный вес грунта во взвешенном состоянии по формуле (6.36):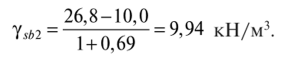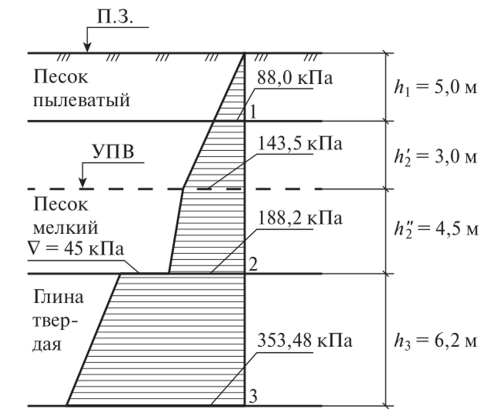





Рис. 6.43. К примеру 6.15

3. Определяем давление столба воды на третий слой, так как данный грунт является водоупором.

Следовательно, взвешивающее действие воды в глине проявляться не будет, но на кровлю глины, помимо давления от вышележащих слоев грунта, добавится гидростатическое напряжение от столба воды, находящегося над слоем глины:



4. Определяем природное давление по подошве третьего слоя: