Шпоры АЭПТПМ. 1. Статические нагрузки двухконцевых лебедок

• Название: 1. Статические нагрузки двухконцевых лебедок
• Анкор: Шпоры АЭПТПМ.doc
• Дата: 15.08.2018
• Размер: 2.32 Mb.
• Имя файла: Шпоры АЭПТПМ.doc
• Тип: Документы; #23002

1.Статические нагрузки двухконцевых лебедок

Одноконцевые лебедки в отличие от двухконцевых являются неуравновешенными механизмами. При подъеме такой механизм кроме полезного груза поднимает канаты, грузозахватывающее устройство, при отпускании в дополнение к грузу он тормозит и т.д., т.е. совершается лишняя работа, механизм дополнительно потребляет эл.энергию, увеличивается мощность Р эл.оборудования и эксплуатационные затраты.
Если число уравнений больше 2 (лифты), то вместо 2ой кабины навешивается балансировочный контргруз (противовес) – G_пр:

G_пр = G₀ + α G_п (1) , где α – коэффициент уравновешивания.

В 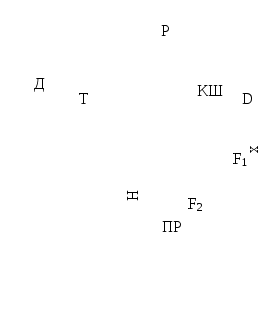качестве примера рассмотрим лифтовую лебедку с червячным редуктором и канатоведущим шкивом.

Д – двигатель

Т – тормоз

Р – редуктор

КШ – канатоведущий шкив

ПР – противовес

К – кабина

│| – уравновешивающие канаты

Результат усилия на канатоведущем шкиве определяется разностью натяжений подвесных канатов: F = F₁ – F₂ (2)

С учетом сил трения F’_тр и F’’_тр в направлениях кабины и противовеса, а также веса канатов с весом погонного тетрад соотношение (2) будет

F = G+G₀ +g_кх –G₀ – αG_п – (H–х)g_к ± (F’_тр –F’’_тр),

«+» – подъем, «–» – спуск F = G + g_к(2х – H) ± F_тр2 – αG_п (3)

Из (3) следует, что усилие на валу шкива будет состоять из усилий, обусловленных весом груза (активных) и силой трения (реактивной).

На валу двигателя эти силы будут составлять момент

М_с = [G + g_к(2х – H) – αG_п] D / (2i_p) ± М_гр (4)

Из (4) видно, что М_с зависит от α и от высоты подъема Н и загрузки кабины G. Если Н невелико или используется уравновешивающие канаты, то составляющей g_к(2х – H) пренебрегаем

М_с = (G – αG_п) D / (2i_p) ± М_гр (5)

Рассмотрим реакции опор двухконцевых лебедок

1. Подъем номинального груза (G = G_н) (6)

2. Подъем пустой кабины (G = 0) (7)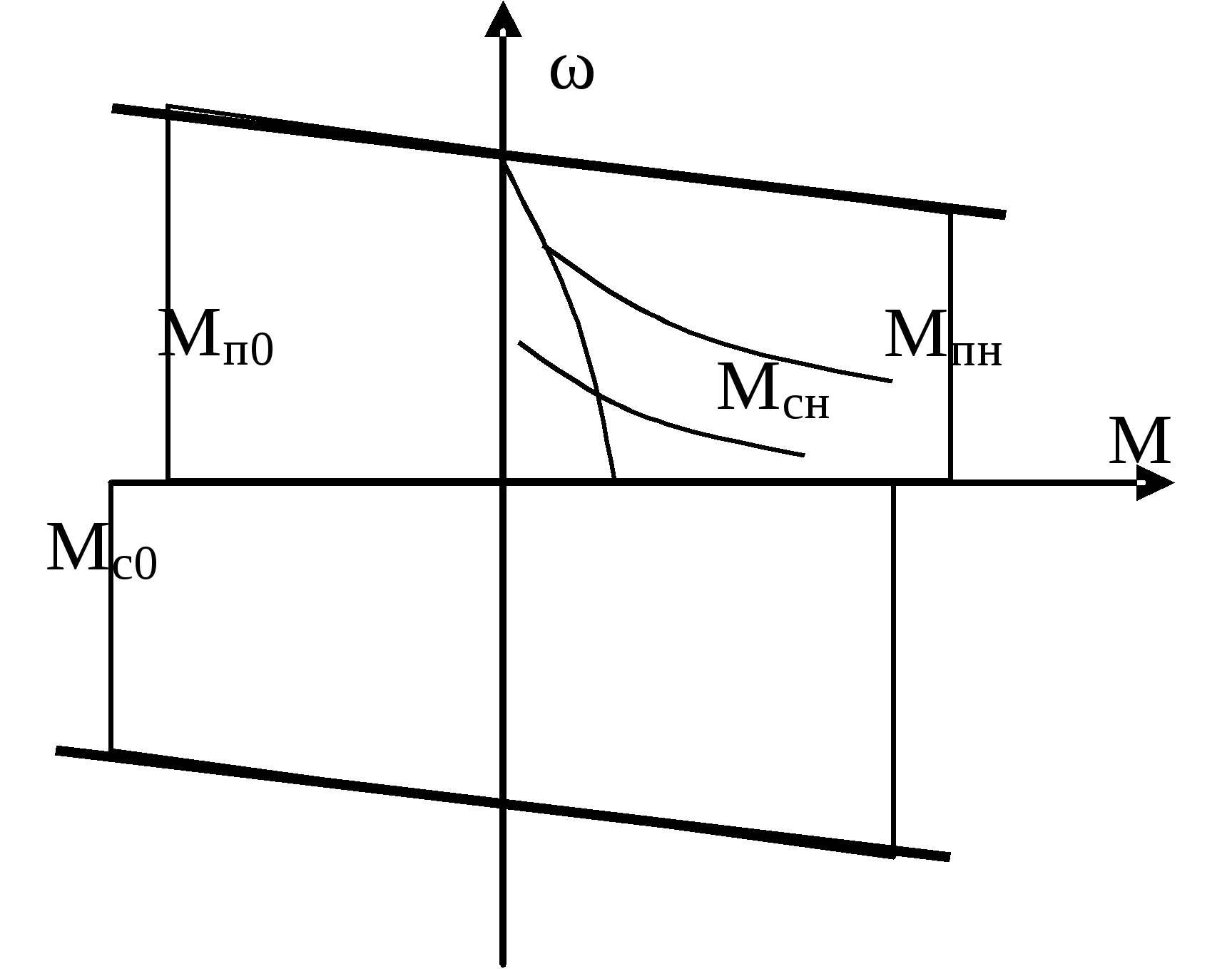

3. Спуск (G = G_н) (8)

4. Спуск (G = 0) (двигательный режим) (9)

Влияние коэффициента уравновешивания α на требуемую мощность оценим с помощью момента среднеквадратического. Зададимся циклом работы, когда лебедка поднимает номинальный груз за время t_п G_н ; t_с G₀. Считаем, время спуска равно подъему.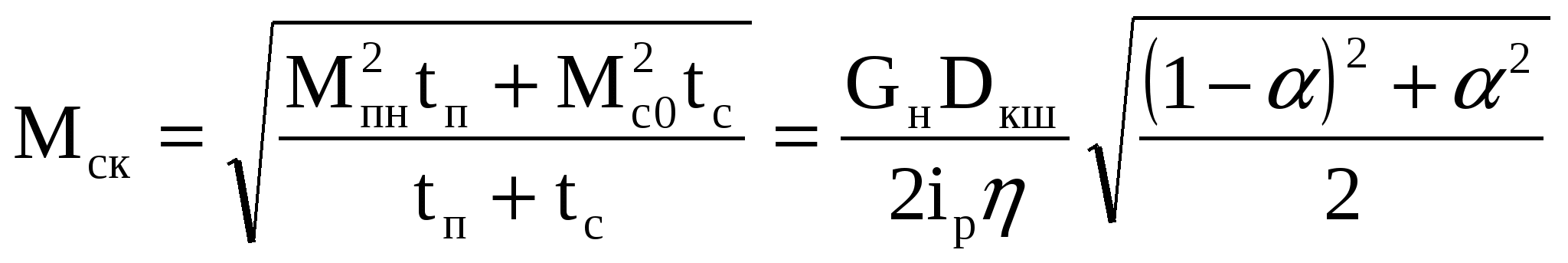

(10)

При выводе считаем , М_ск = f (α)

Для нахождения минимума найдем производную dМ_ск/dα = 0, решение α_опт = 0,5.

М_{ск (α=0)} / М_{ск (α=0)} =

Нагрузки – симметричны относительно начала координат.

2.Методы предварительного выбора типовых ОПМ

Выбор мощности двигателя методом средних потерь и эквивалентных величин (ток, момент, мощность) носит поверочный характер. Число поверочных расчетов зависит от точности выбора запаса на динамические нагрузки. Особенность выбора мощн. типовых ОПМ – динамические нагрузки известны и число поверочных расчетов можно уменьшить. При выборе мощности все ОПМ делятся на 3 группы:

1 группа. Механизмы с малыми инерционными массами и малой частотой включения в час (одноконцевые лебедки)

Дано: М_с = f(t) – нагр.диаграмма мех-ма; ω_р – рабочая скорость; ε_доп – допустимое ускор.

Д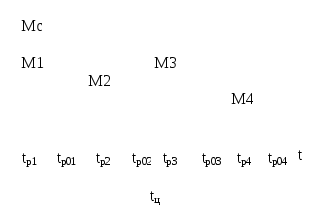ля выбора двигателя в повторно-кратковременном режиме необходимо

1)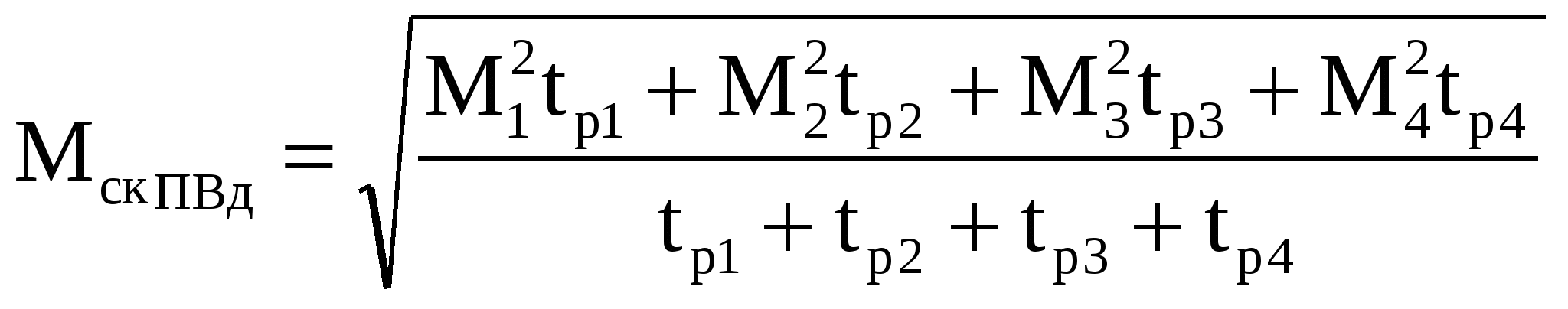

2) 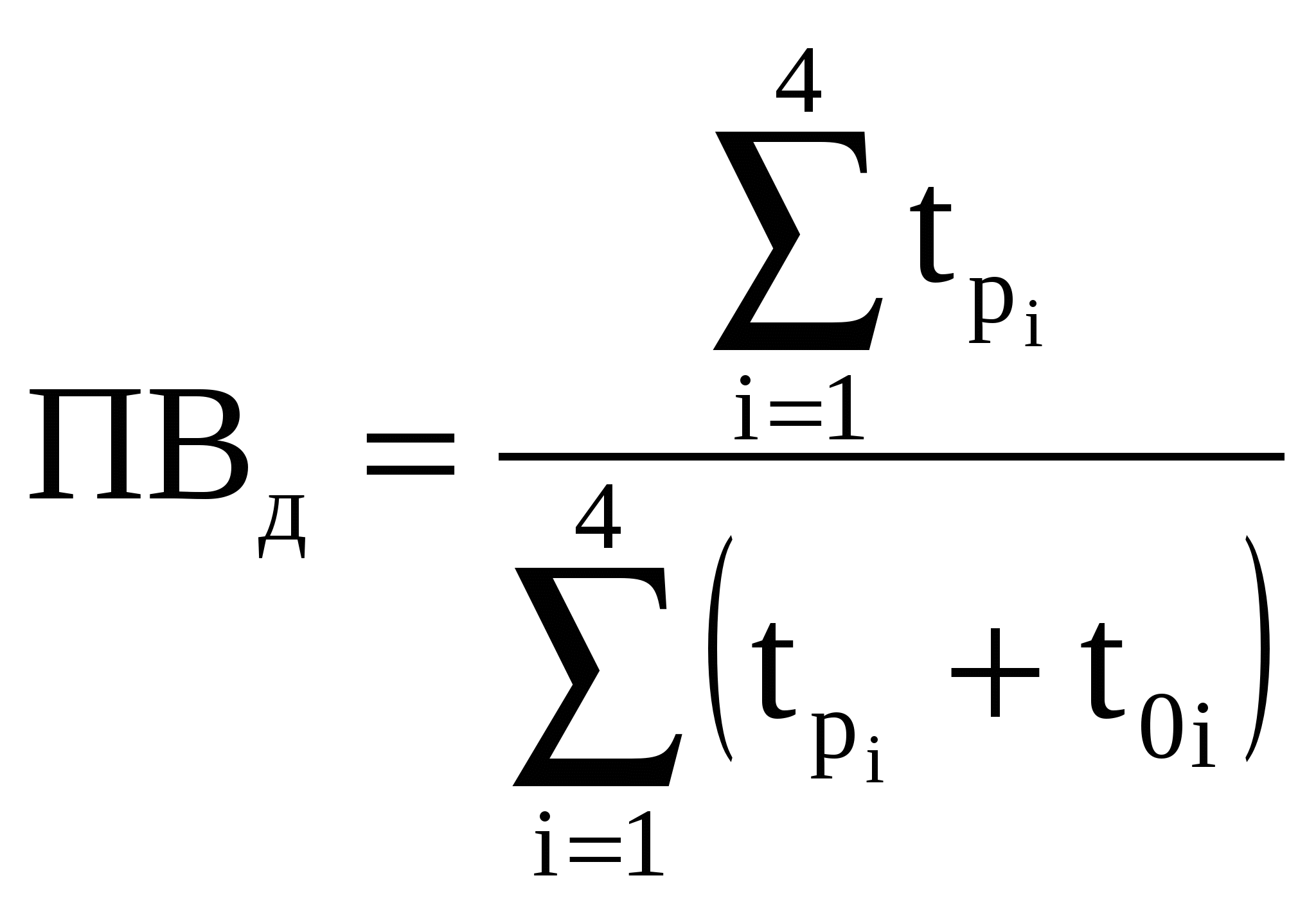3)

4) , К_д = 1,1…1,5, t_п – время пуска

К_д = 1,1  t_п/ t_уст < 0,05; К_д = 1,5  t_п/ t_уст > 0,2…0,3
2 группа. Механизмы с большими инерционными массами (перемещения и поворота, двухконцевые лебедки)

Этот метод может также использоваться для механизмов с малыми инерц.массами и большим числом включений в час.

Дано: М_с = f(t) – нагр.диагр.; ω_р ; ε_доп ; φ_р – рабочий угол φ_р(l_p, H­_p), N – продолж.вкл.

1) Сначала рассчитаем нагрузочную диаграмму двигателя

При пуске М_п = М_с + J_двε_доп + J_мε_доп/η_мех

При торможении М_т = М_с + J_двε_доп + J_мε_допη_мех ; М_уст = М_с

Момент инерции берется равным моменту инерции аналогичных механизмов

2) t_п = t_т ω_p/ε_доп

3) Время поворота в перех.режимах

4) Расчет параметров установившегося движения ;

5) 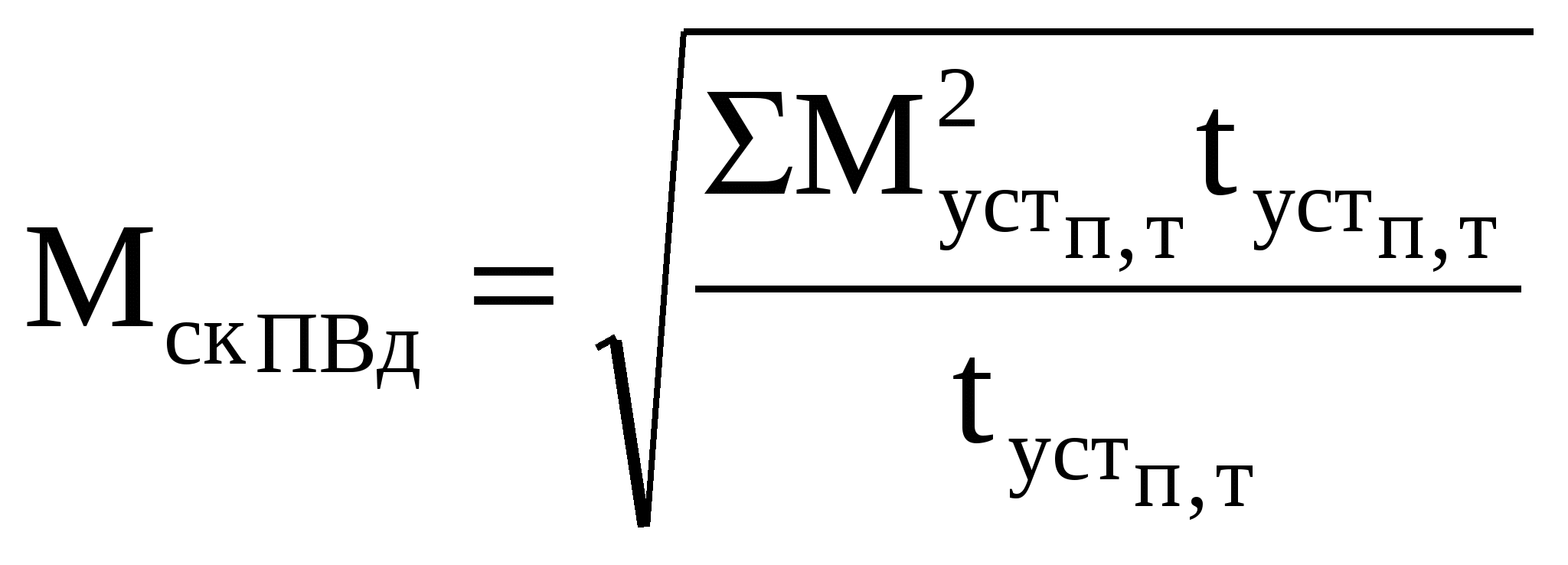6)

7) 8) 9)

3 группа. Цикл работы заданием не определен (механизмы кранов небольшой г/п)

М_макс  t_p1 ; М_мин  t_p2 ; t_p1 = t_p2

ПВ для данных механизмов определяется из среднестатистических значений (краны металлообрабат. станков – ПВ_станд=0,25; лифты – ПВ_ст = 0,6)

Среднедопускаемое использ-е мех-ма			ПВ %	Ср.число вкл.в час	Темпер. окр.среды, оС
По г/п	По времени в течение
Кгп	года, Кг	суток, Кс
0,25…1 0,75 0,75…1 1,0	нерегулируем. 0,5 1 1,0	редк.работа 0,33 0,66 1,0	15…25 25…40 40 60	до 60 60…120 120…240 300…600	25 25 40 45

3.Способы уменьшения механических колебаний

1) ;

Из уравнений следует, что уменьшить колебания можно путем ↓ ε_ср, т.е.нужно ↓ М_пуск (двигатель должен иметь регулируемый пусковой момент), увеличить время пуска, уменьшить производительность.
2) Раскачивание груза можно предотвратить, если в момент времени π/ω₀ со стороны двигателя приложить двойной М_пуск. Обратного отклонения не происходит, дальнейшее движение груза происходит с двойным начальным ускорением.

Для реализации этого нужно, чтобы дв-ль имел изменяемый М_пуск с диапазоном D = 2
3) Уменьшить амплитуду колебаний путем формирования определенного закона управления по времени динамического момента

М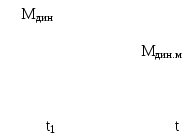_дин.м – макс.момент; t₁ – время разгона до макс.момента

(1)

Запишем ур-е движения такой 2-хмассовой сист. Из схемы замещения запишем ур-е движения отн-но тела массой J₁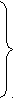

1 / J₁ (2)

Движение тела с массой J2 – 1 / J₂ (3)

– дифференцируем дважды (4)

Получим

(5); (6)

Ур-е (2) делим на J₁, (3) – на J₂, (2)–(3) и в правую часть подставим (6):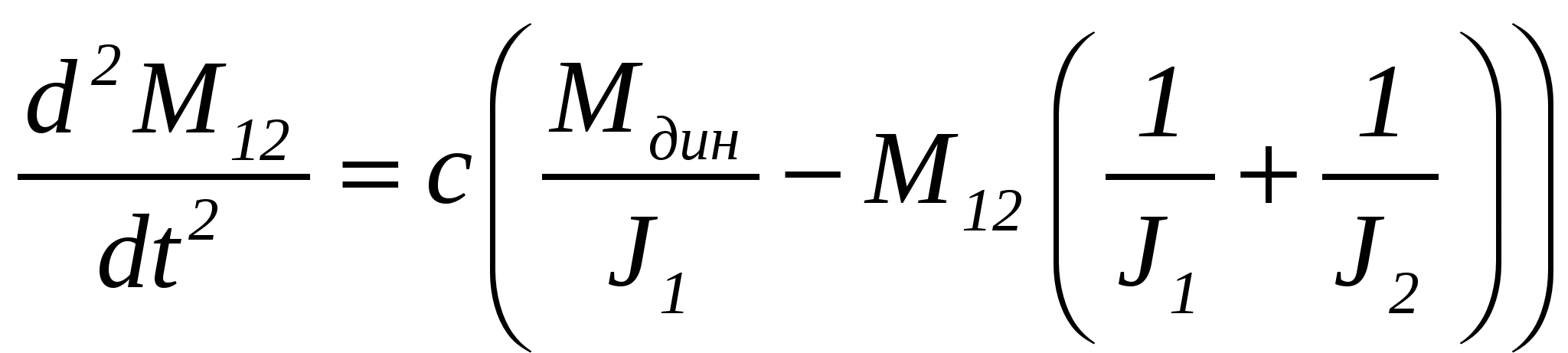


М_динJ₂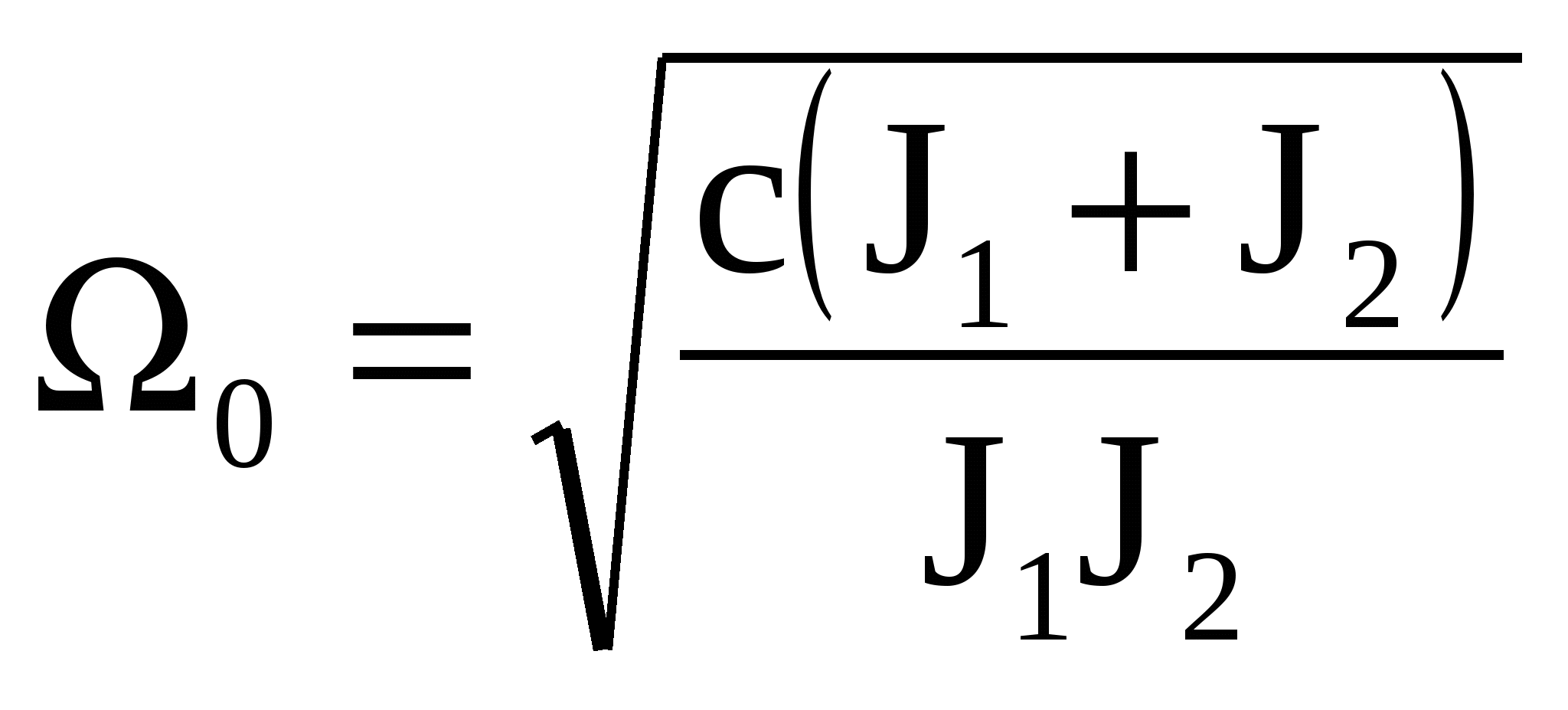
(7)

– частота свободных колебаний 2–х массовой упругой системы

Корни ХУ 2го порядка: р_1,2 = ±jΩ₀ .

Общее решение ур-я (7) : .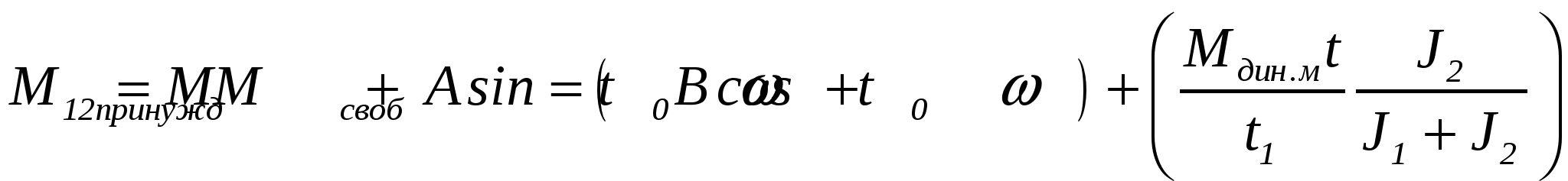

Коэф. А, В из нач.условий (t = 0, M_н = 0): В = 0, 

, А₁ – при постепенном измен.дин.мом.; А₂ – при скачкообразном

1) Чем ↑время нарастания момента t₁, тем ↓ амплитуда отклонений от средней при пуске

2)

3) Ограничение темпа нарастания момента ограничивает и первую производную от ускорения, что хорошо для переходных процессов.

4.Выбор зазоров в зубчатых передачах

Схема замещения

J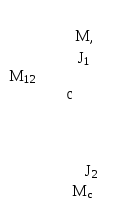₁ – момент инерции двиг + жестко связанный с ним момент инерции тормоза и редуктора; _С – жесткость выходного вала редуктора

Δφ – привед. к валу двиг. зазор передачи

J₂ – момент инерции поворотной платформы с грузом
Процесс выбора зазоров разделяется на 2 этапа:

1) Собственно процесс выбора. В период выбора мех.связь между J₁ и J₂ отсутствует и под действием М происходит разгон масс J₁. Если М=cosnt, то . (1)

Т.к. основные инерц.массы J2 неподвижны, выбор зазора заканчивается ударом, т.е. вся кин.энергия вращающихся масс J1 со скоростью ω_0нач превращается в энергю упругих колебаний и частично рассеивается в деформируемых массах J1 и J2 (диссипативная составляющая колебаний)

2) Если совместить начало отсчета с временем t₁ (t=t₁), когда маховые массы соприкоснутся, то получим: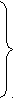

1 / J₁ (2)

J2 – 1 / J₂ (3)

(4)

Считаем, М = const и Мс = const. Получим

(5); (6)

Ур-е (2) делим на J₁, (3) – на J₂, (1)–(2) и в правую часть подставим (6):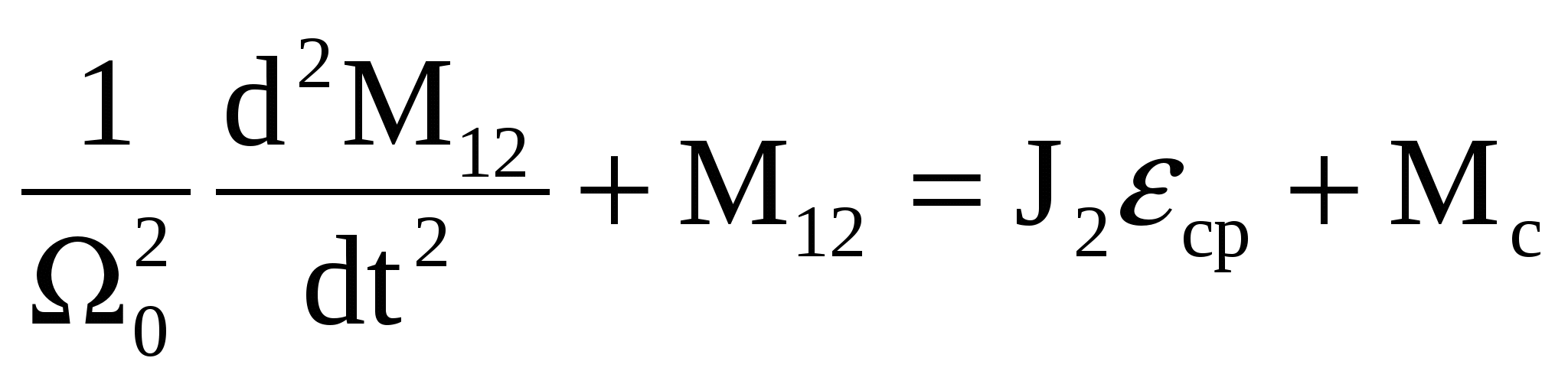

; – среднее ускорение

Найдем М₁₂ : ;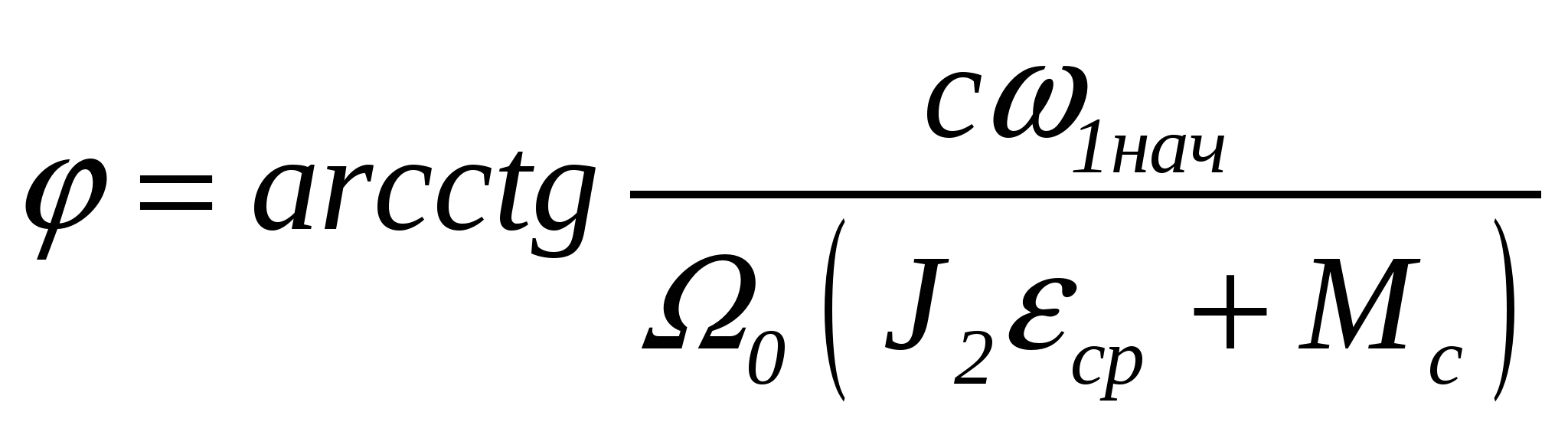

Получим

Для наглядности изобразим это на эпюрах.



Выбор зазора сопровождается многократным зазорообразованием (–ω₁; –М₁₂)

Динамический коэффициент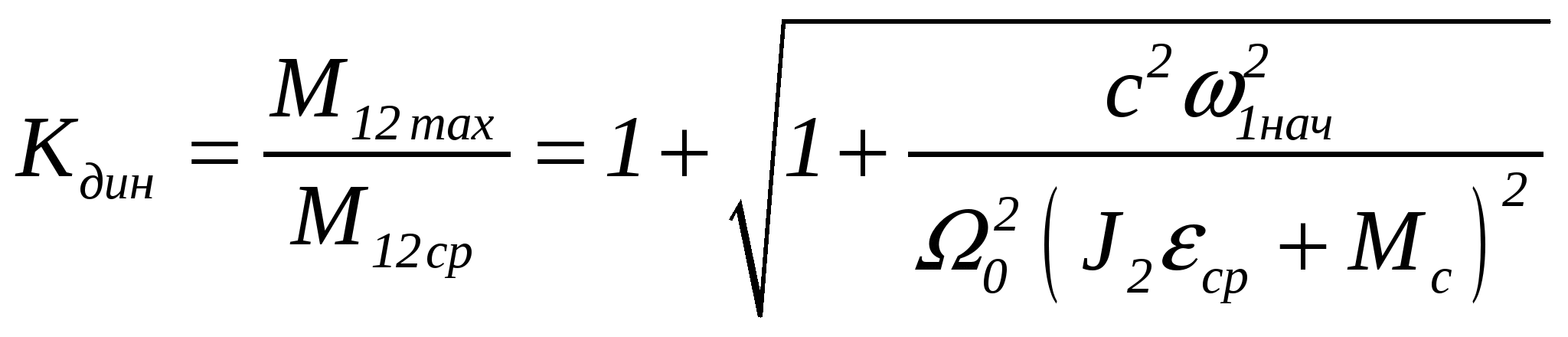

Значит Мmax будет при выборе зазоров как минимум в 2 раза больше среднего момента.

Преобразуем –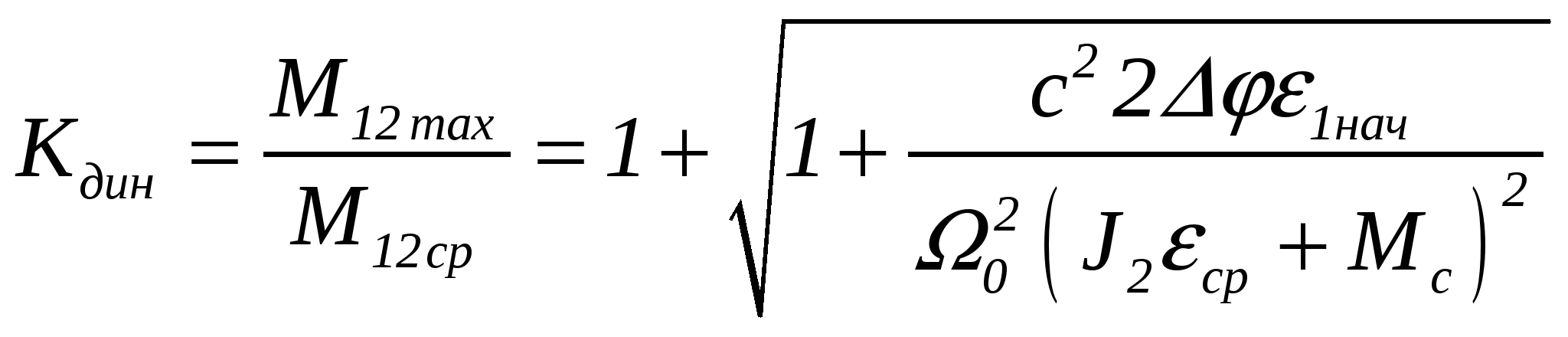

Отсюда следует, что единственный способ уменьшить перегрузки при выборе зазоров – воздействие на ↓ ε_1нач = М/J₁.

5.Электромеханические колебания резонансного характера

Свойственная зубчатой передаче неравномерность хода порождает периоды возмущения с частотой перехода с зуба на зуб. Если J₁>>J₂, то это не скажется на работе ЭП. При J₂>>J₁ возмущения в передаче оказывают существенное влияние на колебания J₁.

Рассмотрим условия возникновения колебаний на механизме поворота. Частота колебаний

, Zзв – число зубьев зубчатого венца.

Рассматриваемые мех-мы представим в виде 2-хмассовой системы, склонной к колебаниям с частотой Ω₀.

При таких условиях даже небольшие возмущения, но с частотой , могут вызвать значительные колебания мех.системы – резонанс.
Средствами ЭП можно уменьшить эти колебания:

1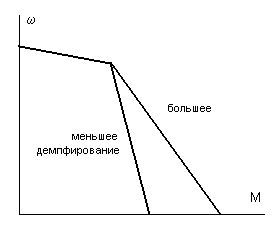. Линейная связь между скоростью и моментом подобна вязкому трению, поэтому воздействовать на колебания резонансного характера можно регулированием наклона падающего участка мех.х-ки. Большее демпфирование при как можно меньше наклоне.

2. Lяц ↓ демпфирование:

а) ↓ действующее значение тока за счет ↑ индуктивного сопротивления;

б) сдвигает по фазе ток (момент) относительно колебаний скорости.

Однодвигательеый привод ↑ нагрузки до 40% М_пуск.



В многодвигательных ЭП повышается производительность механизмов, например мех-м поворота позволяет уменьшить нагрузку на зубчатый венец.
При последовательном соединении двигателей они обтекаются одним током

е_г = е_д1 + е_д2 + i_яR_∑ 
Однако в динамике при протекании ω₁ и ω₂ в противофазе не проявляется и динамические перегрузки превышают среднее значение в 2 и более раз (ω₁↓, ω₂↑ – изменения I не будет).
При параллельном соединении даже при колебаниях ω₁ и ω₂ в противофазе есть контур замыкания для каждого тока, т.е. демпфирование ЭП есть в любом случае.

Достоинства || соединения – динамические нагрузки можно уменьшить.
Т.к. динамические нагрузки больше статических, более эффективно || соед. двигателей.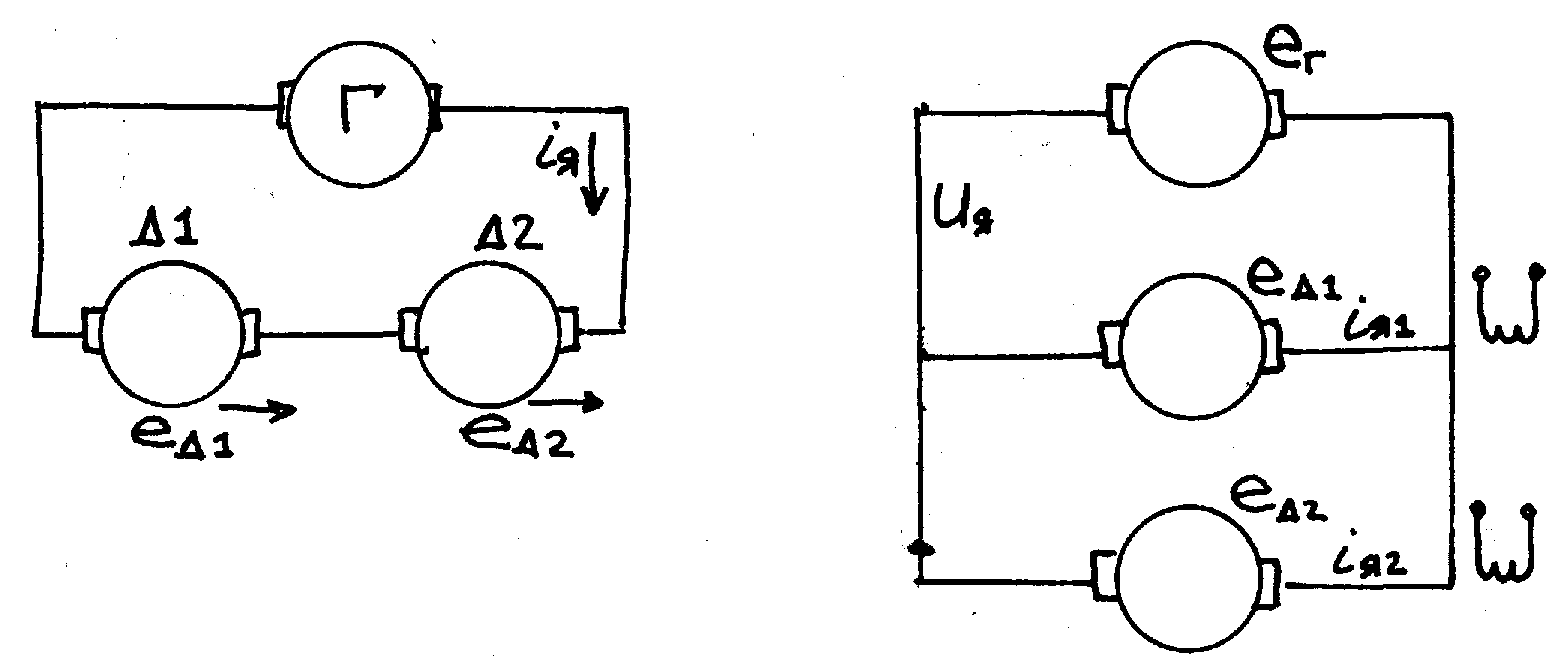



Последовательное и параллельное соединение двигателей

6.Схема безопасного спуска для крановых механизмов с ДПТ ПВ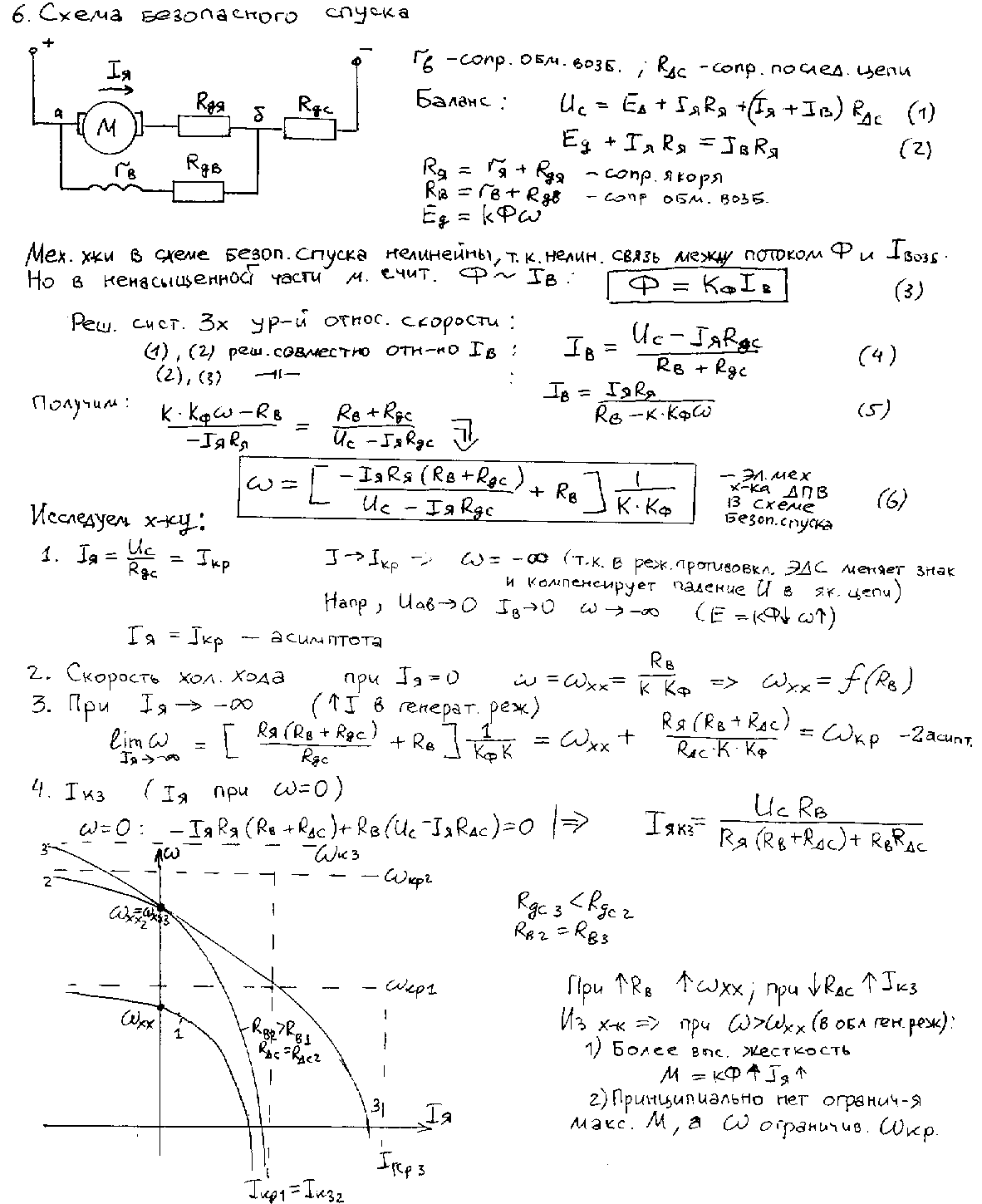

7. Требования, предъявляемые к ЭП экскаваторов. ЭП механизма подъема экскаватора с магнитным усилителем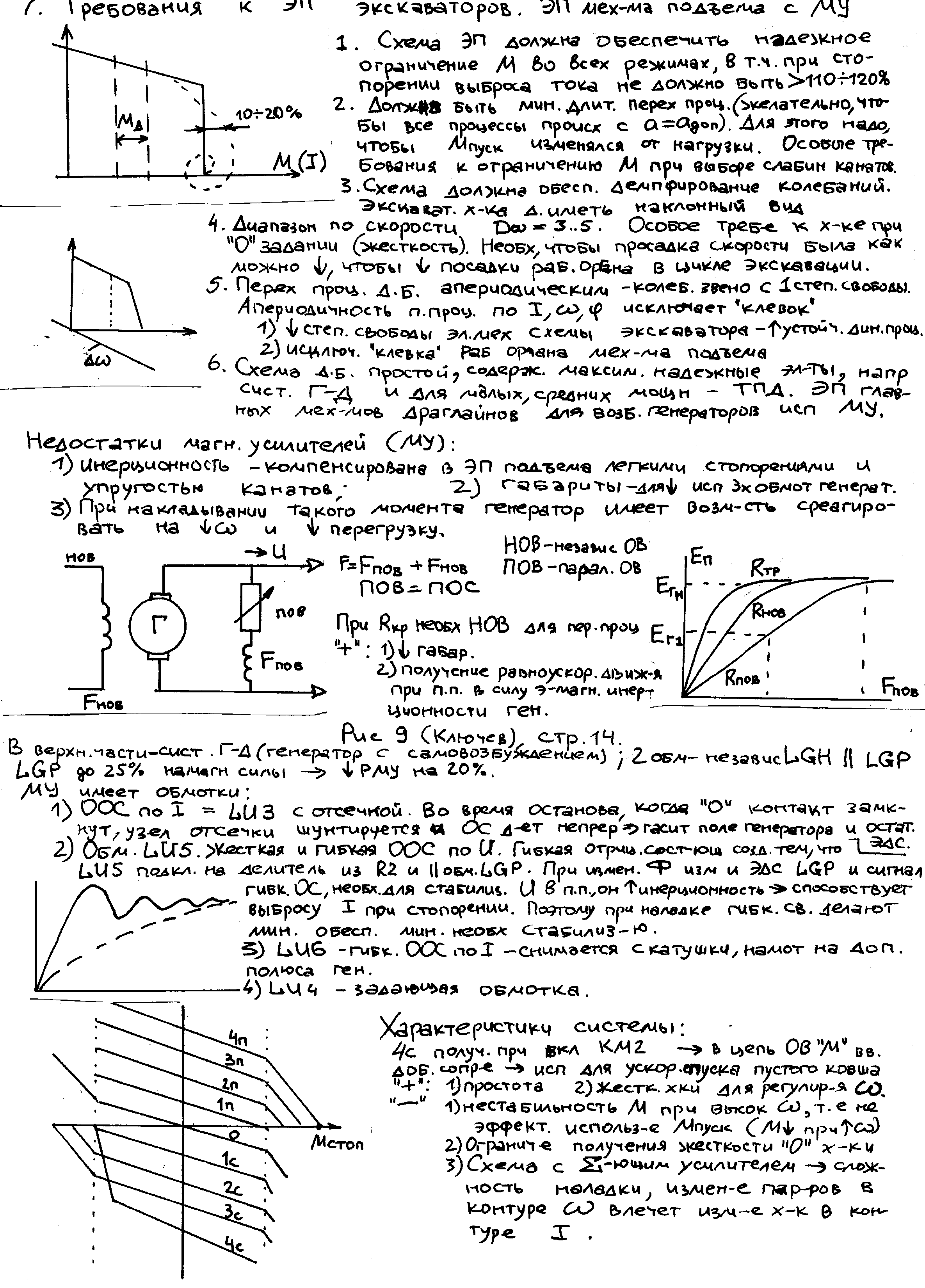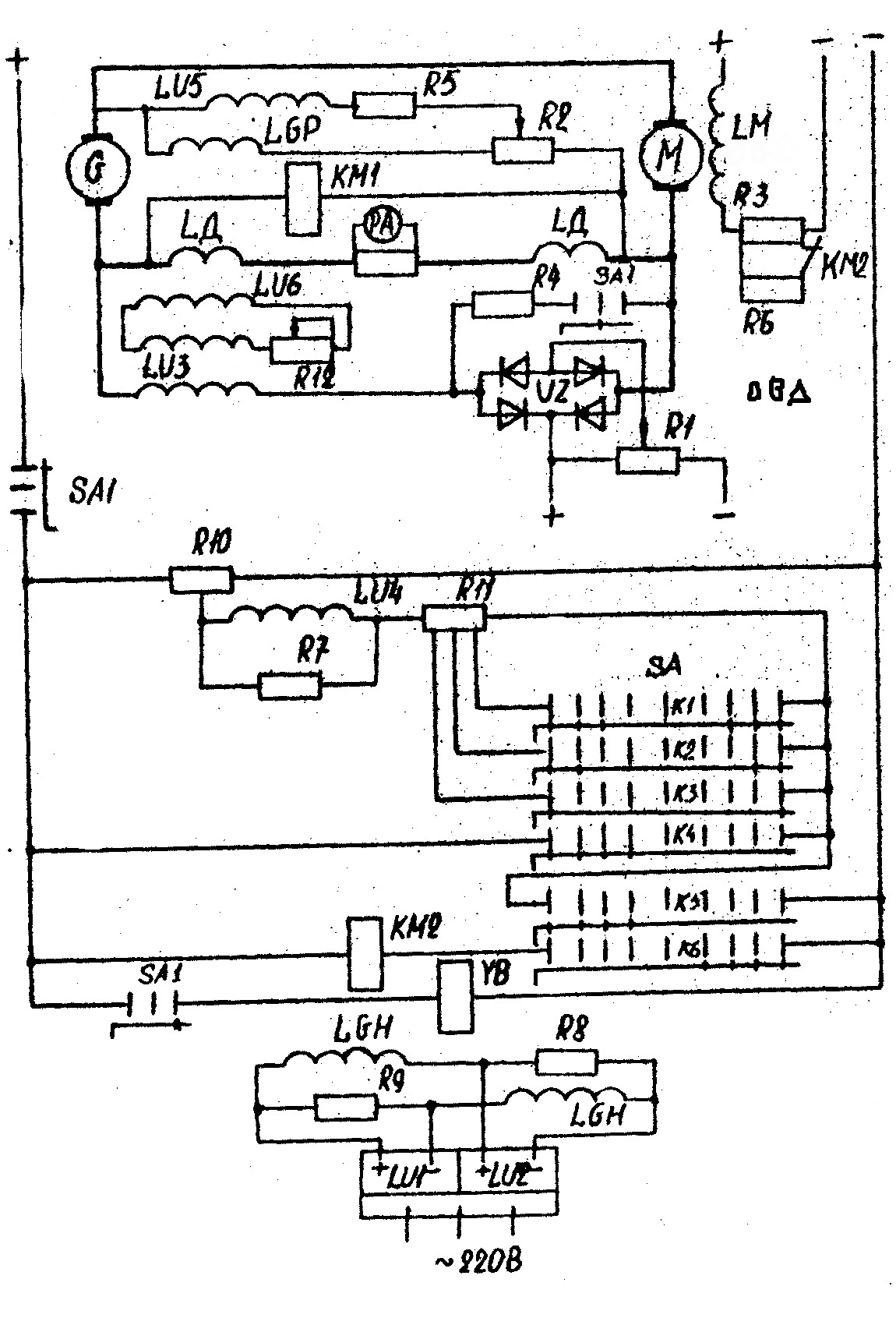

(
ОВД
Рис. к вопросу 7)

Принципиальная схема электропривода механизма подъема экскаватора с магнитным усилителем.

8.Оптимальная структура экскаваторного ЭП. Режим К3

9.Автоматизация подъемно-транспортных механизмов циклического действия

Необходимое условие автоматизации – наличие определенного числа фиксированных остановок. Тогда весь рабочий процесс будет состоять из отдельных циклов.

КШ – канатоведущий шкив

Некоторые механизмы, например перемещения мостового крана, требуют число фиксированных остановок больше 2. Независимо от числа остановок рабочие циклы отличаются лишь исходными и конечными положениями, загрузкой и временем пауз и рабочих движений. Однако в технологическом смысле все циклы одинаковы и состоят из этапов: пуск; перемотка на заданное расстояние; торможение; останов с заданной точностью.

Предъявляются следующие требования к ЭП:

1. Ограничение ускорений во всех режимах

Предъявляется ко всем ПТМ, но по разным причинам:

В ПТМ для перемещения людей ускорение ограничено т.н. «комфортабельным» ускорением (замедлением), при котором человек независимо от возраста и здоровья не испытывает неприятных ощущений. Это ускорение не постоянно. Для пассажирских лифтов – 1,5 м/с²; скоростных – 2…2,5 м/с²; шахтные подъемники (вертикальные) – 0,75; (наклонные) – 0,5.

Для ПТМ не для перевозки людей имеется ограничение по ускорению по нагрузке на металлоконструкции. Для Г/П механизмов для перевозки грузов и имеющих упругие элементы ускорение ограничено величиной колебаний.

2. Необходимость точной остановки

Для пассажирских лифтов точная остановка необходима для удобства и безопасности и сокращения входа (выхода) пассажиров. Чем скоростнее и грузоподъемнее лифт, тем выше точность останова.

Для грузовых ПТМ точность обеспечивает технологический процесс погрузки, выгрузки. Если рабочий орган – скип, то условие точности – погрузка, выгрузка скипа, для вагонетки – необходима точность для этажной площадки.

Во всех случаях нет необходимой точности остановки. Всегда указывается разброс:лифты тихоходные, быстроходные – ±35…50 мм; скоростные ±10…20; больничные ±10;грузовые подъемники: шахтные клетевые – ±100 мм; с вагонетками на рельсах – ±5 мм; шахтные скиповые – ±300 мм.

3. Ограничение рывка.

Точный останов

При автоматизации процесса точного останова действие оператора исключается. Процесс останова начинается с поступления в схему управления импульса с путевого датчика точной остановки (ДТО). Двигатель отключается, накладывается тормоз и далее процесс неуправляем.

Если принять, что отключение двигателя и наложение тормоза происходит одновременно и тормоз прикладывается скачком, весь процесс точного останова делится на 2 этапа:

1 этап обусловлен запаздыванием схемы управления, т.е. двигатель отключается через некоторое время t_зап и рабочий орган (РО) проходит расстояние S₁ = v_нач t_зап;

где v_нач – скорость, с которой РО подошел к ДТО.

2 этап – после отключения двигателя и наложения тормоза. Вся кинетическая энергия поступательного и вращательного движущихся масс расходуется на пути торможения под действием сил сопротивления нагрузки и тормоза. Баланс энергии на этом участке:

, где – суммарная масса вращающихся и поступательных движущихся масс; – радиус приведения; J_Σ – суммарные маховые массы, приведенные к валу дв.;

F_т – усилие сопротивления движению, создаваемое тормозом;

F_c = M_c/R_пр – усилие сил сопротивлений, создаваемое моментом статической нагрузки;

М_с – момент сил сопротивления, приведенный к валу двигателя.

Таким образом, весь путь, проходимый рабочим органом: ; Fдин = F_c + F_т.

Величины, определяющие полный путь, непостоянны:

v_нач зависит от загрузки рабочего органа (РО) и Uсети; t_зап – от температуры Uсети (время работы, смазка); m_Σ – от загрузки РО; F_дин – от загрузки и разброса усилий тормоза.

10. Динамика автоматизированных ЭП ПТМ. Определение необходимости регулирования пускового момента

При повторно- кратковременном режиме, особенно с большим числом вкл. в час производительность ПТМ в значительной степени зависит от времени перех. процесса. поскольку макс. Ускорение ограничено (a=a_доп), то оптимальными будут переходные процессы при а_доп.

Наиб. сильное возмущение, влияющее на ускорение, - М_с и J_. Из уравнения динамики пуск. моменты при наличии возмущения без изменений в пределах: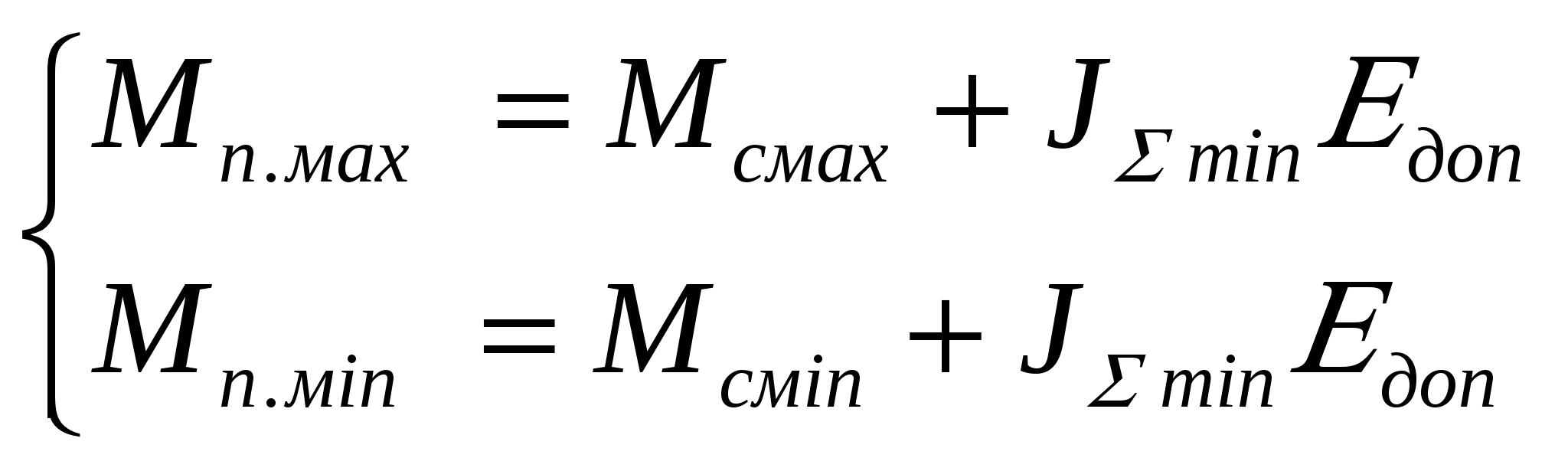



Дле реализации таких оптимальных п/п (a=a_доп) необходимо, чтобы М_пуск автоматически при изм. возмущения от М_пmin до М_пmax. Такими свойствами обладают регулируемые ЭП с обратными связями (в частности, по ускор.). реализация на практике таких ЭП для ПТМ затруднительна, поэтому стремятся использовать простые ЭП, учитывая Е_доп – max допуст.

Условия когда можно ипользовать перерегулирование по М_пуск ЭП: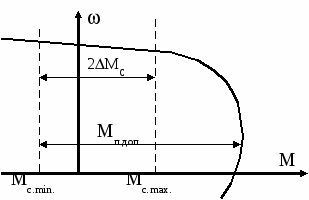




Простейшая хар-ка – АД к/з (S_к=1)



M_{п доп}=М_{с min}+J_minE_доп

При остальных нагрузках ускор. < Е_доп

Мин. ускор. –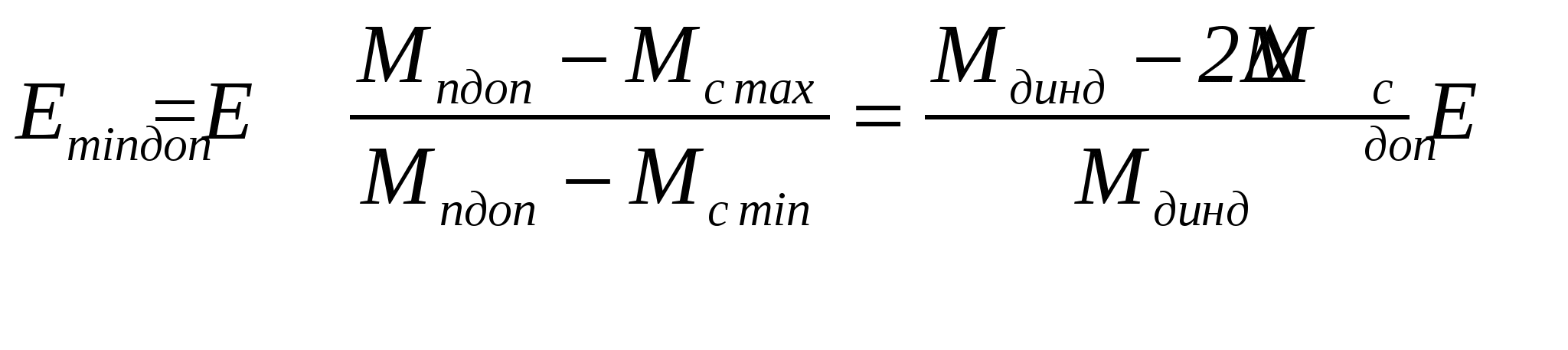

Возможны случаи:

1. М_динд>>2М_сЕ_min Е_доп

Ускорение при работе мех-ма изменяется в незначительных пределах, и max производительность мех-ма обеспечивается при использовании простейших систем ЭП с нерегулируемым М_пуск.

2. М_динд>2М_с

Ускорение изменяется в широких пределах, при этом значительное снижение ускорения при больших нагрузках может недопустимо снижать производительность механизма. Если при М_динд=2М_с а_мин=0, то осуществить пуск при max нагрузке с независящим отнагрузки М_{пуск д} – невозможно.

3. М_динд2М_с

Обеспечивает ограничение ускорений можно только путем использования систем ЭП, которые развивают в переходных процессах при разных статических нагрузках различные М_пуск и М_торм. В этом случае ускорение при наложеном тормозе обязательно превысит допустимое a_max>a_доп, обеспечить ограничение ускорения в этом режиме можно путем использования системы непрерывного выравнивания без наложения тормоза, либо с наложением тормоза после окончания процесса точной остановки.

11.Статические нагрузки механизмов ЦБТ. Механический способ регулирования производительности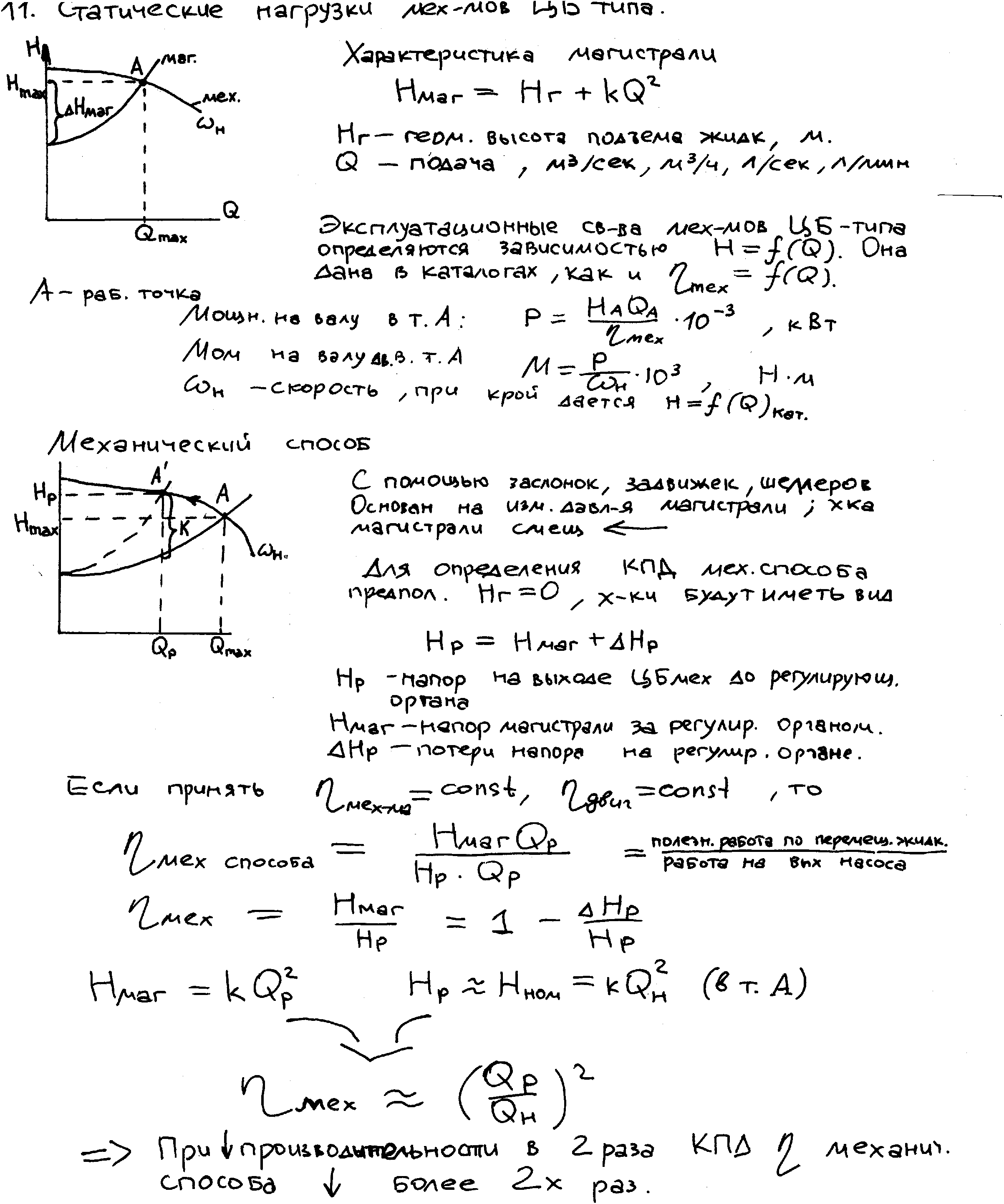

12 Электрический способ регулирования производительности механизмов центробежного типа.

Этот способ является экономичным и обеспечивает возможности автоматизации процесса регулирования.

Эффект изменения производительности и напора достигается за счет уменьшения скорости вращения вала механизма центробежного типа.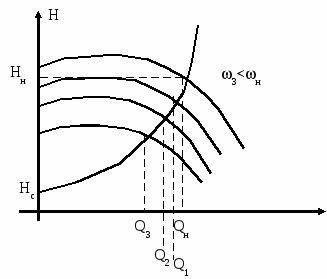



Q


Для расчета характеристик на пониженной скорости применяются законы пропорциональности насоса:







Данные зависимости получены в предположении, что КПД механизма при ₁, ₂ остается постоянным.

Постоянство КПД соблюдается, если статический напор Н_ст=0, это характерно для вентиляторов.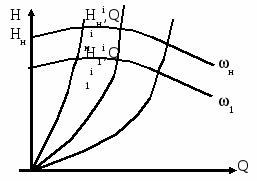







Если статический напор Н_ст0, т.е.

(данная зависимость характерна для насосов). При этом КПД в рабочих точках непостоянный.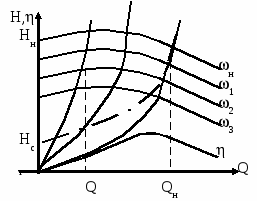



Н_ст0
Для пересчета на пониженную скорость необходимо:

1. 
   Задаться точками на характеристике со скоростью равной =_н.
   

2. 
   Рассчитать параболы для каждой из точек, которые будут являться линиями равного КПД.
   

3. 
   Каждой точке параболы соответствует своя скорость механизма:
   

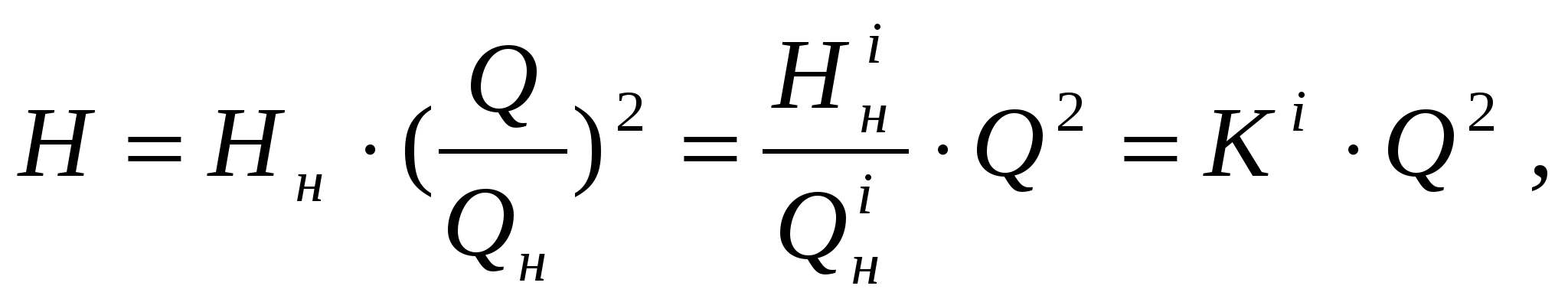
Оглавление

1.Статические нагрузки двухконцевых лебедок 1

2.Методы предварительного выбора типовых ОПМ 2

3.Способы уменьшения механических колебаний 4

4.Выбор зазоров в зубчатых передачах 5

5.Электромеханические колебания резонансного характера 6

6.Схема безопасного спуска для крановых механизмов с ДПТ ПВ 7

7. Требования, предъявляемые к ЭП экскаваторов. ЭП механизма подъема экскаватора с магнитным усилителем 8

8.Оптимальная структура экскаваторного ЭП. Режим К3 10

9.Автоматизация подъемно-транспортных механизмов циклического действия 11

10. Динамика автоматизированных ЭП ПТМ. Определение необходимости регулирования пускового момента 12

11.Статические нагрузки механизмов ЦБТ. Механический способ регулирования производительности 13

12 Электрический способ регулирования производительности механизмов центробежного типа. 14