1. Строение атомного ядра
 Скачать 2.12 Mb.
|
№1. Строение атомного ядра. Атом состоит из ядра и окружающего его электронного "облака". Находящиеся в электронном облаке электроны несут отрицательный электрический заряд. Протоны, входящие в состав ядра, несут положительный заряд. В любом атоме число протонов в ядре в точности равно числу электронов в электронном облаке, поэтому атом в целом – нейтральная частица, не несущая заряда. Атом может потерять один или несколько электронов или наоборот – захватить чужие электроны. В этом случае атом приобретает положительный или отрицательный заряд и называется ионом. Практически вся масса атома сосредоточена в его ядре, Кроме протонов, в состав ядра большинства атомов входят нейтроны, не несущие никакого заряда. Масса нейтрона практически не отличается от массы протона. Вместе протоны и нейтроны называются нуклонами . Электроны, протоны и нейтроны являются главными "строительными деталями" атомов и называются субатомными частицами.
Масштабы физических величин в ядерной физике. 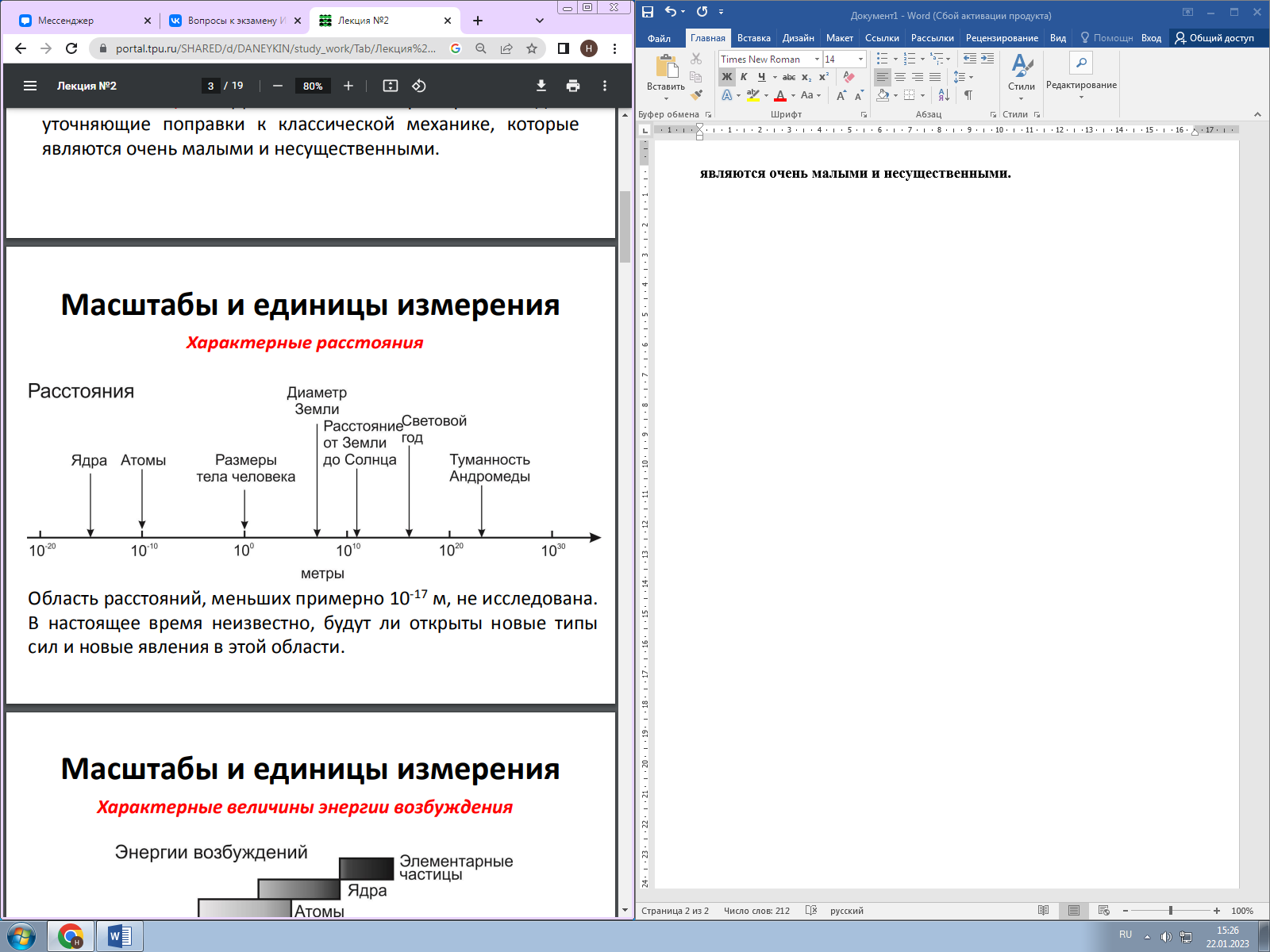 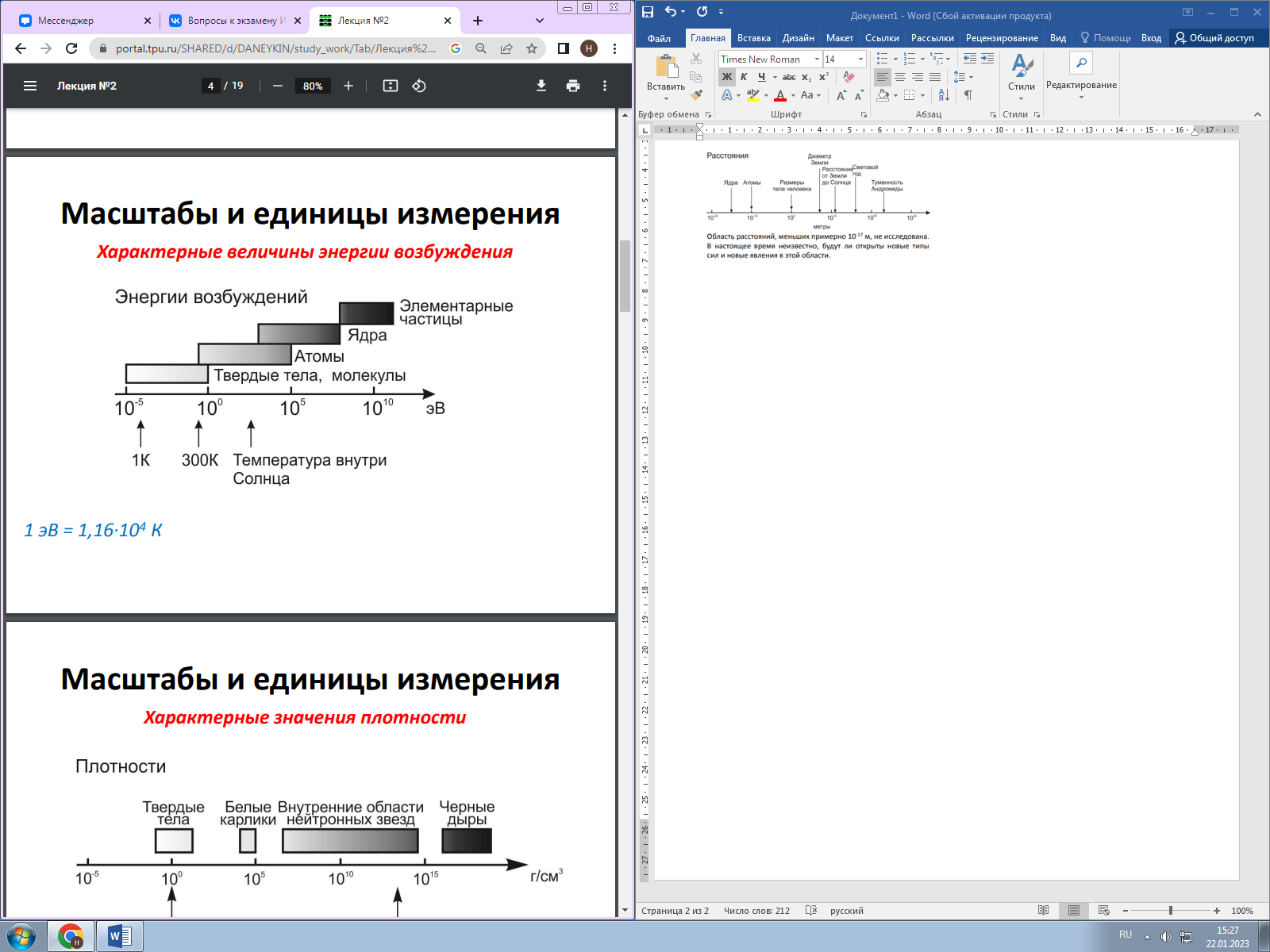      Энергетическая шкала масс, атомная единица массы, дефект масс. А́томная едини́ца ма́ссы — внесистемная единица массы, применяемая для масс молекул, атомов, атомных ядер и элементарных частиц. Атомная единица массы определяется как 1⁄12 массы свободного покоящегося атома углерода 12C, находящегося в основном состоянии. 1 а. е. м. = 1,660 539 066 60(50)⋅10−27 кг.  2. Определение размеров ядер в опытах по рассеянию частиц. Эксперименты Резерфорда, Хофштадтера. Опыт Резерфорда. Используя естественный источник радиоактивного излучения, Резерфорд построил пушку, дававшую направленный и сфокусированный поток частиц. Пушка представляла собой свинцовый ящик с узкой прорезью, внутрь которого был помещен радиоактивный материал. Благодаря этому частицы (в данном случае альфа-частицы, состоящие из двух протонов и двух нейтронов), испускаемые радиоактивным веществом во всех направлениях, кроме одного, поглощались свинцовым экраном, и лишь через прорезь вылетал направленный пучок альфа-частиц. Далее на пути пучка стояло еще несколько свинцовых экранов с узкими прорезями, отсекавших частицы, отклоняющиеся от строго заданного направления. В результате к мишени подлетал идеально сфокусированный пучок альфа-частиц, а сама мишень представляла собой тончайший лист золотой фольги. В нее-то и ударял альфа-луч. После столкновения с атомами фольги альфа-частицы продолжали свой путь и попадали на люминесцентный экран, установленный позади мишени, на котором при попадании на него альфа-частиц регистрировались вспышки. По ним экспериментатор мог судить, в каком количестве и насколько альфа-частицы отклоняются от направления прямолинейного движения в результате столкновений с атомами фольги. 3. Радиоактивность. Радиоактивностью называется способность атомного ядра самопроизвольно распадаться с испусканием частиц. Радиоактивный распад ядра возможен тогда, когда он энергетически выгоден, т.е. сопровождается выделением энергии. Условием этого является превышение массы M исходного ядра суммы масс mi продуктов распада, которому соответствует неравенство M > ∑mi. Это условие является необходимым, но не всегда достаточным. Распад может быть запрещен другими законами сохранения – сохранения момента количества движения, электрического заряда, барионного заряда и т.д. Радиоактивный распад характеризуется временем жизни радиоактивного изотопа, типом испускаемых частиц, их энергиями. Радиоактивный распад – явление вероятностное (статистическое). Если в образце имеется N нераспавшихся ядер, то невозможно указать, какие из них распадутся за бесконечно малый интервал времени dt, т.е. судьба каждого ядра является полностью неопределенной. Можно сказать, что радиоактивные ядра не имеют возраста. Однако полностью определенной является вероятность распада ядра за 1 с, называемая постоянной распада l. Таким образом, предсказуемым является число dN ядер, распавшихся за интервал dt:  (1)На основании формулы (1), представляющей закон радиоактивного распада в дифференциальном виде, возможно определить важнейшую характеристику радионуклида – его активность А:  . (2)Согласно (2) активность определяется как скорость радиоактивного распада. Активность - это количество актов распада (в общем случае актов радиоактивных, ядерных превращений) в единицу времени. Используя (1), можно перейти к интегральному виду закона радиоактивного распада:  , (3)где N0 - число нераспавшихся ядер при t = 0, N – число нераспавшихся ядер по истечении времени t. Формулу (3) используют для определения периода полураспада T1/2 из условия t = T1/2, если N/N0 = 1/2. Подставив это условие в (1.3), получим:  . (4)Величина T1/2 является интегральной характеристикой скорости распада, поскольку определяет время, необходимое для уменьшения активности радионуклида в 2 раза. Период полураспада (T1/2) – время, в течение которого распадается половина наличного числа радиоактивных атомов. Основными видами радиоактивного распада являются: α-распад – испускание атомным ядром α-частицы; β-распад – испускание атомным ядром электрона и антинейтрино, позитрона и нейтрино, поглощение ядром атомного электрона с испусканием нейтрино; γ-распад – испускание атомным ядром γ-квантов; спонтанное деление – распад атомного ядра на два осколка сравнимой массы. Радионукли́ды, радиоакти́вные нукли́ды (менее точно — радиоакти́вные изото́пы, радиоизото́пы) — нуклиды, ядра которых нестабильны и испытывают радиоактивный распад. Большинство известных нуклидов радиоактивны (стабильными являются лишь около 300 из более чем 3000 нуклидов, известных науке). Радиоактивны все нуклиды, имеющие зарядовое число Z, равное 43 (технеций) или 61 (прометий) или большее 82 (свинец); соответствующие элементы называются радиоактивными элементами. Радионуклиды (главным образом бета-неустойчивые) существуют у любого элемента (то есть для любого зарядового числа), причём у любого элемента радионуклидов существенно больше, чем стабильных нуклидов.
№4. Сечение реакции Когда сталкиваются две субатомные частицы (например, α-частица и ядро золота в опыте Резерфорда), между ними может произойти взаимодействие, а может и не произойти. В последнем случае частицы сохраняют неизменными все свои характеристики. Мы не можем предсказать результат столкновения двух конкретных частиц, а лишь вероятность того или иного исхода столкновения. Таким образом, мы оперируем с вероятностями событий. Это вероятностное, а не строго определенное знание (или предсказание) того или иного события отличает физику микромира от физики классических объектов. Основной величиной, которой оперируют физики, исследующие столкновение микрообъектов, является эффективное сечение или просто сечение (более полное название поперечное эффективное сечение). Именно эта величина определяет вероятность того или иного результата столкновения. Результат опыта Резерфорда и, вообще, почти всех экспериментов по столкновению частиц выражается через эту величину. Определим её. Для этого вернемся к опыту Резерфорда. Пусть мишенью является ядро золота, расположенное внутри объема пространства кубической формы с длиной ребра 1 см (рис. 1), и на одну из граней этого кубика под углом 90о в единицу времени (1 с) падает j α-частиц однородно распределенных в пространстве (j – не что иное как плотность потока α-частиц и имеет размерность см-2с-1). Отметим, что других α-частиц помимо тех, которые бомбардируют кубик, нет. В результате взаимодействия с ядром из каждых j частиц N изменит траекторию (рассеется). Поэтому численно вероятность взаимодействия отдельной  -частицы с ядром золота равна N/j. Именно это отношение с учетом его размерности и называют эффективным сечением σ, т. е.
Очевидно σ имеет размерность площади (см2).  Рис. 1. К понятию “эффективное сечение” Происхождение словосочетания “поперечное эффективное сечение” можно пояснить следующим примером. При механическом соударении двух шаров, из которых один покоится внутри единичного кубического объема, а о другом известно лишь то, что он падает нормально на грань этого кубика и имеет размеры незначительные по сравнению с размерами покоящегося шара, вероятность соударения шаров численно равна площади поперечного сечения s покоящегося шара, т.е. σ = s. Для взаимодействий, не являющихся механическими (контактными), σ - эффективная площадь, характеризующая вероятность конкретного процесса. Она может быть как больше геометрической площади (например, кулоновское взаимодействие), так и меньше неё (слабое взаимодействие). Реальная мишень содержит не одно, а большое число ядер. В этом случае число N частиц, испытавших в единицу времени взаимодействие с ядрами и изменивших траекторию (рассеявшихся), при условии однократного взаимодействия каждой частицы (тонкая мишень) дается формулой
где σ – уже определённое нами эффективное сечение рассеяния частицы ядром; n – число ядер мишени в единице объёма (в см-3); S – облучаемая площадь мишени (в см2); l – толщина мишени (в см); M – полное число ядер в облучаемой части мишени. Понятие σ используют как для характеристики вероятности реакции между частицами a + b → c + d, так и для ядерной реакции A + а → B + b, где А и В – начальное и конечное ядра, а – налетающая на ядро А частица, b – появившаяся в результате реакции частица (например, выбитый из ядра А протон). В этом случае N в выражении (2) – число частиц b, вылетающих в единицу времени из мишени во всех направлениях. 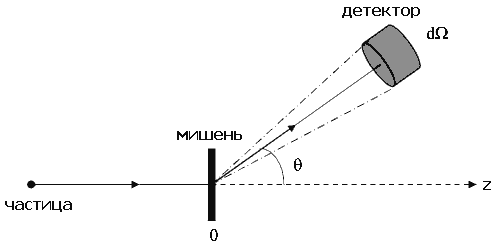 Рис. 2. К понятию “дифференциальное сечение” dσ/dΩ. Случай аксиальной симметрии Если рассматривать частицы, вылетающие в направлении, характеризуемом углами  и  в телесный угол dΩ (θ и φ – полярный и азимутальный углы, а ось z совпадает с направлением движения налетающей частицы), то соотношение (2) записывается в виде
где dN( ,φ) – число частиц, вылетевших под углами и внутри d , или
Величина dσ/dΩ = σ(θ,φ) называется дифференциальным сечением, в отличие от σ – полного сечения:  в случае аксиальной симметрии. В случае кулоновского рассеяния частицы с энергией E и зарядом Z1 на тяжелом точечном рассеивающем центре с зарядом Z2 дифференциальное сечение рассеяния имеет вид
Эта формула была использована Резерфордом для описания упругого рассеяния -частиц на ядрах золота и обычно называется формулой Резерфорда.Если, помимо углов вылета продуктов реакции, определять их энергию, то можно найти вероятность процесса, в котором какой-то из продуктов реакции летит под углами θ и φ внутри телесного угла dΩ и имеет при этом энергию от E до E+dE. Сечение данного процесса обозначают 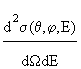 и называют дважды дифференциальным. Очевидно, ещё большая детализация наших знаний о реакции требует использования понятий трижды, четырежды и т. д. дифференциальных сечений. Единица измерения полного сечения σ – 1 барн: 1 барн = 1 б = 10-24 см2 = 100 Фм2, что по порядку величины – поперечная площадь атомного ядра. Дифференциальное эффективное сечение dσ/dΩ измеряют в барн/стерадиан. Закон Бугера-Ламберта-Бера: каждая молекула (ион) растворённого вещества поглощает одинаковую часть монохроматического излучения; интенсивность излучения после прохождения слоя раствора уменьшается экспоненциально с увеличением концентрации растворённого вещества, а оптическая плотность линейно увеличивается с ростом концентрации. Этот закон объединяет два более простых закона: закон Бугера-Ламберта и закон Бера. Закон Бугера-Ламберта: говорит о том, что каждый слой однородного вещества поглощает равную долю падающего на него монохроматического излучения. Закон Бера: устанавливает связь между поглощением и концентрацией: поглощение монохроматического излучения прямо пропорционально концентрации поглощающего вещества. Вывод закона Бугера-Ламберта-Бера: В толще раствора мысленно выделим элементарный слой сечением 1 см2 и толщиной dx см. Объём этого слоя равен dx см3. Если концентрацию раствора выразить через число молекул (ионов) растворённого вещества в 1 см3, то их количество в элементарном слое равно Ndx. Направим на элементарный слой, перпендикулярно к нему поток излучения с длиной волны лямбда и интенсивностью I (интенсивность равна энергии излучения, падающего на единицу поверхности в единицу времени). Предположим, что монохроматическое излучение с длиной волны лямбда поглощается только молекулами растворённого вещества и притом в равных количествах. Тогда уменьшение интенсивности излучения при прохождении через элементарный слой будет пропорционально числу поглощающих молекул и интенсивности падающего излучения: -dI = εNIdx Закон Ламберта справедлив при любой толщине слоя, если свет является монохроматичным, т.е. характеризуется только одной определённом частотой колебаний. Несоблюдение условия монохроматичиности света приводит к нарушению этого закона, так как коэффициент поглощения зависит от длины волны. Область применения закона Бера является значительно более узкой, так как он предполагает независимость коэффициента поглощения от концентрации. Однако в растворах небольших концентрации коэффициент поглощения изменяется с ростом концентрации, так как при этом изменяется состояние вещества в растворе (вследствие ассоциации, диссоциации, полимеризации и т.д.). Спектры излучения и поглощения. Как правило, анализируемая проба излучает и поглощает полихроматический свет, включающий кванты разной энергии и разной длины волны. Однако для аналитика предпочтительнее измерять испускание или поглощение света, в котором все кванты примерно одинаковы по энергии, соответствуют одной длине волны. Чтобы выделить ее из полихроматического излучения, нужно особое устройство – монохроматор. Спектральные приборы, снабженные монохроматорами, называют спектрометрами, спектрографами или стилоскопами, в зависимости от используемого в них приемника излучения, то есть от того, какой способ регистрации спектра (фотоэлектрический, фотографический или визуальный) применяется в этих приборах. С помощью таких приборов можно зарегистрировать спектр излучения или спектр поглощения исследуемой пробы №5. Энергия связи ядра – минимальная энергия, необходимая для того, чтобы разделить ядро на составляющие его нуклоны (протоны и нейтроны). Удельная энергия связи, то есть изменение энергии системы при добавлении одной частицы, называется химическим потенциалом. Для системы, состоящей из нескольких видов частиц существует несколько химических потенциалов по числу видов частиц.  На рис. 1 показана зависимость удельной энергии связи ядра ε от числа нуклонов A. Видно, что наиболее сильно связаны ядра в районе железа и никеля (A 55-60). Такой ход зависимости ε(A) показывает, что для легких ядер энергетически выгодны реакции синтеза более тяжелых ядер, а тяжелых − деление на более легкие осколки. №6. Капельная модель. Формула Вайцзеккера для энергии связи ядер В капельной модели ядро рассматривается как сферическая капля несжимаемой заряженной ядерной жидкости радиуса R = r0A1/3. То есть в энергии связи ядра учитываются объемная, поверхностная и кулоновская энергии. Дополнительно учитываются выходящие за рамки чисто капельных представлений энергия симметрии и энергия спаривания. В рамках этой модели можно получить полуэмпирическую формулу Вайцзеккера для энергии связи ядра. Eсв(A,Z) = a1A - a2A2/3 - a3Z2/A1/3 - a4(A/2 - Z)2/A + a5A-3/4. Первое слагаемое в энергии связи ядра, подобного жидкой капле, пропорционально массовому числу A и описывает примерное постоянство удельной энергии связи ядер. Второе слагаемое - поверхностная энергия ядра уменьшает полную энергию связи, так как нуклоны, находящиеся на поверхности имеют меньше связей, чем частицы внутри ядра. Это аналог поверхностного натяжения. Третье слагаемое в энергии связи обусловлено кулоновским взаимодействием протонов. В капельной модели предполагается, что электрический заряд протонов равномерно распределен внутри сферы радиуса R = r0A1/3. Четвертое слагаемое - энергия симметрии ядра отражает тенденцию к стабильности ядер с N = Z. Пятое слагаемое - энергия спаривания учитывает повышенную стабильность основных состояний ядер с четным числом протонов и/или нейтронов. Входящие в формулу коэффициенты a1, a2, a3, a4 и a5 оцениваются из экспериментальных данных по знергиям связи ядер, что дает a1 = 15.75 МэВ; a2 = 17.8 МэВ; a3 = 0.711 МэВ; a4 = 23.7 МэВ; 
На рисунке показаны экспериментальные значения удельной энергии связи  = Eсв/A и расчет по формуле Вайцзеккера (плавная кривая).Формула Вайцзеккера позволяет по заданным значениям A и Z вычислять энергию связи ядра с погрешностью 10 МэВ. При A  100 это дает относительную ошибку 10-2. Наибольшее расхождение между эспериментально измеренными величинами энергии связи ядра и расчетами по формуле Вайцзеккера наблюдается в области магических чисел. Это объясняется тем, что в капельной модели не учитываются неоднородности распределения ядерной материи, обусловленные оболочечной структурой атомных ядер.№7. – №8- Явление β-распада состоит в том, что ядро(A,Z) самопроизвольно испускает лептоны 1-го поколения – электрон (позитрон) и электронное нейтрино (электронное антинейтрино), переходя в ядро с тем же массовым числом А, но с атомным номером Z, на единицу большим или меньшим. При e-захвате ядро поглощает один из электронов атомной оболочки (обычно из ближайшей к нему K-оболочки), испуская нейтрино.В литературе для e-захвата часто используется термин EC (Electron Capture). Существуют три типа β-распада – β--распад, β+-распад и е-захват.
Главной особенностью β-распада является то, что он обусловлен слабым взаимодействием. Бета-распад - процесс не внутриядерный, а внутринуклонный. В ядре распадается одиночный нуклон. Происходящие при этом внутри ядра превращения нуклонов и энергетические условия β-распада имеют вид (массу нейтрино полагаем нулевой):
№9. Альфа-распад (или α-распад) – самопроизвольное испускание атомными ядрами альфа-частиц (ядер атома гелия). Поскольку α-частица представляет собой связанное состояние двух протонов и двух нейтронов (т.е. ядро гелия), то в результате α-распада конечное ядро содержит на 2 протона и 2 нейтрона меньше, чем начальное. Например, α-распад ядра плутония, содержащего 239 нуклонов, в числе которых 94 протона, записывается следующим образом: 239Pu→ 235U + α. Конечным ядром после распада является ядро урана, содержащее 235 нуклонов, из которых 92 протона. Альфа-распад становится энергетически возможным для ядер, содержащих не менее 60 протонов. Для того чтобы происходил α-распад, необходимо, чтобы масса исходного ядра M(A,Z) была больше суммы масс конечного ядра M(A-4, Z-2) и α-частицы mα: M(A,Z) > M(A-4, Z-2) + mα.  №10. В этой модели ядро рассматривается как сферическая капля несжимаемой заряженной ядерной жидкости радиуса R = r0A1/3. С ее помощью удалось объяснить многие свойства ядра и, в первую очередь, получить полуэмпирическую формулу для энергии связи ядра. Первое (главное) слагаемое в энергии связи ядра, подобного жидкому или твердому телу, должно быть пропорционально массовому числу A:
Этот член представляет объемную энергию ядра и может быть интерпретирован как энергия связи ядра, симметричного по нейтронам и протонам, в пределе больших А и отсутствия кулоновских сил. Ранее уже говорилось, что эксперимент подтверждает примерную пропорциональность энергии связи Eсв массовому числу A. Второй член, который должен быть учтен в рассматриваемой модели, это - поверхностная энергия ядра. Она будет уменьшать полную энергию связи, так как нуклоны, находящиеся на поверхности имеют меньше соседей, чем внутренние частицы. Это хорошо известный эффект поверхностного натяжения. Следует однако заметить, что, в отличии от молекул классических жидкостей, нуклоны на поверхности ядра обладают избыточной не только потенциальной , но и кинетической энергией (это легко показать, например, в модели оболочек). Поверхностная энергия пропорциональна поверхности сферической капли. Следовательно она должна зависеть от массового числа как A2/3:
Третий член в энергии связи обусловлен кулоновским взаимодействием протонов. В капельной модели предполагается, что электрический заряд протонов равномерно распределена внутри сферы радиуса R = r0A1/3. Это создает кулоновскую энергию ядра
Эта энергия также уменьшает общую энергию связи ядра. Капельная модель учитывает вклад в энергию связи ядра объемной, поверхностной и электростатической энергии. Этих слагаемых однако не достаточно для корректного описания энергии связи реальных ядер. Чтобы учесть наблюдаемые в эксперименте тенденции, в энергию связи Eсв необходимо ввести дополнительные члены, которые не могут быть обоснованны в рамках капельной модели ядра. Прежде всего необходимо включить в Eсв энергию симметрии ядра, которая отражает тенденцию к стабильности ядер с N = Z. Энергию симметрии можно разделить на кинетическую и потенциальную части. Кинетическая энергия симметрии была рассмотрена в модели ферми-газа. Как видно из формулы (4), она пропорциональна (A/2 - Z)2/A . Аналогичным образом ведет себя потенциальная энергия симметрии. Эта энергия обусловлена тем, что принцип Паули запрещает вплотную сближаться двум нуклонам одинакового сорта с одинаковыми ориентациями спинов. Вследствие чего взаимодействие нейтрона с протоном в ядре в среднем сильнее, чем взаимодействие между одинаковыми частицами, что также благоприятствует выравниванию числа нейтронов и протонов в ядре. Итак, из энергии связи Eсв надо вычесть энергию симметрии ядра
Наконец, чтобы учесть наблюдаемое в эксперименте скачкообразное изменение энергии связи ядра при добавлении к нему или удалении из него одного нуклона, надо добавить в Eсв парную энергию (энергию разрыва нуклонной пары). Эта энергия апроксимируется выражением
где a5 > 0 для четно-четных ядер, = 0 для нечетных ядер и < 0 для нечетно-нечетных ядер. Окончательное выражение для энергии связи ядра имеет вид
Входящие в него коэффициенты a1, a2, a3, a4 и a5 оцениваются из экспериментальных данных по энергиям связи ядер, что дает a1 = 15.75 МэВ; a2 = 17.8 МэВ; a3 = 0.711 МэВ; a4 = 23.7 МэВ;  Полученное соотношение называется полуэмпирической формулой Вейцзеккера для энергии связи ядра. С ее помощью может быть вычислена удельная энергия связи Eсв/A. Вклад различных членов в формулу для удельной энергии связи показан на рис. 1. Спад этой энергии при малых A объясняется ростом по абсолютной величине отрицательного слагаемого, обусловленного поверхностной энергией: -Wпов/A = -a2A-1/3. С другой стороны постепенное уменьшение удельной энергии связи в области тяжелых ядер вызвано кулоновскими силами, так как слагаемое -Wкул/A = -a3Z2/A4/3 растет по абсолютной величине при увеличении Z. Формула (6) позволяет по известным A и Z вычислять энергию связи ядра с погрешностью 10 МэВ (см. рис.2). При A 100 это дает относительную ошибку 10-2. Точность вычисления массы ядра
еще выше 10-4 (здесь mp - масса протона, mn - масса нейтрона и c - скорость света). Наихудшее согласие с экспериментом формула Вейцзеккера обнаруживает в окрестности магических чисел нуклонов (см. рис.2 и 3). Это указывает на важность учета оболочечных эффектов при вычислении энергии связи ядра.
Важное применение капельная модель нашла в объяснении механизма деления тяжелых ядер. Возможность этого процесса обусловлена тем, что удельная энергия связи Eсв/A начиная с области железа - кобальта уменьшается с ростом массового числа A из-за кулоновского члена формулы Вейцзеккера (см. рис. 2). В результате тяжелому ядру оказывается энергетически выгодно распадаться на более легкие фрагменты. Однако выигрыш в удельной энергии связи только необходимое, но не достаточное условие деления. На самом деле процесс деления определяется конкуренцией двух слагаемых энергии связи Eсв: поверхностной и кулоновской энергий. Если ядро меняет свою форму и из сферического превращается, например, в эллипсоидальное, то объем ядра не меняется, но его поверхность увеличивается. Поэтому поверхностная энергия возрастет по абсолютной величине, так что поверхностные силы будут стремиться вернуть ядро в исходное недеформированное состояние. С другой стороны, кулоновская энергия ядра, наоборот, уменьшится по абсолютной величине из-за увеличения среднего расстояния между протонами и кулоновские силы отталкивания будут стремиться увеличить деформацию ядра. При малых деформациях преобладают силы поверхностного натяжения, при больших - силы кулоновского отталкивания. Таким образом, возникает типичный потенциальный барьер (подобный тому, который имеет место при α-распаде), препятствующий мгновенному делению тяжелых ядер (см. рис. 4). Если не принимать во внимание туннельный эффект, обуславливающий медленный самопроизвольный распад очень тяжелых ядер, то для того чтобы ядро разделилось, ему необходимо передать энергию возбуждения равную или большую высоты потенциального барьера. Необходимая энергия возбуждения уменьшается при переходе к более тяжелым ядрам. Нетрудно понять, что величиной определяющей способность ядра к делению является отношение кулоновской энергии к поверхностной. Как следует из формул (2), (3), это отношение равно a3Z2/(a2A). Так как коэффициенты a2, a3 постоянны для всех ядер, то определяющей величиной, очевидно, является отношение Z2/A. Расчеты показывают, что критическим значением является значение Z2/A ≈ 50. При Z2/A > 50 ядра не могут существовать, так как мгновенно делятся. Для обычного соотношения между протонами и нейтронами в тяжелых ядрах этому значению Z2/A отвечает Z ≈ 115.
Капельная модель предсказывает деление ядра на два одинаковых фрагмента. На практике, при делении тяжелого ядра тепловыми нейтронами (последние необходимы для создания нужного возбуждения ядра), действительно как правило образуются два осколка, но их массы не равны. Случаи симметричного деления составляют менее 1% (см. рис. 5). Наиболее вероятно деление на осколки, один из которых примерно в полтора раза тяжелее другого. Наблюдаемая асимметрия деления может быть объяснена влиянием ядерных нейтронных оболочек: тяжелому ядру энергетически выгоднее делиться так, чтобы число нейтронов в осколке было близко к одному из магических чисел (50 или 82). Коллективный характер движения частиц несжимаемой ядерной жидкости должен приводить к поверхностным колебаниям формы капли (без изменения ее объема). Капельная модель качественно правильно предсказывает некоторые характеристики (спин, четность) низколежащих состояний четно-четных ядер. Однако энергии возбуждения этих состояний не соответствуют частотам колебаний поверхности, вычисленным с помощью полуэмпирической формулы Вейцзеккера. Подводя итоги, можно сказать, что капельная модель дает приблизительно правильное представление о массе и энергии связи ядер, что позволяет исследовать энергетические условия разных мод распада ядра (в частности α- и β-распада), качественно описывает структуру низколежащих уровней четно-четных ядер, дает возможность построить полуколичественную теорию деления тяжелых ядер. Вместе с тем, капельная модель не пригодна для количественного описания спектра возбуждений четно-четных ядер, совершенно не затрагивает такие вопросы как - характеристики основных и возбужденных состояний индивидуальных ядер, структура возбужденных состояний нечетных и нечетно-нечетных ядер, периодическое изменение свойств ядер с изменением массового числа и некоторые другие. Не может объяснить капельная модель и одного из основных свойств деления тяжелых ядер - его асимметрии. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
.
e,
.
