1. Строение атомного ядра
 Скачать 2.12 Mb.
|
№11. Модель Ферми-газаВ модели Ферми-газа (ФГМ) нуклоны в ядре рассматриваются как нерелятивистские фермионы, движущиеся в потенциальной яме. Главным допущением модели является предположение, что линейные размеры ямы гораздо больше нуклонных длин волн:
приближенную величину глубины ядерной потенциальной ямы. Поскольку средняя энергия отделения нуклона  от ядра составляет около 8 МэВ, глубина потенциальной ямы V0 = EF +  (42 - 46) МэВ (cм. рис.6.1).Оценку этой же величины можно получить из других соображений, например из решения задачи о потенциале дейтрона. Таким образом, простая модель Ферми-газа приводит к разумным оценкам глубины потенциальной ядерной ямы.
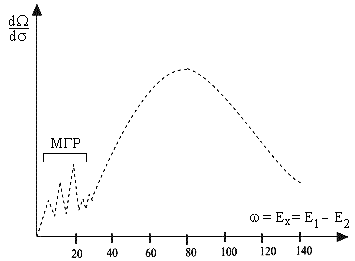
Тот факт, что нуклоны ядра находятся в движении, особенно наглядным образом проявляется в реакциях квазиупругого рассеяния электронов. Сечение этого процесса представляет собой широкий максимум, расположенный выше по энергии, чем область возбуждения мультипольных гигантских резонансов в ядрах (см. рис.6.3). Если бы рассеяние электрона происходило на неподвижном нуклоне, максимум находился бы при переданной ядру энергии, связанной с переданным ядру импульсом q простым нерелятивистским соотношением  = q2/M*, где  =  1 - 2 - переданный импульс, M* - “эффективная” масса нуклона в ядре. Но вместо узкого пика при этой энергии на кривой сечения наблюдается широкий максимум. Его ширина обусловлена именно фермиевским движением нуклонов ядра. Рассеяние электрона происходит – в предельных случаях – как на нуклоне, движущемся навстречу электрону, так и параллельно импульсу электрона. Поэтому измерение ширин пиков квазиупругого рассеяния является способом независимого определения величины импульса Ферми. В табл.1 для нескольких ядер приведены значения импульсов Ферми, рассчитанные из данных по квазиупругому рассеянию электронов.№12. Нуклонная плотность ядер экспериментально определена в опытах по рассеянию электронов промежуточных энергий (Е > 100 МэВ) на ядрах. Дополнили эти эксперименты опыты по рассеянию протонов тех же энергий. Результатом этих опытов было представление о распределении плотности ядерной материи в виде распределения Ферми:
При этом получено, что
Нуклонная плотность ядер, согласно этим измерениям, близка к константе, для средних и тяжелых ядер почти на зависит от А и приближенно составляет  0 0.17 Фм-3.Из (6.9) получим значение импульса Ферми:
№13. Капельная модель. Формула Вайцзеккера для энергии связи ядерВ этой модели ядро рассматривается как сферическая капля несжимаемой заряженной ядерной жидкости радиуса R = r0A1/3. С ее помощью удалось объяснить многие свойства ядра и, в первую очередь, получить полуэмпирическую формулу для энергии связи ядра. Первое (главное) слагаемое в энергии связи ядра, подобного жидкому или твердому телу, должно быть пропорционально массовому числу A:
Этот член представляет объемную энергию ядра и может быть интерпретирован как энергия связи ядра, симметричного по нейтронам и протонам, в пределе больших А и отсутствия кулоновских сил. Ранее уже говорилось, что эксперимент подтверждает примерную пропорциональность энергии связи Eсв массовому числу A. Второй член, который должен быть учтен в рассматриваемой модели, это - поверхностная энергия ядра. Она будет уменьшать полную энергию связи, так как нуклоны, находящиеся на поверхности имеют меньше соседей, чем внутренние частицы. Это хорошо известный эффект поверхностного натяжения. Следует однако заметить, что, в отличии от молекул классических жидкостей, нуклоны на поверхности ядра обладают избыточной не только потенциальной , но и кинетической энергией (это легко показать, например, в модели оболочек). Поверхностная энергия пропорциональна поверхности сферической капли. Следовательно она должна зависеть от массового числа как A2/3:
Третий член в энергии связи обусловлен кулоновским взаимодействием протонов. В капельной модели предполагается, что электрический заряд протонов равномерно распределена внутри сферы радиуса R = r0A1/3. Это создает кулоновскую энергию ядра
Эта энергия также уменьшает общую энергию связи ядра. Капельная модель учитывает вклад в энергию связи ядра объемной, поверхностной и электростатической энергии. Этих слагаемых однако не достаточно для корректного описания энергии связи реальных ядер. Чтобы учесть наблюдаемые в эксперименте тенденции, в энергию связи Eсв необходимо ввести дополнительные члены, которые не могут быть обоснованны в рамках капельной модели ядра. Прежде всего необходимо включить в Eсв энергию симметрии ядра, которая отражает тенденцию к стабильности ядер с N = Z. Энергию симметрии можно разделить на кинетическую и потенциальную части. Кинетическая энергия симметрии была рассмотрена в модели ферми-газа. Как видно из формулы (4), она пропорциональна (A/2 - Z)2/A . Аналогичным образом ведет себя потенциальная энергия симметрии. Эта энергия обусловлена тем, что принцип Паули запрещает вплотную сближаться двум нуклонам одинакового сорта с одинаковыми ориентациями спинов. Вследствие чего взаимодействие нейтрона с протоном в ядре в среднем сильнее, чем взаимодействие между одинаковыми частицами, что также благоприятствует выравниванию числа нейтронов и протонов в ядре. Итак, из энергии связи Eсв надо вычесть энергию симметрии ядра №14. Магические числаСравнение экспериментально измеренных масс атомных ядер с результатами расчетов по формуле Вайцзеккера показывает, что наблюдаются систематические различия между экспериментальными данными и результатами теоретических расчетов, обусловленные оболочечной структурой атомных ядер. Оказалось, что в атомных ядрах также как и в атомах есть оболочки. Ядра, имеющие полностью заполненные оболочки, связаны более сильно по сравнению со своими соседями. Числа нейтронов или протонов, соответствующие заполненным оболочкам, были названы магическими числами. Это числа : 2, 8, 20, 28, 50, 82 и 126. Первые шесть чисел одинаковы для нейтронов и протонов. Число 126 соответствует заполненной нейтронной оболочке. Эти магические числа были получены для ядер вблизи долины стабильности. В том случае, когда число нейтронов N или число протонов Z равно одному из магических чисел, ядро называется магическим. В том случае, когда и N и Z равно магическому числу, ядра являются дважды магическими. Ядра 4He, 16O, 40Ca являются самосопряженными магическими ядрами. Ядро 40Ca - самое тяжелое стабильное ядро с N = Z. После 40Ca все известные ядра с N = Z являются протоноизбыточными и распадаются в результате  +-распада и e-захвата.В настоящее время в связи с повышением точности экспериментов и появлением новых экспериментальных данных наряду с этими магическими числами наблюдают повышенную стабильность ядер с числами нейтронов или протонов N, Z = 14, 40, 64, что соответствует заполнению ядерных подоболочек. Эти числа иногда называют полумагическими. Один из интригующих вопросов современной ядерной физики - следующий: будут ли магические числа справедливыми также и для экзотических ядер, удаленных от долины стабильности? Как проявляются магические числа Прежде, чем ответить на этот вопрос, перечислим какие факты свидетельствуют о проявлении магических чисел. Увеличение энергии связи ядер с заполненными оболочками по сравнению с соседними ядрами. Увеличение энергии отделения одного или двух нуклонов. Наиболее отчетливо этот эффект заметен в энергии отделения двух нейтронов (см. рис. 8.1). Увеличение энергии α-распада для α-радиоактивных ядер вблизи магического числа 126 (рис. 8.1). Увеличение числа β-стабильных изотопов для ядер с магическими числами нейтронов или протонов. В ядрах с заполненными оболочками первый 2+ уровень расположен значительно выше по энергии по сравнению с соседними ядрами (рис. 8.2). Магические числа соответствуют сферическим ядрам, имеющим нулевые значения электрических квадрупольных моментов (см. рис. 8.3). Ядра, с заполненными оболочками, имеют меньшую величину сечения захвата низкоэнергичных нейтронов. |
.
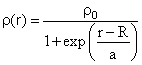(1.25 - 1.35) Фм-1