Тест. 1. технология решения экономических задач с применением финансовых функций excel анализ операций по кредитам и займам
 Скачать 1.4 Mb.
|
Определение будущей стоимости на основе постоянной процентной ставкиЗадача 1. Постановка задачи. На банковский счет под 11,5% годовых внесли 37000 руб. Определить размер вклада по истечении 3 лет, если проценты начисляются каждые полгода. Алгоритм решения задачи. Поскольку необходимо рассчитать единую сумму вклада на основе постоянной процентной ставки, то используем функцию БС (ставка; кпер; плт; пс; тип). Опишем способы задания аргументов данной функции. В связи с тем, что проценты начисляются каждые полгода, аргумент ставка равен 11,5%/2. Общее число периодов начисления равно 3*2 (аргумент кпер). Если решать данную задачу с точки зрения вкладчика, то аргумент пс (начальная стоимость вклада) равный 37 000 руб., задается в виде отрицательной величины (- 37 000), поскольку для вкладчика это отток его денежных средств (вложение средств). Если рассматривать решение данной задачи с точки зрения банка, то данный аргумент (пс) должен быть задан в виде положительной величины, т.к. означает поступление средств в банк. Аргумент плт отсутствует, т.к. вклад не пополняется. Аргумент тип равен 0, т.к. в подобных операциях проценты начисляются в конце каждого периода (задается по умолчанию). Тогда к концу 3-го года на банковском счете имеем: = БС (11,5%/2;3*2;;-37 000) = 51 746,86 руб., с точки зрения вкладчика это доход, = БС (11,5%/2;3*2;;37 000) = - 51 746,86 руб., с точки зрения банка это расход, т.е. возврат денег банком вкладчику. На практике, в зависимости от условий финансовой сделки проценты могут начисляться несколько раз в год, например, ежемесячно, ежеквартально и т.д. Если процент начисляется несколько раз в год, то необходимо определение общего числа периодов начисления процентов и ставки процента за период начисления. В таблице 4.3 приведены данные для наиболее распространенных методов внутригодового учета процентов. Таблица 4.3. Расчет данных для различных вариантов начисления процентов
Этот же расчет можно выполнить по формуле:  (4.1),где: Бс – будущая стоимость (значение) вклада; Пс – текущая стоимость вклада; Кпер – общее число периодов начисления процентов; Ставка – процентная ставка по вкладу за период. Подставив в формулу числовые данные, получим:  Примечания. 1. При аналитических вычислениях в Excel с помощью функций, связанных с аннуитетом, – БЗРАСПИС, БС, ОБЩДОХОД, ОБЩПЛАТ, ОСПЛТ, ПЛТ, ПРПЛТ, ПС, СТАВКА, ЧИСТВНДОХ, ЧИСТНЗ – используется следующее основное уравнение:  (4.2), в котором наименования параметров Пс, Ставка, Кпер, Плт, Бс соответствуют описаниям из таблицы 4.2 (и, соответственно, одноименным встроенным функциям), а параметр Тип определяет обязательность выплаты платежей в начале периода (1) или выплату обычных платежей в конце периода (0). 2. Из уравнения (4.2) могут быть выражены значения бс, пс, ставка, кпер, плт через другие параметры. Эти выражения используются соответствующими функциями Excel. 3. Если ставка равна 0, вместо уравнения (4.2) используется уравнение:  (4.3)4. Если формула (4.1) не предусматривает задание денежных потоков, идущих от клиента, со знаком минус, то в формулах (4.2) и (4.3) это учтено. Нахождение решения задачи 1 по формуле (4.2) дает тот же результат. Иллюстрация решения приведена на рис. 4.1. 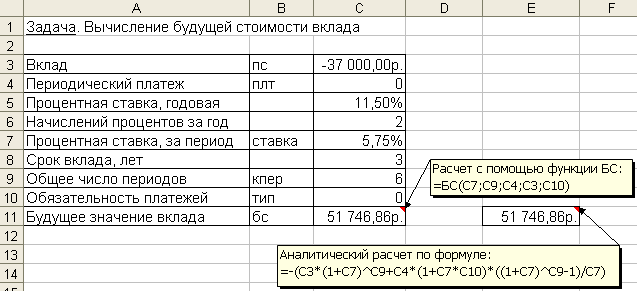 Рис. 4.1. Фрагмент листа Excel с решением задачи о нахождении будущего размера вклада Задача 2. Постановка задачи. Определить, сколько денег окажется на банковском счете, если ежегодно в течение 5 лет под 17% годовых вносится 20 тыс. руб. Взносы осуществляются в начале каждого года. Алгоритм решения задачи. Поскольку следует рассчитать будущую стоимость фиксированных периодических выплат на основе постоянной процентной ставки, то воспользуемся функцией БС со следующими аргументами: = БС(17%;5;-20000;;1) = 164 136,96 руб. Если бы взносы осуществлялись в конце каждого года, результат был бы: = БС(17%;5;-20000) = 140 288 руб. В рассмотренной функции не используется аргумент пс, т.к. первоначально на счете денег не было. Решение задачи может быть найдено с использованием формулы: 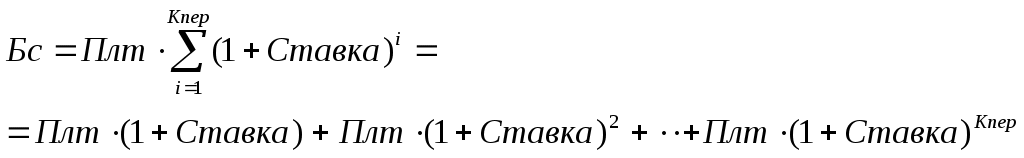 (4.4), где: Бс – будущая стоимость потока фиксированных периодических платежей; Плт – фиксированная периодическая сумма платежа; Кпер – общее число периодов выплат; Ставка – постоянная процентная ставка; i – номер текущего периода выплаты платежа. Результат аналитического вычисления:  Задача 3. Постановка задачи. Достаточно ли положить на счет 85 000 руб. для приобретения через 5 лет легкового автомобиля стоимостью 160 000 руб.? Банк начисляет проценты ежеквартально, годовая ставка 12%. Произвести расчеты при разных вариантах процентной ставки. Алгоритм решения задачи. Поскольку требуется найти будущее значение суммы вклада через 5 лет, для решения поставленной задачи воспользуемся функцией БС. Получим: =БС(12%/4;5*4;;-85000; 0)= 153 519,45р. Как видим, найденная сумма недостаточна для совершения покупки. Чтобы осуществить мечту, существует два варианта: первоначально положить на счет большую сумму или воспользоваться банком, где предусмотрена большая процентная ставка. Внесение дополнительных платежей рассматривать не будем. 1 вариант. Для определения необходимой суммы исходные данные задачи представим в виде таблицы и воспользуемся средством Подбор параметра из меню команды Сервис. Иллюстрация решения представлена на рис. 4.2. 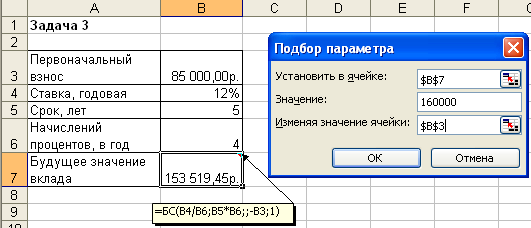 Рис. 4.2. Фрагмент окна Excel с заполненными полями подбора параметров После подтверждения введенных данных в ячейке В7 установится значение 160 000,00р., а в ячейке B3 отобразится результат – 88 588,12р. 2 вариант. В данном случае также можно применить средство Подбор параметра из меню команды Сервис, изменяя ячейку, в которой находится процентная ставка. Однако для анализа влияния процентной ставки на зависящую от нее формулу расчета будущей суммы вклада воспользуемся другим средством – Таблицей подстановки из меню Данные. В дополнение к исходным данным задачи, представленным в виде таблицы, наметим контуры будущей таблицы подстановки: укажем наименования столбцов, в ячейки D9:D16 введем процентные ставки (входы в нашу таблицу подстановки будут размещаться слева в строках), а в ячейку Е8 введем формулу расчета будущего значения единой суммы вклада. Затем выполним необходимые действия по инициализации средства Таблица подстановки и внесения в соответствующее поле подстановки по строкам значения адреса ячейки с процентной ставкой. Иллюстрация окна Excel после задания параметров для таблицы подстановки, а также контрольные значения искомых результатов представлены на рис. 4.3. 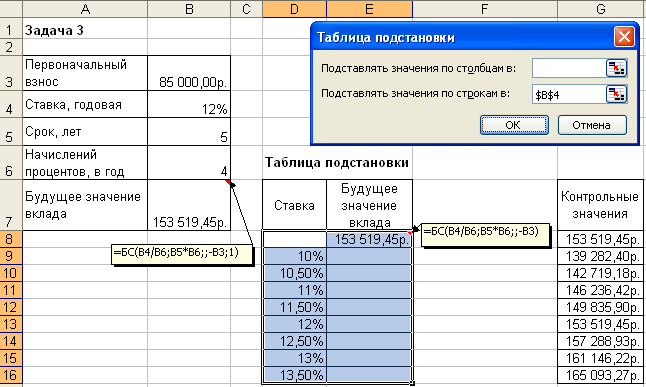 Рис. 4.3. Фрагмент окна Excel с заполненными полями таблицы подстановки После подтверждения в диалоговом окне заданных параметров таблицы подстановки в диапазоне ячеек Е9:Е16 автоматически появятся результаты, полностью совпадающие с контрольными значениями. Из результатов следует, что годовые ставки менее 13% не обеспечивают рост вклада до требуемой величины, равной 160 000 р. При ставке 13% значение вклада вырастет до 161 146,22р., а ставка 13,5% обеспечивает рост вклада до 165 093,27р. Определение будущей стоимости на основе переменной процентной ставки Задача 1. Постановка задачи. По облигации номиналом 50 000 руб., выпущенной на 6 лет, предусмотрен следующий порядок начисления процентов: в первый год – 10%, в следующие два года – 20%, в оставшиеся три года – 25%. Определить будущую стоимость облигации с учетом переменной процентной ставки. Алгоритм решения задачи. Поскольку процентная ставка меняется со временем, но является постоянной на протяжении каждого из периодов одинаковой продолжительности, то для расчета будущего значения инвестиции по сложной процентной ставке следует воспользоваться функцией БЗРАСПИС (первичное; план). И 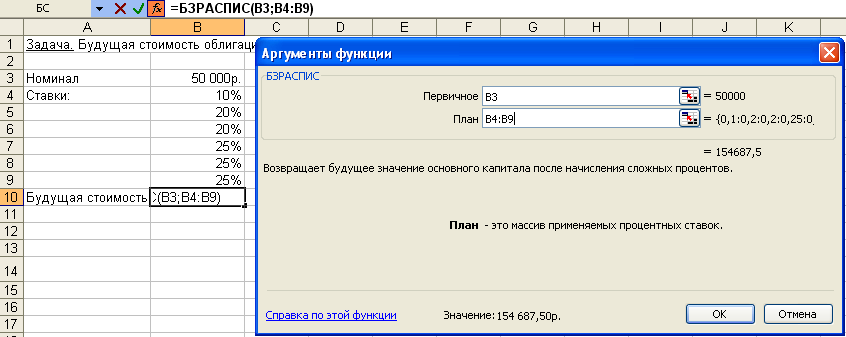 ллюстрация решения задачи представлена на рис. 4.4.Рис. 4.4. Окно функции БЗРАСПИС с данными о будущей стоимости облигации Результат решения задачи – 154 687,50 р. может быть найден и при явной записи функции БЗРАСПИС. Массив процентных ставок в этом случае следует ввести в фигурных скобках: =БЗРАСПИС(50 000; {0,1; 0,2; 0,2; 0,25; 0,25; 0,25}) = 154687,50 Для вычислений будущей стоимости функция БЗРАСПИС использует следующую формулу:  (4.5),где: Бзраспис – будущая стоимость инвестиции при переменной процентной ставке; Пс – текущая стоимость инвестиции; Кпер – общее число периодов; Ставкаi – процентная ставка в i-й период. Расчеты по указанной формуле дают тот же результат:  Задача 2. Постановка задачи. По облигации, выпущенной на 6 лет, предусмотрен порядок начисления процентов, приведенный в задаче 1. Рассчитать номинал облигации, если известно, что ее будущая стоимость составила 154 687,50 руб. Алгоритм решения задачи. Для решения предложенной задачи воспользуемся аппаратом подбора параметра (из меню команды Сервис). П 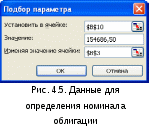 усть исходные данные задачи введены в соответствие с рис. 4.4: в ячейках В4:В9 набраны процентные ставки; ячейка В3 предназначена для хранения значения номинала облигации; в ячейку В10 введена формула =БЗРАСПИС(B3;B4:B9). Инициируем процедуру подбора параметра (из меню команды Сервис) и заполним диалоговое окно в соответствие с данными, представленными на рис. 4.5. После подтверждения ввода данных в результате подбора параметра в ячейке В3 получим значение номинала облигации – 50 000 р. |