Тест. 1. технология решения экономических задач с применением финансовых функций excel анализ операций по кредитам и займам
 Скачать 1.4 Mb. Скачать 1.4 Mb.
|
Задания для самостоятельной работы
2. Определить чистую текущую стоимость проекта, если ставка дисконтирования равна 12%. Проект требует начальных инвестиций в размере 5 млн. руб. Предполагается, что в конце 1 года убыток составит 900 тыс. руб., а в следующие 3 года ожидается доход в размере: 1 500 тыс. руб., 3 200 тыс. руб. и 3 800 тыс. руб. соответственно. Рассчитать также чистую текущую стоимость проекта при условии, что убыток в конце 1 года будет 1 100 тыс. руб. 3. Дать заключение по инвестиционному проекту для 5-ти регионов, если известно, что:
ставка дисконтирования по 1-му региону составляет 5%, по 2-му – 6%, по 3-му – 7%, по 4-му – 8%, по 5-му – 9%. Другие данные о проекте приведены в таблице. Указания. Задачу следует решать, используя средство Таблица подстановки из меню команды Данные. Результаты представить в графическом виде. 4. В инвестиционную компанию для рассмотрения поступили два различных по продолжительности инвестиционных проекта. Предполагаемые данные о проектах приведены в таблице. Необходимо: сравнить проекты и выбрать наиболее эффективный из них; проанализировать проекты при одинаковых объемах инвестируемых средств.
5. Рассматриваются два варианта покупки недвижимости. Первый вариант предполагает единовременную оплату в размере 700 тыс. руб. Второй вариант рассчитан на ежемесячную оплату по 9 тыс. руб. в течение 13 лет. Определить, какой вариант является более выгодным, если ставка процента равна: а) 10% годовых; б) 13% годовых. Рассчитать сумму ежемесячных взносов при ставке 10% годовых, чтобы второй вариант являлся более предпочтительным. 6. Определить текущую стоимость обязательных ежеквартальных платежей размером 80 тыс. руб. в течение 7 лет, если процентная ставка составляет 15% годовых. 7. Рассчитать суммы, которые необходимо положить на депозит для того, чтобы через 6 лет получить 10 млн. руб. при различных вариантах начисления процентов: ежемесячном, ежеквартальном, полугодовом и годовом. Процентная ставка – 11% годовых. 8. Предприниматель получил в банке кредит под 12% годовых. Какова текущая стоимость кредита, если предприниматель должен в течение 7 лет перечислять в банк по 253 000 руб. ежегодно? 9. Рассчитать чистую текущую стоимость проекта, если: к концу первого года его инвестиции составят 34 тыс. руб., а ожидаемые доходы в последующие годы соответственно будут: 5 тыс. руб., 17 тыс. руб. и 25 тыс. руб.; годовая учетная ставка – 12%; решить задачу с теми же условиями, но с учетом предварительной инвестиции в проект 10 тыс. руб.; проанализировать получаемую чистую текущую стоимость проекта при различных первоначальных объемах инвестиций и разных процентных ставках. 10. Для приобретения квартиры молодая семья планирует в дополнение к собственным накоплениям в размере $12 000 взять в банке ипотечный кредит сроком на 20 лет под 11,5% годовых. Ежемесячно семья может выплачивать по кредиту не более $700. На какой кредит может рассчитывать семья? Какой может быть стоимость приобретаемой квартиры? Какой может быть стоимость приобретаемой квартиры, если взять в банке кредит с другими условиями: а) на 10 лет под 10,5% годовых; б) на 15 лет под 11% годовых? Используя команду Таблица подстановки, рассчитать возможную стоимость приобретаемой квартиры: а) при различных размерах собственных накоплений и разных сроках действия кредита; б) при различных ежемесячных платежах по кредиту и разных сроках его действия. 11. У Вас на депозитном счету 10 570,5 рублей, положенные под 1% ежемесячно. Счет открыт 12 месяцев назад. Каков был начальный вклад? 12. Ежегодная плата за приобретенную недвижимость на следующие 25 лет составляет 25 000 рублей. Если считать покупку недвижимости займом с 8% годовых, то какой должна быть его величина, чтобы рассчитаться с займом через 25 лет? 13. Если использовать учетную ставку 0,75% в месяц, сколько необходимо выплатить вначале за имущество, которое по оценке будет стоить 5 000 000 рублей? Ежемесячная плата составляет 25 000 рублей в течение пяти лет. 14. Вы можете позволить себе ежемесячные выплаты 2 500 рублей со ставкой 0,45% (в месяц) в течение 20 лет. Сколько можно занять, чтобы полностью погасить заем? Определение срока платежа и процентной ставкиВ ходе решения задач, связанных с аннуитетом, общее количество периодов выплаты определяется с помощью функции КПЕР (ставка; плт; пс; бс; тип). Процентная ставка за период вычисляется с применением функции СТАВКА (кпер; плт; пс; бс; тип; предположение). Задача 1. Постановка задачи. Рассчитать, через сколько лет вклад размером 100 000 руб. достигнет 1 000 000 руб., если годовая процентная ставка по вкладу 13,5% годовых и начисление процентов производится ежеквартально. Алгоритм решения задачи. При квартальном начислении процентов ставка процента за период начисления равна 13%/4. Чтобы определить общее число периодов выплат для единой суммы вклада, воспользуемся функцией КПЕР со следующими аргументами: ставка = 13%/4; пс = -1; бс = 10. Нули в текущей и будущей суммах можно не набирать, достаточно сохранить между ними пропорции. Значением функции КПЕР является число периодов, необходимое для проведения операции, в данном случае - число кварталов. Для нахождения числа лет полученный результат разделим на 4: = КПЕР (13%/4;;-1;10) / 4 = 18 Иллюстрация решения задачи приведена на рис. 4.11. Для решения задачи можно также воспользоваться формулой (4.1), в которой аргумент Кпер и есть значение функции КПЕР. Выполнив преобразования и прологарифмировав обе части уравнения (4.1), получим: 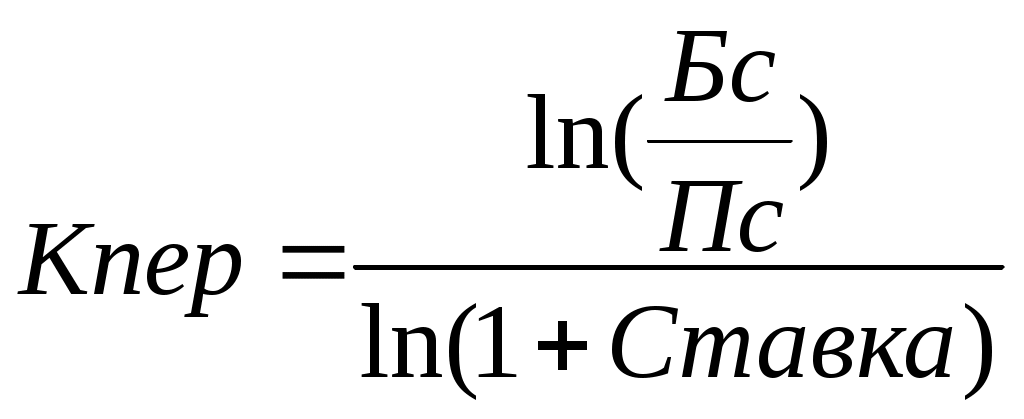 (4.12) (4.12)Подставив в (4.12) значения, убедимся в совпадении результатов: 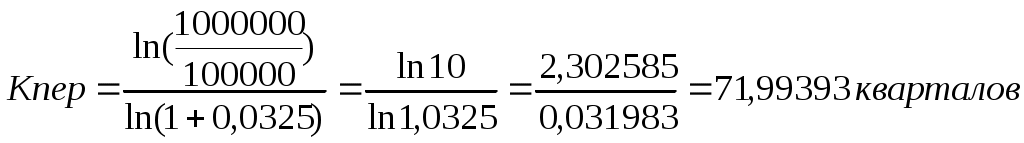 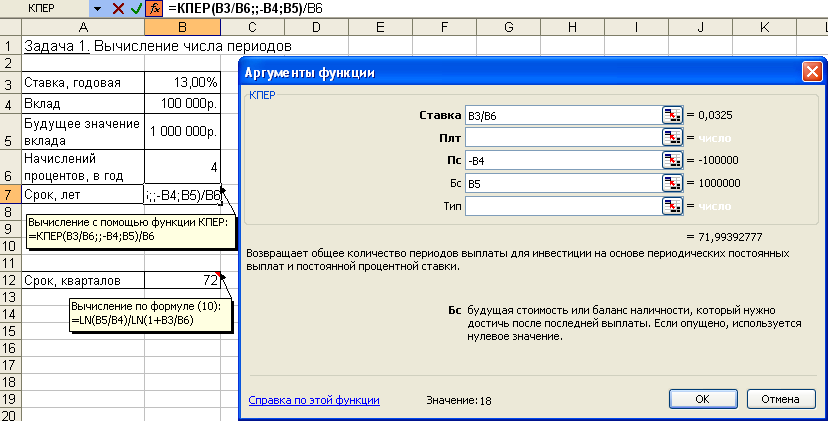 Рис. 4.11. Иллюстрация применения функции КПЕР и аналитической формулы для вычисления числа периодов Задача 2. Постановка задачи. Для покрытия будущих расходов фирма создает фонд. Средства в фонд поступают в виде постоянной годовой ренты постнумерандо. Сумма разового платежа 16 000 руб. На поступившие взносы начисляются 11,2% годовых. Необходимо определить, когда величина фонда будет равна 100 000 руб. Алгоритм решения задачи. Для определения общего числа периодов, через которое будет достигнута нужная сумма, воспользуемся функцией КПЕР с аргументами: ставка = 11,2%; плт = -16; бс = 100. В результате вычислений получим, что через 5 лет величина фонда достигнет отметки 100 000 руб.: = КПЕР (11,2%;-16;;100) = 5 Решение задачи может быть найдено и иным способом – с помощью функций БС (либо ПС) и последующего подбора параметра. Иллюстрация решения приведена на рис. 4.12. 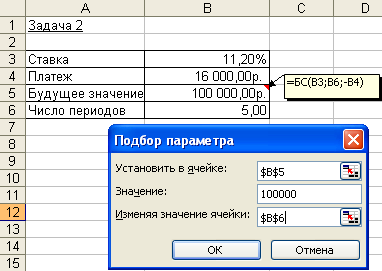 Рис. 4.12. Применение функции БС и механизма подбора параметра для определения числа периодов Задача 3. Постановка задачи. Предположим, что для получения через 2 года суммы в 1 млн. руб. предприятие готово вложить 250 тыс. руб. сразу и затем каждый месяц по 25 тыс. руб. Определить годовую процентную ставку. Алгоритм решения задачи. В данной задаче сумма в 1 млн. руб. формируется за счет приведения к будущему моменту времени начального вклада 250 тыс. руб. и фиксированных ежемесячных выплат. Определим значение процентной ставки за месяц с помощью функции СТАВКА, имеющей аргументы: Кпер = 2*12 = 24 (месяца); Плт = -25; Пс = -250; Бс = 1000. Тогда: = СТАВКА (24;-25;-250;1000) = 1,05% Для вычисления годовой процентной ставки значение, выданное функцией СТАВКА, следует умножить на 12: 1,05%*12 = 12,63%. Процент на вклад должен быть не меньше этой величины. Иллюстрация применения функции СТАВКА в выражениях формулы приведена на рис. 4.13. Обратим внимание, что функция СТАВКА вычисляется методом последовательного приближения и может не иметь решения или иметь несколько решений. 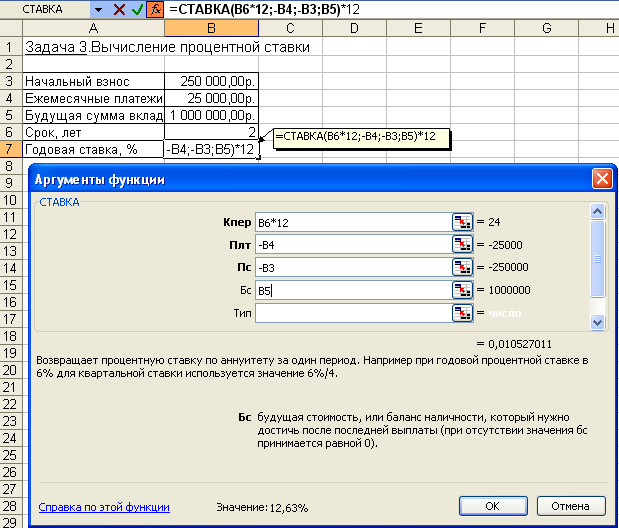 Рис. 4.13. Фрагмент экрана при использовании функции СТАВКА Сначала рассчитывается текущий объем инвестиции при ставке, задаваемой аргументом функции СТАВКА предположение, по умолчанию равным 10%. Если результат получается больше 0, то значение процентной ставки увеличивается, и расчет текущего объема инвестиции повторяется. Если результат оказывается меньше 0, то для следующего приближения значение процентной ставки уменьшается. Процесс завершается, когда решение получится с точностью до 0,0000001 или когда количество итераций превысит 20. В последнем случае считается, что решения нет (формируется ошибка #ЧИСЛО!), и для повторного поиска решения следует изменить значение аргумента предположение (рис. 4.14). Это можно сделать, доб 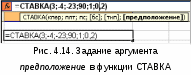 авив его значение из интервала между 0 и 1 в строке формул или, сдвинув ползунок в панели функции СТАВКА, в появившейся строке ввести новое значение аргумента предположение. авив его значение из интервала между 0 и 1 в строке формул или, сдвинув ползунок в панели функции СТАВКА, в появившейся строке ввести новое значение аргумента предположение.Примечания. 1. Следует помнить, что результатами функций КПЕР и СТАВКА являются число периодов и периодическая процентная ставка текущей операции, поэтому для годовых результатов требуются преобразования. 2. Следует также помнить, что для получения корректного результата при работе с функциями КПЕР и СТАВКА, аргументы Бс и Пс должны иметь противоположные знаки. Данное требование вытекает из экономического смысла подобных операций. Задания для самостоятельной работы1. Ссуда размером 58 000 руб., выданная под 12% годовых, погашается ежеквартальными платежами по 6 200 руб. Рассчитайте срок погашения ссуды. 2. Предполагается, что ежегодные доходы от реализации проекта составят 30 млн. руб. Рассчитать срок окупаемости проекта, если затраты по проекту к началу поступления доходов составят 70 млн. руб., а норма дисконтирования – 11,3%. 3. Вычислите, через сколько лет ежемесячные взносы в сумме 15 000 руб. принесут доход в 500 000 руб. при ставке процента 11,9% годовых. 4. Какой вариант инвестиций из трех предпочтительнее по сроку окупаемости? Варианты инвестиций характеризуются потоками платежей, приведенными в таблице (в тыс. руб.).
5. Пусть в долг на 3,5 года дана сумма 1 000 тыс. руб. с условием возврата 1500 тыс. руб. Определить, под какой процент годовых одолжена сумма? 6. Выдан кредит 500 тыс. руб. на 2,5 года. Проценты начисляются раз в полгода. Определить величину процентной ставки за период, если известно, что возврат составит 700 тыс. руб. 7. Вычислить процентную ставку для трехлетнего займа размером 3 млн. руб. с ежеквартальным погашением по 300 тыс. руб. 8. Клиент внес в банк 10 000 руб. и к концу года рассчитывает на 15 000 руб. Проценты начисляются ежемесячно. Определить процентную ставку по вкладу. 9. Кредит в 750 тыс. руб. предоставлен под 12% годовых и предусматривает ежемесячные платежи в размере 8632,5 руб. Определить срок погашения кредита. 10. Ваш остаток на счете пять лет назад составлял 25 000 рублей. В конце каждого года Вы добавляли 4500 рублей. Сегодня баланс равен 70 000 рублей. Какой была Ваша среднегодовая ставка? 11. Имущество с текущей стоимостью 2 000 000 рублей продается в кредит с обязательством погашения кредита в течение пяти лет. Покупатель оплатил 1 850 000 рублей. Не принимая во внимание рост стоимости имущества, определите начальную ставку? 12. Вы заплатили 1 500 000 рублей за имущество, внося ежемесячно по 15 000 рублей. Если Вы продадите имущество через пять лет за 1 900 000 рублей, какой процент сможете получить? 13. Соглашение о потребительском займе предоставляет Вам кредит 10 000 рублей с оплатой 2 000 рублей в месяц в течение 12 месяцев. Какова его процентная ставка? Расчет эффективной и номинальной ставки процентовЧасто на практике возникает необходимость сравнения условий финансовых операций, предусматривающих различные периоды начисления процентов. В этом случае осуществляют приведение соответствующих процентных ставок к их годовому эквиваленту. Реальная доходность финансового контракта с начислением сложных процентов несколько раз в год измеряется эффективной процентной ставкой, которая показывает, какой относительный доход был бы получен за год от начисления процентов. Зная эффективную процентную ставку, можно определить величину соответствующей ей годовой номинальной процентной ставки. Для расчетов указанных величин используются функции – НОМИНАЛ (эффективная_ставка; кол_пер) и ЭФФЕКТ (номинальная_ставка; кол_пер). Задача 1. Постановка задачи. Определить эффективную процентную ставку, если номинальная ставка составляет 9%, а проценты начисляются: а) раз в полгода; б) поквартально; в) ежемесячно. Алгоритм решения задачи. Для определения эффективной процентной ставки воспользуемся функцией ЭФФЕКТ. Непосредственный ввод аргументов дает следующие значения:
Расчет эффективной ставки выполняется по формуле: где Кол_пер – количество периодов в году, за которые начисляются сложные проценты. Выполнив расчет по формуле (4.13), получим тот же результат. В качестве примера приведем вычисления для варианта б). Иллюстрация решения с помощью панели функции приведена на рис. 4.15. 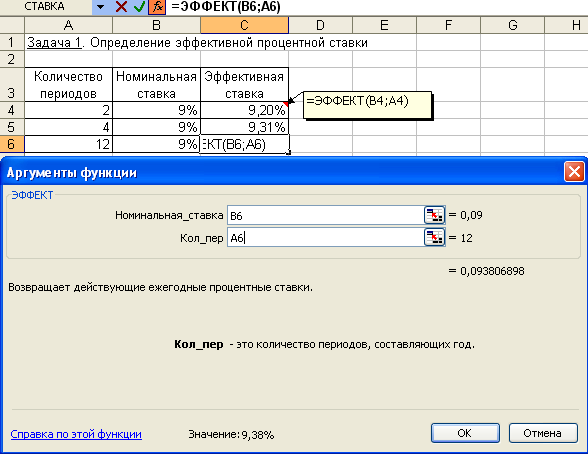 Рис. 4.15. Фрагмент окна при использовании функции ЭФФЕКТ Примечания. 1. Если Номинальная_ставка ≤ 0 или если Кол_пер < 1, то функция ЭФФЕКТ возвращает значение ошибки #ЧИСЛО! 2. Если функция недоступна или возвращает ошибку #ИМЯ?, следует загрузить надстройку «Пакет анализа». Задача 2. Постановка задачи. Известно, что эффективная ставка составляет 16%, начисления производятся ежемесячно. Определить номинальную ставку. Алгоритм решения задачи. Для определения номинальной годовой процентной ставки воспользуемся функцией НОМИНАЛ: = НОМИНАЛ (16%; 12) = 14,93%. Значение функции НОМИНАЛ – это аргумент Номинальная_ставка в формуле (4.13). Задания для самостоятельной работы1. Определить эффективную ставку, если номинальная ставка 10% и начисления процентов осуществляются:
2. Эффективная ставка составляет 12%. Проценты начисляются ежеквартально. Определить номинальную ставку. 3. Ставка банка по срочным валютным депозитам составляет 20% годовых. Какова реальная доходность вклада, если проценты выплачиваются: а) ежемесячно; б) раз в год. Расчет периодических платежей, связанных с погашением займовСреди финансовых функций Excel выделяются функции, связанные с периодическими выплатами: ПЛТ (ставка; кпер; пс; бс; тип) ПРПЛТ (ставка; период; кпер; пс; бс; тип) ОБЩПЛАТ (ставка; кол_пер; нз; нач_период; кон_период; тип) ОСПЛТ (ставка; период; кпер; пс; бс; тип) ОБЩДОХОД (ставка; кол_пер; нз; нач_период; кон_период; тип) Задача 1. Постановка задачи. Клиенту банка необходимо накопить 200 тыс. руб. за 2 года. Клиент обязуется вносить в начале каждого месяца постоянную сумму под 9% годовых. Какой должна быть эта сумма? Алгоритм решения задачи. Для определения ежемесячных выплат применяется функция ПЛТ с аргументами: Ставка = 9%/12 (ставка процента за месяц); Кпер = 2*12 = 24 (общее число месяцев начисления процентов); Бс = 200 (будущая стоимость вклада); Тип = 1, так как вклады пренумерандо. Тогда величина ежемесячных выплат равна: = ПЛТ (9%/12; 24; ; 200; 1) = - 7,58 тыс. руб. Результат со знаком «минус», так как 7,58 тыс. руб. клиент ежемесячно вносит в банк. Иллюстрация решения задачи приведена на рис. 4.16. 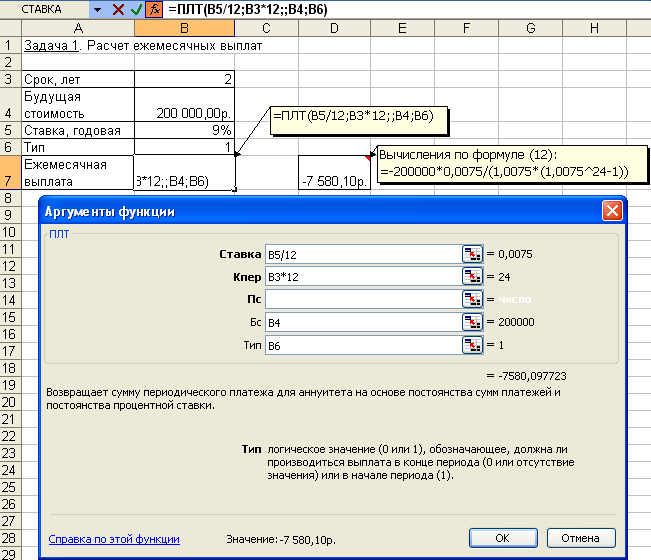 Рис. 4.16. Иллюстрация применения функции ПЛТ Выплаты, определяемые функцией ПЛТ, включают основные платежи и платежи по процентам. Расчет выполняется по формуле, определяемой из (4.2): Расчет задачи по формуле (4.12) дает тот же результат: Задача 2. Постановка задачи. Клиент банка осуществляет заем в размере 5000 руб. под 6% годовых на 6 месяцев. Определить ежемесячные платежи клиента. Платежи осуществляются в конце месяца. Алгоритм решения задачи. Для определения ежемесячных платежей клиента воспользуемся функцией ПЛТ, а также выполним расчет по формуле (4.14): = ПЛТ (6%/12; 6; -5000) = 847,98 руб. Отметим, что для банка выданный кредит – это отрицательная величина, а рассчитанные ежемесячные поступления от клиента – положительная величина. Задача 3. Постановка задачи. Определить платежи по процентам за первый месяц от трехгодичного займа в 100 000 руб. из расчета 10% годовых. Алгоритм решения задачи. Для определения платежа по процентам за первый месяц заданного периода применим функцию ПРПЛТ со следующими аргументами: Ставка = 10%/12 (процентная ставка за месяц); Период = 1 (месяц); Кпер = 3*12 = 36 (месяцев), Пс = 100 000 (величина займа). Тогда платежи по процентам за первый месяц составят: = ПРПЛТ (10%/12; 1; 36; 100000) = - 833,33 руб. Знак «минус» означает, что платеж по процентам необходимо внести. Иллюстрация решения задачи приведена на рис. 4.17. 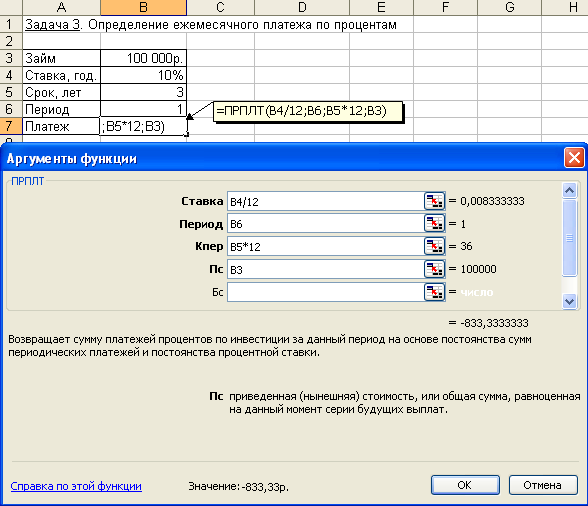 Рис. 4.17. Фрагмент окна с использованием функции ПРПЛТ Задача 4. Постановка задачи. Клиент ежегодно в течение 5 лет вносил деньги на свой счет в банке и накопил 40 000 руб. Определить, какой доход получил клиент банка за последний год, если годовая ставка составила 13,5%. Алгоритм решения задачи. Доход за последний пятый год представляет собой сумму процентов, начисленных на накопленную сумму вложений. Для расчета воспользуемся функцией ПРПЛТ: = ПРПЛТ(13,5%; 5; 5; ; 40000) = 4030,77 руб. Заметим, что при решении данной задачи значения аргументов функции ПРПЛТ Бс и Тип не указываются (считаются равными 0). Задача 5. Постановка задачи. Определить значение основного платежа для первого месяца двухгодичного займа в 60000 руб. под 12% годовых. Алгоритм решения задачи. Сумма основного платежа по займу вычисляется с помощью функции ОСПЛТ: = ОСПЛТ (12%/12; 1; 24; 60000) = - -2 224,41руб. Иллюстрация решения показана на рис. 4.18. 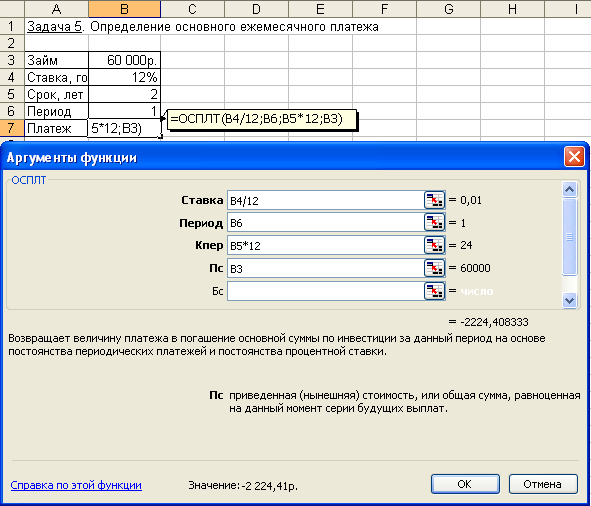 Рис. 4.18. Фрагмент окна с использованием функции ОСПЛТ Знак «минус» в результате означает, что сумму основного долга по займу необходимо внести. Отметим, что сумма выплаты по процентам, вычисляемая с помощью функции ПРПЛТ, и сумма основной выплаты за период, рассчитанная с помощью функции ОСПЛТ, равны полной величине выплаты, вычисляемой с помощью функции ПЛТ. Например, для ранее приведенной задачи 2 ежемесячная выплата клиента составляет: = ПЛТ (6%/12; 6; -5000) = 847,98 руб. Размер основного платежа: = ОСПЛТ (6%/12; 1; 6; -5000) = 822,98 руб. Размер платежа по процентам: = ПРПЛТ (6%/12; 1; 6; -5000) = 25,00 руб. Задача 6. Постановка задачи. Организация взяла ссуду в банке в размере 500 тыс. руб. на 10 лет под 10,5% годовых; проценты начисляются ежемесячно. Определить сумму выплат по процентам за первый месяц и за третий год периода. Алгоритм решения задачи. Для вычисления суммы платежей по процентам за требуемые периоды воспользуемся функцией ОБЩПЛАТ (рис. 4.19). Аргументы функции: Кол_пер = 10*12 = 120 месяцев (общее число выплат); Ставка = 10,5%/12 (процентная ставка за месяц); Нз = 500000 (заем); Тип = 0; для выплаты процентов за 1-й месяц Нач_период = 1 и Кон_период = 1, для выплаты процентов за 3-й год Нач_период = 25 и Кон_период = 36. Выплата за первый месяц составит: = ОБЩПЛАТ(10,5%/12; 120; 500; 1; 1; 0) = - 4,375 тыс. руб. Сумма выплат по процентам за третий год периода составит: = ОБЩПЛАТ (10,5%/12; 120; 500; 25; 36; 0) = - 44,143 тыс. руб. 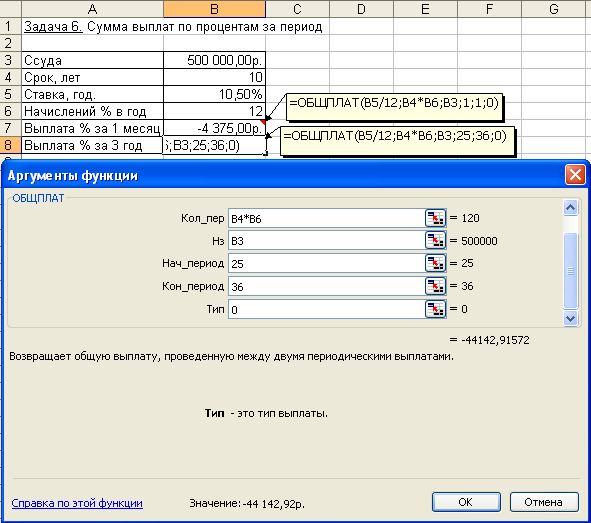 Рис. 4.19. Фрагмент окна с использованием функции ОБЩПЛАТ Задача 7. Постановка задачи. Ссуда размером 1 млн. руб. выдана под 13% годовых сроком на 3 года; проценты начисляются ежеквартально. Определить величину общих выплат по займу за второй год. Алгоритм решения задачи. Предположим, что ссуда погашается равными платежами в конце каждого расчетного периода. Тогда для расчета суммы выплаты задолженности за второй год применим функцию ОБЩДОХОД. Аргументы функции: Кол_пер = 3*4 = 12 кварталов (общее число расчетных периодов); Ставка = 13%/4 (процентная ставка за расчетный период – квартал); Нз = 1000000; Нач_период = 5 и Кон_период = 8 (второй год платежа по ссуде – это период с 5 по 8 квартал); Тип = 0. = ОБЩДОХОД (13%/4; 12; 1000000; 5; 8; 0) = - 331522,23 руб. Иллюстрация решения задачи представлена на рис. 4.20. 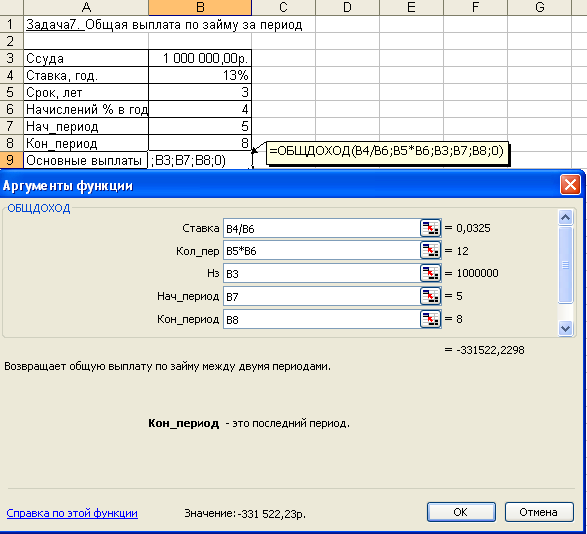 Рис. 4.20. Фрагмент окна с использованием функции ОБЩДОХОД Задача 8. Постановка задачи. Банком выдан кредит в 500 тыс. руб. под 10% годовых сроком на 3 года. Кредит должен быть погашен равными долями, выплачиваемыми в конце каждого года. Разработать план погашения кредита, представив его в виде следующей таблицы:
Алгоритм решения задачи. Введем исходные данные задачи в ячейки электронной таблицы и определим структуру таблицы плана погашения кредита. Расчет числовых значений выполним с помощью функций Excel. Для получения возможности автозаполнения (копирования) формул, введенных для первого периода плана, на другие периоды, укажем абсолютные ссылки на исходные данные. Иллюстрация решения задачи с указанием примечаний со значениями формул вычислений для 3-го периода приведена на рис. 4.21. 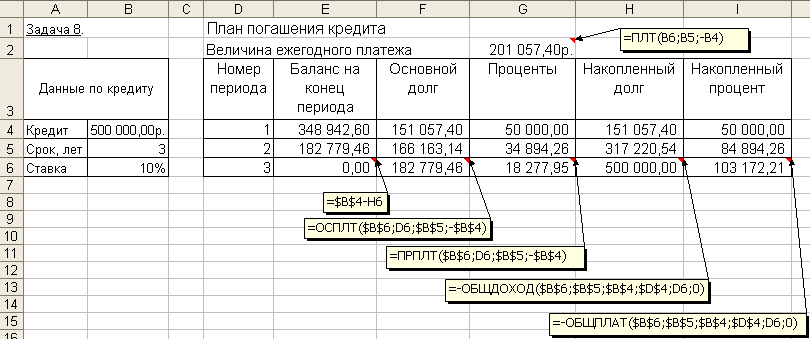 Рис. 4.21. Фрагмент окна с таблицей плана погашения кредита Приведем также формулы с непосредственным заданием значений аргументов при вычислении плановых данных для 1-го периода: размер ежегодного платежа: = ПЛТ (0,1; 3; -500000) = 201 057,40 руб.; основной долг: =ОСПЛТ (0,1;1;3;-500000) = 151 057,40 руб.; проценты: =ПРПЛТ (0,1; 1; 3; -500000) = ;50 000 руб.; накопленный долг: =-ОБЩДОХОД (0,1; 3; 500000; 1; 1; 0) = 151 057,40 руб.; накопленный процент: =-ОБЩПЛАТ (0,1; 3; 500000; 1; 1; 0) = 50 000 руб.; баланс на конец периода: = Кредит – Накопленный долг = 348 942,60 руб. Задача 9. Постановка задачи. В целях покупки недвижимости инвестор взял в банке кредит в сумме 12 млн. руб. Определить ежемесячные выплаты по кредиту для разных процентных ставок и сроков погашения кредита. Алгоритм решения задачи. Ежемесячные выплаты по займу рассчитываются с использованием функции ПЛТ. Однако аргументы данной функции – процентная ставка и срок погашения кредита – по условию могут принимать различные значения. Поэтому рассмотрим влияние этих параметров на заданную функцию. Воспользуемся механизмом Таблица подстановки из меню команды Данные. Выполним следующую последовательность действий. 1. В ячейку электронного листа С3 введем числовое значение суммы кредита (12 000 000). 2. В ячейки С4, С5 введем произвольные (условные) значения процентной ставки (например, 5%) и срока погашения кредита в годах (например, 1), которые нам понадобятся при построении Таблицы подстановки. 3. В ячейки В9:В22 введем различные значения процентных ставок. В ячейки С9:К9 возможные сроки погашения. 4. В ячейку В9 введем формулу для расчета ежемесячных выплат по займу: = ПЛТ (5%/12; 1*12; 12 000 000). Заметим, что в качестве аргументов функции можно вводить как адреса ячеек, так и конкретные исходные значения. 5. Выделим интервал для таблицы данных, включающий формулу и все исходные данные, В9:К22. 6. Выберем команды Данные → Таблица подстановки. В появившемся диалоговом окне (рис. 4.22) заполним соответствующие поля. Поскольку наша таблица зависит от двух параметров, то в поле «Подставлять значения по столбцам в:» введем ссылку на ячейку С5 (срок погашения), а в поле «Подставлять значения по строкам в:» ссылку на ячейку С4 (ставка). 7 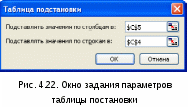 . Подтвердим ввод нажатием клавиши [Enter] или кнопкой ОК. . Подтвердим ввод нажатием клавиши [Enter] или кнопкой ОК. Таблица ежемесячных выплат по кредиту с помощью таблицы подстановки будет сформирована (рис. 4.23). Задания для самостоятельной работы1. Разработайте план погашения кредита, полученного на следующих условиях: а) 700 тыс. руб. сроком на 6 лет под 9% годовых при выплате один раз в конце года. б) 900 тыс. руб. сроком на 9 лет под 7% годовых при выплате один раз в квартал. в) 500 тыс. руб. сроком на 4 лет под 11% годовых при выплате один раз в месяц. 2. Ипотечный кредит размером 2 200 000 руб. предоставлен по ставке 12% годовых сроком на 30 лет и требует ежемесячных платежей. Каков будет остаток основной суммы через 8 лет? 3. Кредит в сумме 5 000 000 руб. предоставлен под 20% годовых сроком на 10 лет. Рассчитать величину остатка основной суммы без учета выплаченных процентов на начало третьего года. 4. Рассчитать сумму процентов, начисленных на вклад в 750 тыс. руб. за 2 года, если банк начисляет проценты ежеквартально из расчета 28% годовых. Какова должна быть годовая депозитная ставка при прочих равных условиях, если за 2 года необходимо удвоить первоначальный вклад? 5. Потребитель получает заем на покупку автомобиля 20 000$ под 8% годовых сроком на три года при ежемесячных выплатах. Какова будет сумма по процентам и основной платеж за первый и последний месяцы выплат? 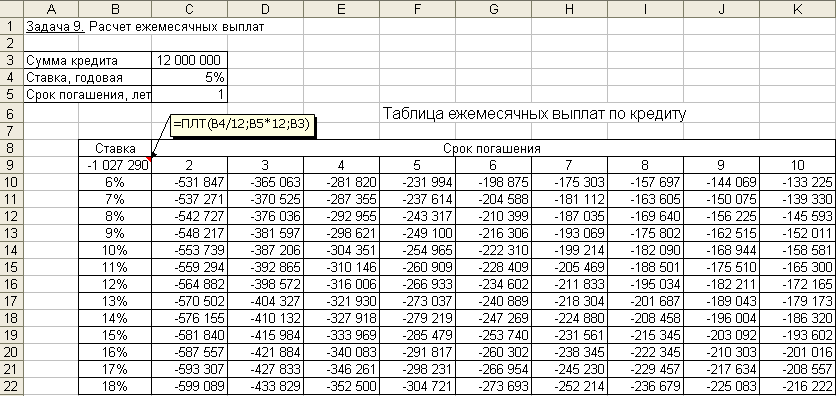 Рис. 4.23. Фрагмент окна с таблицей ежемесячных выплат по кредиту 6. Потребитель занимает сумму 250 000$, подлежащую выплате в течение 10 лет при 12% годовых на ежемесячной основе. Какова сумма процента и основного капитала на первом году займа? Определение скорости оборота инвестицийДля решения задач данной темы используются функции: ВСД (значения; предположение) ЧИСТВНДОХ (значения; даты; предположение) МВСД (значения; ставка_финанс; ставка_реинвест) Функция ВСД рассчитывает внутреннюю ставку доходности для не обязательно равных, но периодических потоков денежных средств – платежей (отрицательные величины) и доходов (положительные величины) – на основе формулы (8). Итерационным методом подбирается норма дисконтирования, при которой чистая текущая стоимость периодических выплат и поступлений ЧПС = 0. Иными словами, находится значение параметра Ставка из формулы: где: Значениеi – суммарный размер i-го денежного потока на конец периода (поступления – со знаком «плюс», выплаты – со знаком «минус»); Ставка – внутренняя скорость оборота для регулярных денежных потоков переменной величины; n – число периодов движения денежных потоков (суммарное количество выплат и поступлений); i – номер периода денежного потока. Функция ЧИСТВНДОХ возвращает внутреннюю ставку доходности для графика переменных, не обязательно периодических денежных потоков. Результат Ставка подбирается путем итераций из формулы (4.11), в которой чистая текущая стоимость нерегулярных переменных выплат и поступлений Чистнз = 0: 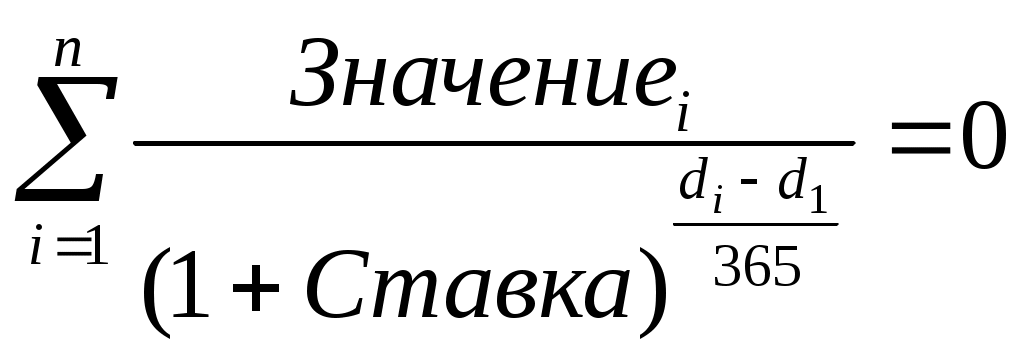 (4.16) (4.16)где: Ставка – внутренняя скорость оборота для нерегулярных денежных потоков переменной величины; d1 – дата 1-й операции (начальная дата); di – дата i-й операции; Значениеi – суммарное значение i–й операции; n – количество выплат и поступлений. Вычисления в функциях ВСД и ЧИСТВНДОХ выполняются в цикле, начиная со значения аргумента Предположение, и длятся до тех пор, пока результат не получится с точностью 0,00001% или пока количество итераций не превысит 20. В последнем случае считается, что решения нет, и для повторного поиска решения следует изменить значение аргумента Предположение, выбирая его из интервала между 0 и 1. Обычно аргумент Предположение в функциях не задается, по умолчанию он полагается равным 10%. Функция МВСД возвращает модифицированную внутреннюю ставку доходности для ряда периодических денежных потоков, учитывающую как затраты на привлечение инвестиции, так и процент, получаемый от реинвестирования денежных средств. Для определения порядка выплат и поступлений используется порядок расположения чисел в аргументе Значения: денежные потоки должны быть указаны в нужной последовательности и с правильными знаками (положительные значения для получаемых денег и отрицательные значения для выплачиваемых). Расчет значения МВСД выполняется по формуле: где: ЧПС – чистая приведенная стоимость (функция ЧПС); n–количество чисел в аргументе Значения функции МВСД; поступления – положительные денежные потоки (доходы); выплаты – отрицательные денежные потоки (расходы, вложения); r – аргумент ставка_реинвест, ставка реинвестирования на получаемые денежные потоки (поступления); f – аргумент ставка_финанс, ставка процента за деньги, используемые в денежных потоках (за выплаты). Если известна рыночная норма дохода k, то вычисленное с помощью указанных функций значение Ставка можно использовать в качестве оценки целесообразности принятия того или иного инвестиционного проекта. Проект принимается, если найденное значение Ставка > k и отвергается, если Ставка < k. Основанием для такого решения является то, что при Ставка < k ожидаемых доходов от проекта недостаточно для покрытия всех финансовых расходов, следовательно, принятие такого проекта является экономически невыгодным. При значении Ставка > k инвестор за счет доходов от проекта сможет не только выполнить все финансовые обязательства, но и получить прибыль. Очевидно, что такой проект экономически выгоден, и его следует принять. Задача 1. Постановка задачи. Определить внутреннюю норму дохода проекта, если затраты по проекту составят – 100 млн. руб., а ожидаемые в течение последующих четырех лет доходы будут: 40, 10, 20, 60 млн. руб. Дать оценку проекта, если рыночная норма дохода составляет 11%. Алгоритм решения задачи. Внутренняя норма дохода проекта рассчитывается с использованием функции ВСД. Подставив исходные данные в функцию, получим результат, представленный на рис. 4.24. Непосредственный ввод аргументов в функцию дает то же значение: =ВСД ({-100;40;10;20;60})= 10,27% Вывод. Проект следует считать невыгодным, поскольку в нашем случае внутренняя норма дохода – 10,27% меньше рыночной нормы дохода – 11%. Определим размер первоначальных затрат, чтобы проект стал выгодным. Для этого воспользуемся средством Подбор параметра из менюкоманды Сервис. Задав в появившемся диалоговом окне требуемое значение внутренней ставки доходности Всд (например, 11,1%), получим, что для экономической выгодности проекта первоначальные затраты должны составлять не более 98 071 355 руб. 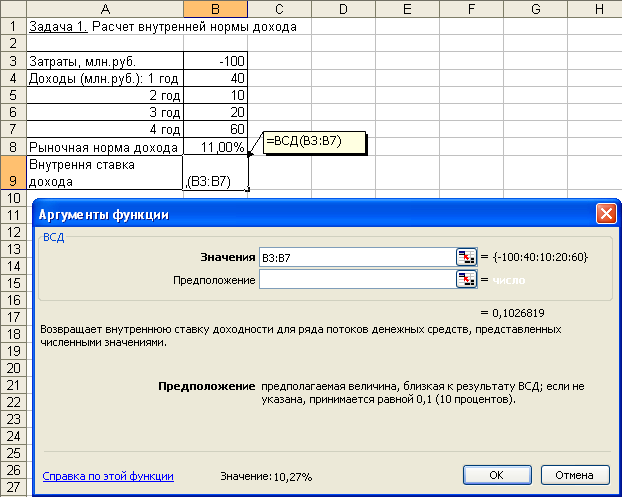 Рис. 4.24. Иллюстрация использования функции ВСД Задача 2. Постановка задачи. Определить внутреннюю норму дохода проекта, если затраты по проекту на 1.04.2005 г. составили 160 млн. руб., а ожидаемые доходы следующие: на 15.07.2005 г. – 50 млн. руб.; на 19.09.2005 г. – 80 млн. руб.; на 25.12.2005 г. – 90 млн. руб. Алгоритм решения задачи. В данной задаче имеют место нерегулярные поступления и выплаты переменной величины, для решения воспользуемся функцией ЧИСТВНДОХ. Построим таблицу и заполним ее исходными данными. В результате вычислений получим значение – внутренняя ставка доходности проекта – 83,10% (рис. 4.25). Проект выгоден. 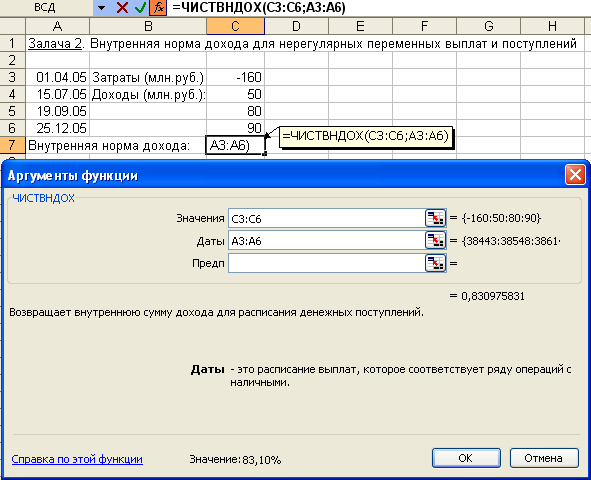 Рис. 4.25. Иллюстрация использования функции ЧИСТВНДОХ Задача 3. Постановка задачи. В организацию бизнеса фирма предполагает вложить 1 000 000 руб., взятых в кредит на 5 лет под 10% годовых. Предполагаемые доходы от хозяйственной деятельности планируется реинвестировать в другой проект под 12% годовых. 1) Рассчитать модифицированную ставку доходности по истечении каждого из 5 лет, если планируются следующие предполагаемые показатели доходов: за 1 год – 120 000 руб.; за 2 год – 300 000 руб., за 3 год – 400 000 руб., за 4 год – 380 000 руб., за 5 год – 420 000 руб. 2) Выполнить расчеты при тех же показателях, но с учетом 14% ставки реинвестирования. Алгоритм решения задачи. Для решения задачи представим исходные данные в ячейках листа и воспользуемся функцией МВСД. Результаты расчетов представлены на рис. 4.26. Для примера приведем формулу записи функции МВСД с непосредственным заданием значений аргументов при расчете модифицированной ставки доходности проекта за 5 лет при ставке реинвестирования 14%: =МВСД ({-1000000;120000;300000;400000;380000;420000};10%;14%) = 15,10% Аналогичный расчет выполним с применением формулы (4.17). Обратим внимание, что и в числителе, и в знаменателе следует указать результат функции ЧПС. Все результаты совпадают. 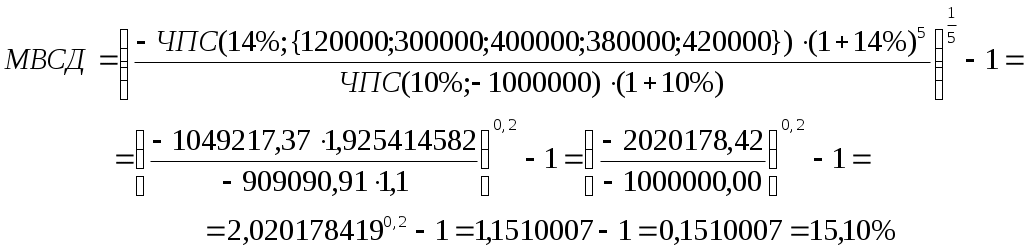 Задания для самостоятельной работы.
Определить внутреннюю норму доходности проекта. Оценить экономическую эффективность проекта с учетом рыночной нормы дохода – соответственно равной 11%; 12%; 15% (проверку выгодности проекта осуществлять функцией ЕСЛИ()). 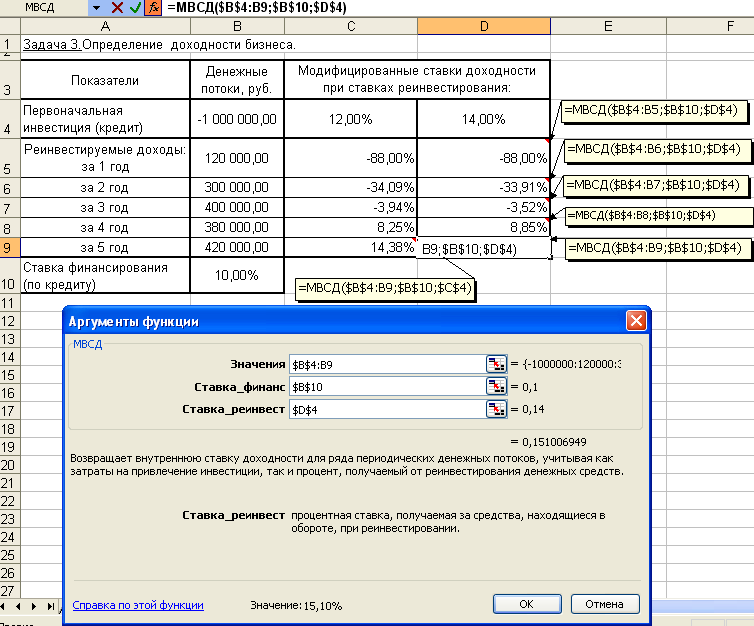 Рис. 4.26. Иллюстрация использования функции МВСД 2. Определить первоначальные затраты по проекту, если известно, что в последующие 4 года ожидаемые доходы будут соответственно: 300, 100, 400, 700 тыс. руб., при 9% норме дохода по проекту. 3. Определить внутреннюю скорость оборота инвестиции размером 55 тыс. руб., если в течение последующих 3 лет ожидаются годовые доходы соответственно: 9 тыс. руб., 17 тыс. руб., 23 тыс. руб.; на четвертый год ожидается убыток в размере 11 тыс. руб., а на пятый год – доход в размере 20 тыс. руб.
Рассчитать внутреннюю ставку доходности проекта. Рассчитать модифицированную ставку доходности проекта по истечении 4 лет, если все доходы реинвестировать в другой проект по ставке 15% годовых. Оценить экономическую эффективность проекта с учетом рыночной нормы дохода равной 11% (без реинвестирования доходов и с реинвестированием доходов). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
