Ответы на экзамен строительной механики. Строительная механика. 1. Теория упругости
 Скачать 135.69 Kb. Скачать 135.69 Kb.
|
|
Строительная механика, ответы 1. Теория упругости 1. Какие виды деформаций известны? Деформации бывают линейными и угловые. 3. Какие величины фигурируют в соотношениях Коши?  Деформации и перемещения 4. Какие величины фигурируют в уравнениях совместности деформаций? 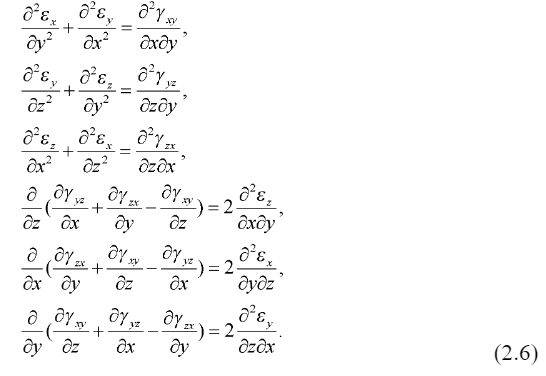 Линейные деформации, угловые деформации 5. Когда используются уравнения совместности деформаций? Когда задача статически неопределима. 6. Какие напряжения мы определяем для пространственного тела? Три нормальные и три касательных. 7. Какие зависимости связывают напряжения и объемные внешние силы? 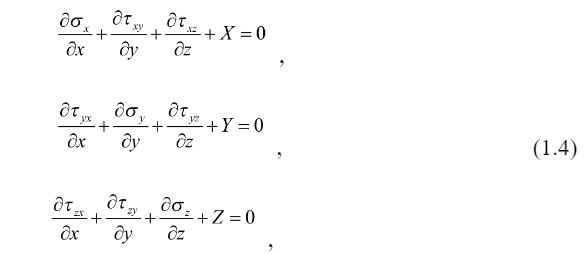 Уравнения равновесия в объеме 8. Какие зависимости связывают напряжения напряжения и поверхностные внешние силы? 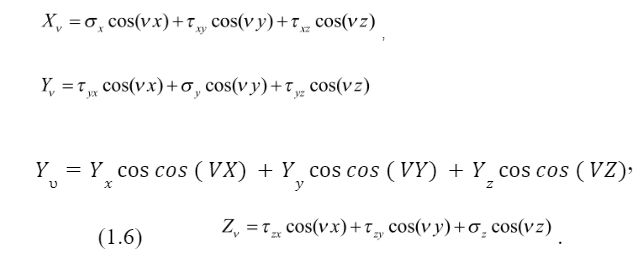 Уравнения равновесия на поверхности (условия на поверхности) 9. Что такое обобщенный закон Гука? Закон, согласно которому составляющие деформаций являются линейными функциями составляющих напряжений. 10. Какое упругое тело называется изотропным и сколько независимых упругих постоянных у изотропного тела? Упругое тело называется изотропным, если его упругие свойства одинаковы для всех направлений. Два (E и мю). 11. Какое состояние называется плоским напряженным и в каких телах реализуется плоское напряженное состояние? Плоским принимается напряженное состояние, когда рассматриваются напряжения, относящиеся только к плоскости хОу, а другие приравниваются к нулю. Плоское напряженное состояние с некоторым приближением реализуется в теле, размер которого в направлении оси Оz весьма мал, т.е. в тонкой плоской пластинке. 12. Какое состояние называется плоским деформированным и в каких телах реализуется плоское деформированное состояние? Деформированное состояние является плоским, т.е. рассматриваются деформации, относящиеся только к плоскости хОу, а остальные приравниваются нулю. Реализуется с некоторым приближением в длинном призматическом теле, нагруженном равномерно распределенной вдоль оси поверхностной нагрузкой. 13. Какое уравнение является разрешающим в плоской задаче и как можно найти решение этого уравнения?  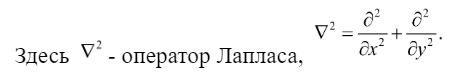 Обратный метод, интегрирование, метод разделения переменных. 14. Схема решения задачи теории упругости в перемещениях Исключить из системы уравнений равновесия напряжения с помощью физических отношений, а деформации с помощью соотношений Коши. Получаем три уравнения только с перемещениями. Интегрируем, и в обратном порядке определяем деформации и напряжения. И затем определяем произволы и константы с помощью граничных условий. 15. Схема решения задачи теории упругости в напряжениях. К системе уравнений равновесия добавить уравнения совместности деформаций, преобразованные с помощью физических соотношений в уравнения в напряжениях. Интегрируем, получаем решение для функций напряжений с точностью до констант и произволов. Далее деформации определяем с помощью физ. отношений, а перемещения с помощью интегрирования уравнений Коши. |
