Уравнение. Уравнение Бернулли. 1 Уравнение Бернулли

• Название: 1 Уравнение Бернулли
• Анкор: Уравнение
• Дата: 03.05.2023
• Размер: 84.3 Kb.
• Имя файла: Уравнение Бернулли.docx
• Тип: Закон; #1105649

1 Уравнение Бернулли

Уравнение Бернулли является одним из следствий закона сохранения энергии. Для вывода этого уравнения рассмотрим установившееся движение газа или жидкости в элементарной струйке, под которой мы будем понимать жидкость, текущую внутри некоторой замкнутой поверхности, образованной траекториями частиц жидкости. Жидкость будем считать идеальной, т.е. лишённой вязкости.

Также мы будем полагать, что в текущей жидкости (газе) отсутствуют потери теплового и механического характера.

Проведём условную поверхность уровня, представляющую собой горизонтальную плоскость, след которой на рисунке 1 изображён горизонтальной прямой ОО₁.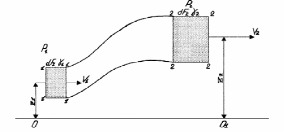



Рисунок 1- Поверхность уровня

Выделим в струйке два сечения 1 и 2 и посмотрим, какие виды энергии за 1 сек. поступают в струйку через сечение 1 и выходят через сечение 2.

Рассмотрим задачу несколько шире, чем это было сделано самим Д. Бернулли в 1738 г., и постараемся учесть все виды энергии, характерные для рассматриваемого процесса.

Энергия веса. Произвольный объём газа или жидкости протекающий через сечение 1, расположенное на высоте Z₁ от поверхности уровня, обладает определённой потенциальной энергией веса. Для того, чтобы подсчитать эту энергию, нужно помножить вес рассматриваемого объема на высоту Z₁, называемую нивелирной высотой. Так как мы рассматриваем секундный объём жидкости, равный dF₁V₁γ₁Z₁. Если же мы отнесем эту энергию к единице веса протекающей жидкости, т.е. 1 кг, то энергия веса одного кг протекающей жидкости составит: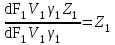

, [м] (2.1)
Энергия давления. Потенциальная энергия давления, которой обладает газ или жидкость в сечении, может быть определена из следующих соображений. Представим себе в сечении 1 поршень, движущийся в направлении движения жидкости со скоростью V₁. Тогда энергия давления частиц жидкости будет равна работе, произведённой поршнем в единицу времени, т.е. произведе­ние давления Р₁ на площадь сечения струйки dF₁ и на скорость течения жидко­сти V₁, т.е. 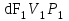. Отнеся эту энергию к 1 кг жидкости, получим для энергии давления следующее выражение:

, [м] (2.2)

Кинетическая энергия. Кинетическая энергия частиц газа или жидкости, протекающих через сечение 1 равны:

, (2.3)

так как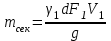



Относя эту величину к 1 кг жидкости, получим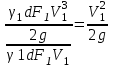

[м] (2.4)

Внутренняя тепловая энергия. Ввиду того, что мы составляем уравнение энергии для произвольной жидкости и газа, необходимо рассмотреть также и внутреннюю тепловую энергию. Внутренняя энергия выражается обыч­но в больших калориях на один килограмм веса газа и обозначается через И₁.

Для выражения этого вида энергии в тех же единицах измерения, что и другие виды энергии, выразим внутреннюю тепловую энергию в механических единицах, воспользовавшись тепловым эквивалентом работы А. Тогда внутренняя энергия 1 кг жидкости протекающей через сечение 1, будет равна: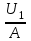

[м]

Поскольку другие виды энергии: электромагнитная, химическая, и т.п. не характерны для рассматриваемого процесса течения, будем считать, что перечисленные виды исчерпывают задачу отыскания полной энергии, вносимой жидкостью через сечение 1 в единицу времени. Полная энергия в сечении 1, отнесенная к 1 кг жидкости, определяется суммой четырёх перечисленных выше видов энергии:

, (2.5)

Рассматривая протекание жидкости через сечение 2, мы можем составить выражение для полной энергии струйки в этом сечении, которая будет совершенно аналогично выражению, написанному для сечения 1

, (2.6)

Ввиду того, что движение жидкости в струйке установившееся, трение от­сутствует, передача энергии через стенки струйки так же отсутствует, полная энергия жидкости, втекающей через сечение 1, должна равняться полной энер­гии жидкости, вытекающей через сечение 2. Приравнивая соответствующие вы­ражения, получим обобщенное уравнение Бернулли для газа:

(2.7)

Для несжимаемой жидкости: γ1=γ2=γ; U₁=U₂; ρ=const и уравнение 2.7 примет вид, в котором его получил Д. Бернулли: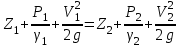

,

Пред выводом уравнения мы полагаем, что в текущем газе отсутствуют потери теплового и механического характера. Если же между двумя рассматриваемыми сечениями струйки существует, например, потери тепла и трения (которое, в конечном счете, также переходит в тепло), или происходит подвод энер­гии, то в зависимости от величины скорости течения картина может быть раз­личной.

Отбрасывая мало интересный случай очень медленных течений, рассмот­рим течение газа (жидкости) при больших скоростях. В данном случае тепло (например, тепло трения) не успевает утечь из потока и течение можно считать без теплообмена адиабатическим. При средних скоростях течения теплообмен существует, и для того, чтобы величина Е₁ и Е₂ были равны друг друга, необхо­димо ввести в уравнение Бернулли поправку.

Если допустим в струйке существование потерь энергии между сечениями 1 и 2 (механического или теплового характера которые называют гидравличе­скими потерями), то полная энергия в сечении 1 будет отличаться от полной энергии в сечении 2 на величину потерь h_r. т.е.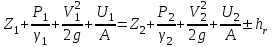

, (2.8)

Гидравлические потери зависят от формы, размеров шероховатости русла, от скорости течения и вязкости жидкости, но практически не зависит от абсо­лютного значения давления в жидкости. Для несжимаемой жидкости соответственно: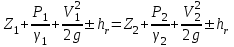

, (2.9)

Во все приведённых выше выражениях каждый из видов энергий отнесён к 1 кг жидкости и выражен в метрах. Поэтому Z часто называют нивелирной вы­сотой, соответственно:

- пьезометрическая высота;

- скоростная высота;

- тепловая высота;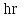

- высота потерь.

В аэродинамике часто уравнение 2.9 пишут в ином виде, отнеся энергию не к одному килограмму, а к одному кубическому метру текущей жидкости. В уравнении 2.9 этого можно достичь путём умножения величины Е₁ и Е₂ на γ. Получается так называемое уравнение напоров: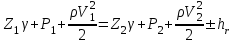

, (2.10)

В этом уравнении размерность энергии (кг*м^-2). Сумма всех членов левой части уравнения Бернулли для несжимаемой среды называют полным напором.

zγ - аэростатическое давление (гидростатическое),

р - статическое давление;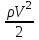

- динамическое давление;

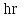- потерянный напор.

Скоростной напор обозначается: ,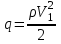

Применение уравнения Бернулли в технике столь широко, что даже про­стое перечисление займет много времени и места, поэтому мы остановимся на нескольких конкретных случаях, а два из них постараемся подробно проанализи­ровать.