|
|
геометрия. Зачет_по_геометрии_Параллельные_прямые_7_класс. 1 вариант фио класс
1 ВАРИАНТ
|
ФИО
|
класс
|
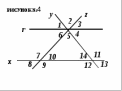
Задание 1 На рисунке изображены прямые а , в и секущая с . Какое условие должно выполняться, чтобы прямые а и в были параллельны (рис №1).

|

|
Задание 2 Выберите верные утверждения.
1) Через любую точку на плоскости проходят две прямые параллельные данной прямой.
2) Две непересекающиеся прямые параллельны.
3) Если при пересечении двух прямых секущей односторонние углы равны, то прямые параллельны.
4) Две прямые перпендикулярные третьей параллельны.
5) Если при пересечении двух прямых смежные углы составляют 180°, то прямые параллельны.
|
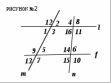
Задание 3 Прямые l и f параллельны, m и n – секущие (рис №2).
Выберите неверные утверждения.

|
|
Задание 4 Выберите неверное утверждение.
1) Если две прямые на плоскости не имеют общих точек, то они параллельны.
2) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
3) Через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.
4) Если две прямые параллельны третьей прямой, то они параллельны между собой.
5) Если две параллельные прямые пересечены секущей, то односторонние углы равны.
|
Задание 5 Данное утверждение «Если две параллельные прямые пересечены секущей, то соответственные углы равны» является:
1) Третьим свойством параллельных прямых.
2) Первым признаком параллельных прямых.
3) Первым свойством параллельных прямых.
4) Вторым признаком параллельных прямых.
5) Вторым свойством параллельных прямых.
|
Задание 6 Прямые а║в, c║d (рис №3). Какое равенство является неверным.

|

|
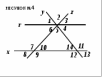
Задание 7 Если прямые r и x параллельны (рис №4), то неверно …

|
|
Задание 8 Аксиома параллельных прямых – это аксиома …
1)Архимеда. 2) Евклида. 3) Лобачевского. 4) Атанасяна. 5) Пифагора.
|
Задание 9 Теорема «Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны» является для теоремы «Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны» ….
1) Свойством.
2) Следствием.
3) Условием.
4) Обратной теоремой.
5) Признаком
|
Задание 10 В теореме «Если две прямые параллельны третьей прямой, то они параллельны между собой», различают две части, которые называются:
1) Условие и заключение.
2) Начало и конец.
3) Первая часть и вторая часть.
4) Достаточное и необходимое условия.
5) Прямая и обратная части.
|
Задание 11 Рисунок соответствует (рисунок №5.1)….
1) Признаку параллельности прямых через соответственные углы.
2) Свойству параллельных прямых через накрест лежащие углы.
3) Следствию, о том, что прямая, пересекающая одну
из параллельных прямых, пересекает и другую.
4) Аксиоме, что через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.
5) Свойству параллельных прямых через соответственные углы.
|

|
Задание 12 Пятый постулат Евклида формулируется так…
1) Две различные прямые имеют не более одной общей точки.
2) Через точку, не лежащую на данной прямой, проходят две прямые параллельные данной.
3) Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и к другой.
4) Через точку, не лежащую на данной прямой, проходит только одна прямая параллельная данной.
5) Две прямые перпендикулярные к третьей, параллельны.
|
Задание 13 При доказательстве следствий из аксиомы о параллельных прямых используют метод …
1) от простого к сложному
2) от противного
3) по действиям
4) проб и ошибок
5) рассуждений.
|
Задание 14 Для построения параллельных прямых на практике не используют:
1) теодолит
2) рейсшина
3) линейка и угольник
4) малка
5) линейка и циркуль.
|
Задание 15 Какой теореме соответствует данное доказательство (рис №6).
«Углы 2 и 3 вертикальные, тогда они равны по свойству вертикальных углов. Значит 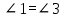 по условию, по условию,  по решению, то по решению, то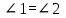 . Но углы 1 и 2 накрест лежащие при пресечении прямых m и n секущей с, тогда по первому признаку параллельных прямых m║n. ч.т.д.» . Но углы 1 и 2 накрест лежащие при пресечении прямых m и n секущей с, тогда по первому признаку параллельных прямых m║n. ч.т.д.»
1) Свойство накрест лежащих углов, образованных при пересечении параллельных прямых секущей.
2) Признак параллельности прямых через накрест лежащие углы.
3) Признак параллельности прямых через соответственные углы.
4) Свойство соответственных углов, образованных при пересечении параллельных прямых секущей.
5) Признак параллельности прямых через односторонние углы.
|

|
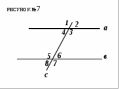
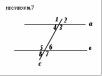
Задание 16 При пересечении двух параллельных прямых секущей один из образованных углов на рисунке равен 49°. Найдите углы (рис №7) 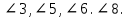
Ответ:
1) 131°, 131°,49°,49°.
2) 141°,131°,39°,49°.
3) 49°,49°,121°,121°.
4) 131°,49°,141°,121°.
5) 49°,49°,131°,131°.
|
|
Задание 17 Продолжите предложение, чтобы оно стало верным утверждением : «Если прямая перпендикулярна к одной из двух параллельных прямых, то …»
1) они все пересекутся в одной точке;
2) они все параллельны;
3) она параллельна к другой;
4) она перпендикулярна и к другой;
5) она пересекает другую.
|
Задание 18 Если прямые r и x параллельны, 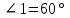 . Найдите градусные меры углов (рис №4) . Найдите градусные меры углов (рис №4) 
1) 60°, 60°,120°.
2) 60°, 70°,110°.
3) 120°, 60°,120°.
4) 40°, 60°,120°.
5) 60°, 60°,60°.
|
|
Задание 19 Укажите теорему, которая имеет условие «при пересечении двух прямых секущей односторонние углы в сумме составляют 180°», заключение – «прямые параллельны».
1) Если при пересечении двух прямых секущей односторонние углы в сумме составляют 180°, то прямые не параллельны.
2) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
3) Если при пересечении двух прямых секущей односторонние углы в сумме составляют 180°, то прямые параллельны.
4) Если две прямые пересечены секущей, то сумма односторонних углов равна 180°.
5) Если две параллельные прямые пересечены секущей, то сумма односторонних углов не равна 180°.
|
Задание 20 Укажите обратную теорему к данной теореме: «Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны».
1) Если параллельные прямые пересечены секущей, то соответственные углы равны.
2) Если при пересечении двух прямых секущей соответственные углы не равны, то прямые не параллельны.
3) Если не параллельные прямые пересечены секущей, то соответственные углы не равны.
4) Для данной теоремы нет обратной.
5) Если две прямые пересечены секущей, то соответственные углы равны.
|
Задание 21 На каком из пяти рисунков (рисунок №8.1) прямые m и n параллельны по признаку: «Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны».
1)
2)
3)
4)
5)
|
|
Задание 22 К какой теореме относится это доказательство, дополните его, чтобы рассуждения были верными (рисунок №10.1).

Известно, что прямые а║в пересечены секущей с. Докажем, что углы 1 и 2 равны.
На рисунке углы 1 и 3 –______________, значит они равны. Углы 2 и 3 накрест лежащие углы при пересечении прямых а║в секущей с, тогда они равны по ____________. Если 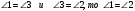 . Ч.т.д. . Ч.т.д.
1) Первое свойство параллельных прямых; соответственные углы; по 2 свойству параллельных прямых
2) Второй признак параллельных прямых; вертикальные углы; по 1 свойству параллельных прямых.
3). Второе свойство параллельных прямых; вертикальные углы; по 1 свойству параллельных прямых.
4) Первый признак параллельных прямых; соответственные углы; по 1 признаку параллельных прямых.
5) Второе свойство параллельных прямых; вертикальные углы; по 1 признаку параллельных прямых.
|
Задание 23 Заполните пропуски в формулировке теоремы
Если стороны одного угла __________________________параллельны __________________________другого угла, то
______________________________________________________________________________________________________
______________________________________________________________________________________________________
|
Задание 24 Найдите градусные меры углов 1 и 2 (рис №9), если 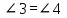 , а , а 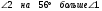
Решение
Ответ
|

|
Впишите ответы в таблицу, по номерам кроме 23 задания.
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
|
|
|
|
|
|
|
|
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
|
|
|
|
|
|
|
|
|
21
|
22
|
23
|
24
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Количество верных ответов ______________________
Оценка__________________________
2 ВАРИАНТ
|
ФИО
|
класс
|
Задание 1 На рисунке изображены прямые а , в и секущая с . Какое условие должно выполняться, чтобы прямые а и в были параллельны (рис №1).
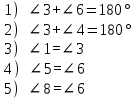
|

|
Задание 2 Выберите верные утверждения.
1) Если при пересечении двух прямых секущей вертикальные углы равны, то прямые параллельны. Если
2) Две прямые параллельные третьей перпендикулярны..
3) Если две прямые не пересекаются, то они параллельны.
4) прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
5) Любые две прямые на плоскости параллельны.
|
Задание 3 Прямые l и f параллельны, m и n – секущие (рис№2). Выберите верные утверждения.
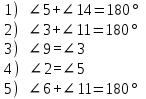
|
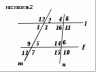
|
Задание 4 Выберите неверное утверждение.
1) Если две прямые на плоскости не имеют общих точек, то они параллельны.
2) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
3)Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны..
4) Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
5) Через точку, не лежащую на данной прямой проходят прямые, параллельные данной.
|
Задание 5 Данное утверждение «Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны» является:
1) Первым признаком параллельных прямых
2) Первым свойством параллельных прямых
3) Вторым свойством параллельных прямых.
4) Вторым признаком параллельных прямых.
5) Третьим свойством параллельных прямых.
|
Задание 6 Прямые а║в, c║d (рис №3). Какое равенство является неверным.

|

|
Задание 7 Если прямые r и x параллельны (рис №4), то неверно …

|
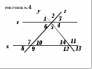
|
Задание 8 Аксиома параллельных прямых – это аксиома …
1) Инков 2) Пифагора 3) Ломоносова 4) Народная. 5) Евклида. .
|
Задание 9 Теорема «Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°» является для теоремы «Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны» ….
1) Следствием.
2) Прямой теоремой.
3) Обратной теоремой.
4) Заключением.
5) Признаком.
|
Задание 10 В теореме «Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны» различают две части, которые называются:
1) Условие и заключение.
2) Начало и конец.
3) Первая часть и вторая часть.
4) Достаточное и необходимое условия.
5) Прямая и обратная части.
|
Задание 11 Рисунок соответствует доказательству (рисунок №5.2)….
1) Аксиоме, что через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.
2) Свойства параллельных прямых через накрест лежащие углы.
3) Признака параллельности прямых через соответственные углы.
4) Следствия, о том, что если две прямые параллельны третьей прямой, то они параллельны.
5) Свойства параллельных прямых через соответственные углы.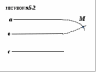
|
Задание 12 Определение параллельных прямых формулируется так…
1) Две прямые на плоскости называются параллельными, если они не пересекаются.
2) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
3) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
4) Две прямые перпендикулярные к третьей, параллельны
5) Если две прямые перпендикулярны третьей прямой, то они параллельны.
|
Задание 13 При доказательстве свойства параллельных прямых через накрест лежащие углы использую метод …
1) рассуждений.
2) по действиям
3) проб и ошибок
4) от простого к сложному
5) от противного
|
Задание 14 Для построения параллельных прямых на практике не используются:
1) штангенциркуль
2) рейсшина
3) линейка и угольник
4) малка
5) линейка и циркуль.
|
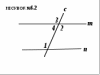
Задание 15 Какой теореме соответствует данное доказательство (рисунок №6.2).
«Углы 2 и 4 смежные , тогда их сумма равна 180° по свойству смежных углов. Значит  по условию, по условию,  по решению, то по решению, то . Но углы 1 и 2 накрест лежащие при пресечении прямых m и n секущей с, тогда по первому признаку параллельных прямых m║n. ч.т.д.» . Но углы 1 и 2 накрест лежащие при пресечении прямых m и n секущей с, тогда по первому признаку параллельных прямых m║n. ч.т.д.»
1) Признак параллельности прямых через соответственные углы.
2) Признак параллельности прямых через накрест лежащие углы.
3) Свойство односторонних углов, образованных при пересечении параллельных прямых секущей.
4) Свойство соответственных углов, образованных при пересечении параллельных прямых секущей.
5) Признак параллельности прямых через односторонние углы.
|
|
Задание 16 При пересечении двух параллельных прямых секущей один из образованных углов на рисунке равен 106°. Найдите углы 
1) 106°, 106°,74°,74°.
2) 116°,106°,64°,74°.
3) 127°,127°,53°,53°.
4) 106°,106°,64°,164°.
5) 64°,64°,106°,106°.
|
|
Задание 17 Продолжите предложение, чтобы оно стало верным утверждением : «Если две прямые параллельны третьей прямой, то …»
1) они все параллельны;
2) они перпендикулярны;
3) они все пересекутся в одной точке;
4) они образуют прямоугольник;
5) соответственные углы равны
|
Задание 18 Если прямые r и x параллельны, 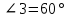 . Найдите градусные меры углов (рис №4) . Найдите градусные меры углов (рис №4) 
1) 60°, 60°,60°.
2) 60°, 70°,110°.
3) 40°, 60°,120°.
4) 60°, 60°,120°.
5) 120°, 60°,120°.
|

|
Задание 19 Укажите теорему, которая имеет условие
«при пересечении двух прямых секущей соответственные углы равны », заключение – «прямые параллельны».
1) Если при пересечении двух прямых секущей соответственные углы равны, то прямые не параллельны
2) Если две параллельные прямые пересечены секущей, то соответственные углы равны.
3). Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
4) Если две прямые пересечены секущей, то соответственные углы равны.
5) Если две параллельные прямые пересечены секущей, то соответственные углы не равны.
|
Задание 20 Укажите теорему, которая является обратной для теоремы с условием «две параллельные прямые пересечены секущей» и заключением «накрест лежащие углы равны».
1) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
2) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
3) Если две прямые пересечены секущей, то накрест лежащие углы не равны.
4) Если накрест лежащие углы при пересечении двух прямых секущей не равны, то прямые не параллельны.
5) Недостаточно данных.
|
Задание 21 На каком из пяти рисунков (рисунок №8.2) прямые m и n параллельны по признаку: «Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны».
1)
2)
3)
4)
5)

|
Задание 22 К какой теореме относится это доказательство, дополните его, чтобы рассуждения были верными (рисунок №10.2).
Известно, что прямые а║в пересечены секущей с. Докажем, что сумма углов 1 и 2 равна 180°.
На рисунке углы 1 и 3 –______________, значит они в сумме равны 180°. Углы 2 и 3 накрест лежащие углы при пересечении прямых а║в секущей с, тогда они равны по ____________. Если  . Ч.т.д. . Ч.т.д.
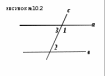
1) Третье свойство параллельных прямых; смежные углы; по 1 признаку параллельных прямых
2) Третий признак параллельных прямых; смежные углы; по 1 свойству параллельных прямых.
3). Третье свойство параллельных прямых; смежные углы; по 1 свойству параллельных прямых.
4) Первый признак параллельных прямых; односторонние углы; по 1 признаку параллельных прямых.
5) Второе свойство параллельных прямых; вертикальные углы; по 1 признаку параллельных прямых.
|
Задание 23 Заполните пропуски в формулировке следствия
Если прямая перпендикулярна к одной из двух ___________________________________прямых, то она __________
__________________________________________________________________________________________________
|
Задание 24 Найдите градусные меры углов 1 и 2 (рисунок №9), если 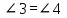 , а , а 
Решение
Ответ
|

|
Впишите ответы в таблицу, по номерам кроме 23 задания.
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
|
|
|
|
|
|
|
|
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
|
|
|
|
|
|
|
|
|
21
|
22
|
23
|
24
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
 Скачать 2.31 Mb.
Скачать 2.31 Mb.









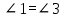 по условию,
по условию,  по решению, то
по решению, то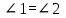 . Но углы 1 и 2 накрест лежащие при пресечении прямых m и n секущей с, тогда по первому признаку параллельных прямых m║n. ч.т.д.»
. Но углы 1 и 2 накрест лежащие при пресечении прямых m и n секущей с, тогда по первому признаку параллельных прямых m║n. ч.т.д.» 
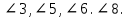

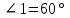 . Найдите градусные меры углов (рис №4)
. Найдите градусные меры углов (рис №4) 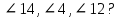



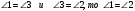 . Ч.т.д.
. Ч.т.д.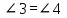 , а
, а 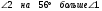

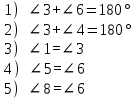

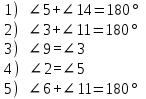





 по условию,
по условию,  по решению, то
по решению, то


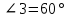 . Найдите градусные меры углов (рис №4)
. Найдите градусные меры углов (рис №4) 


 . Ч.т.д.
. Ч.т.д.

