1. Вывод формул для моментов инерции простейших фигур (прямоугольник, треугольник, круг) Прямоугольное сечение
 Скачать 0.73 Mb.
|
|
1. Вывод формул для моментов инерции простейших фигур (прямоугольник, треугольник, круг) Прямоугольное сечение. 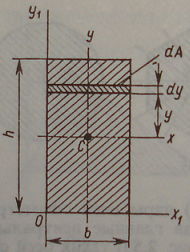 Прямоугольное сечение имеет две оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон. Главный центральный момент инерции относительно оси x  Элементарную площадку dA в этом случае можно представить в виде полоски во всю ширину сечения и толщиной dy, значит dA=b*dy. Подставим под знак интеграла значение dA и проинтегрировав по всей площади, т.е. в пределах изменения ординаты y от –h/2 до +h/2, получим  Окончательно  Аналогично получим формулу главного центрального момента инерции прямоугольника относительно оси y:  Круглое сечение 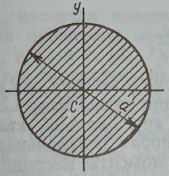 Для круга главные центральные моменты инерции относительно осей x и y равны между собой. Поэтому из равенства      Треугольник 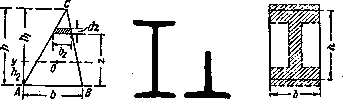 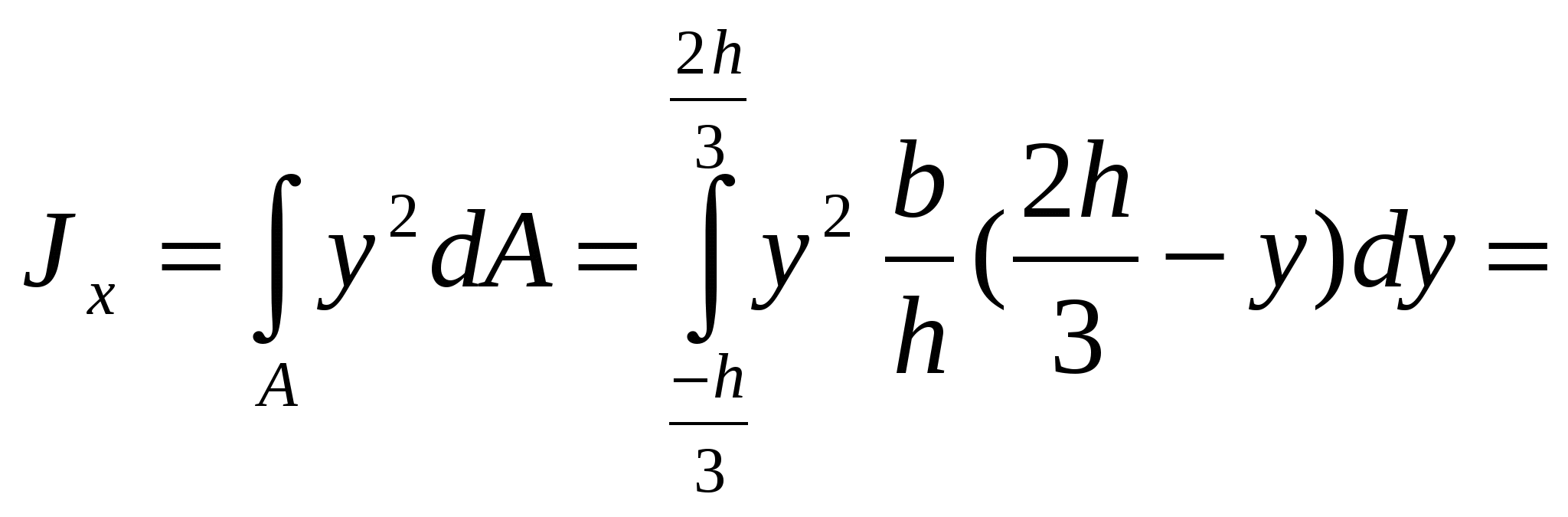 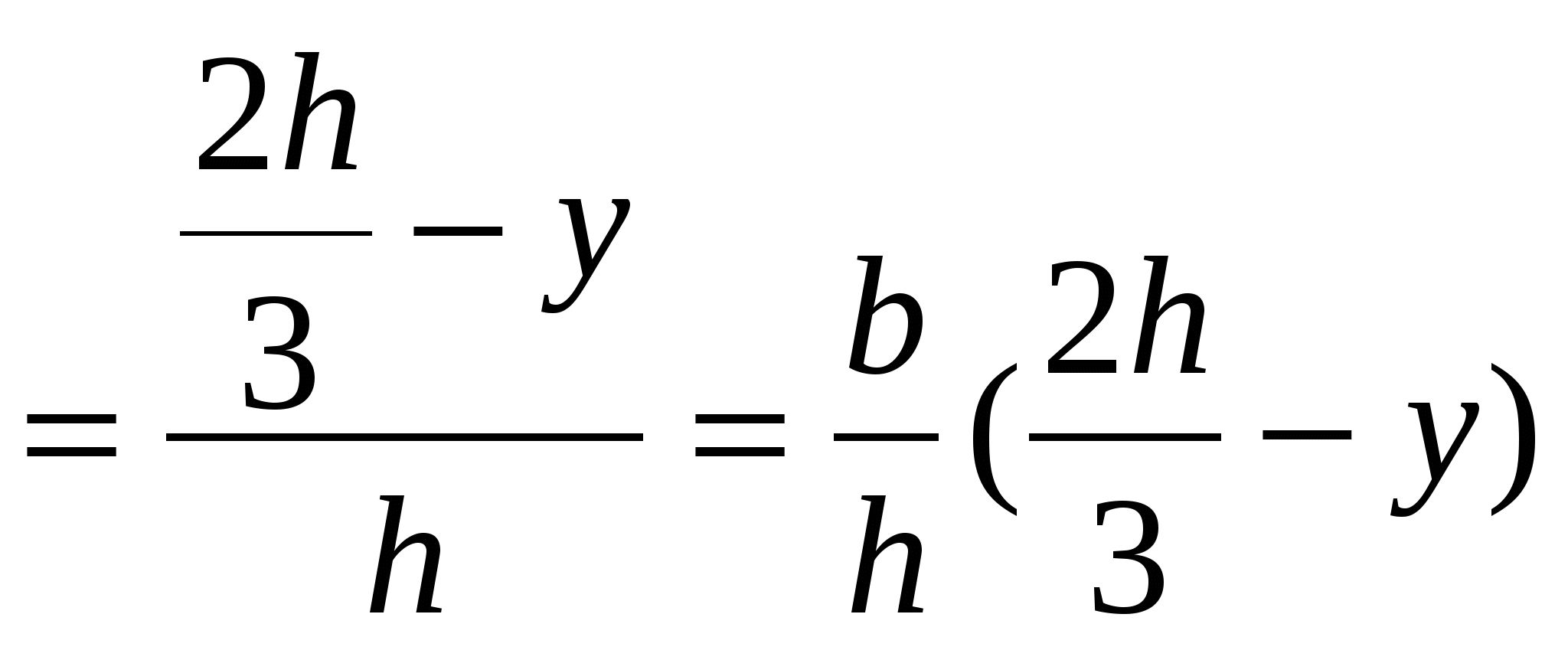   2.Изменение моментов инерции при переходе от центральных осей к параллельным:  Jx1=Jx + a2А; Jy1=Jy + b2А; момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. Jy1x1=Jyx + abF; ("a" и "b" подставляют в формулу с учетом их знака). 3.Изменение моментов инерции при повороте осей 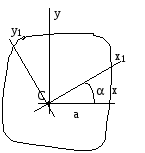 Jx1=Jxcos2 + Jysin2 — Jxysin2; Jy1=Jycos2 + Jxsin2 + Jxysin2; Jx1y1=  (Jx — Jy)sin2 + Jxycos2 ;Угол >0, если переход от старой системы координат к новой происходит против час.стр. Jy1 + Jx1= Jy + Jx Экстремальные (максимальное и минимальное) значения моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т.е. главные оси инерции — оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол, определяющий положение главных осей:  , если 0>0 оси поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей: 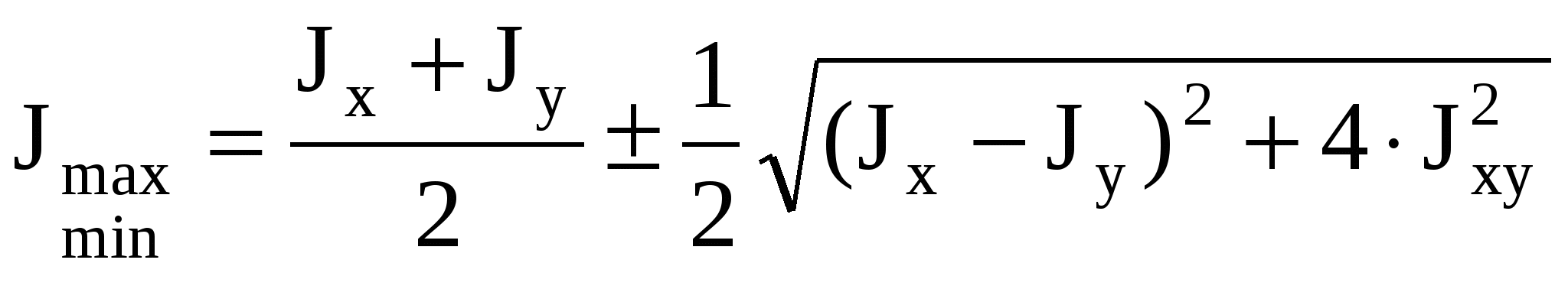 Jmax + Jmin= Jx + Jy. Центробежный момент инерции относительно главных центральных осей инерции равен 0. Если известны главные моменты инерции, то формулы перехода к повернутым осям: Jx1=Jmaxcos2 + Jminsin2; Jy1=Jmaxcos2 + Jminsin2; Jx1y1= (Jmax — Jmin)sin2;4.Классификация элементов конструкций Стержнем наз. Геом тела у которых один из размеров много больше других. Пластины или оболочки – это геом тела у которых один из размеров << других Массивные тела- все размеры одного порядка 5.Основные допущения о свойствах материала Однородные – в люб. точке материалы имеют одинак. физико-химич. св-ва; Сплошная среда – кристаллич. строение и микроскопич. дефекты не учитываются; Изотропны – механич. св-ва не зависят от направления нагружения; Идеальная упругость – полностью восстанавливают форму и размеры после снятия нагрузки. 6.Типы опор а) Шарнирно – неподвижная (двухсвязная) опора: Воспринимает как вертикальные, так и горизонтальные усилия (усилия под углом).  б) Шарнирно – подвижная опора – воспринимает только вертикальные нагрузки. Реакция опоры всегда направлена вдоль опорного стержня, перпендикулярно опорной поверхности в) Жесткая заделка (трехсвязная) 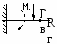 Реакции в опорах определяют из условия равновесия (уравнение статики). 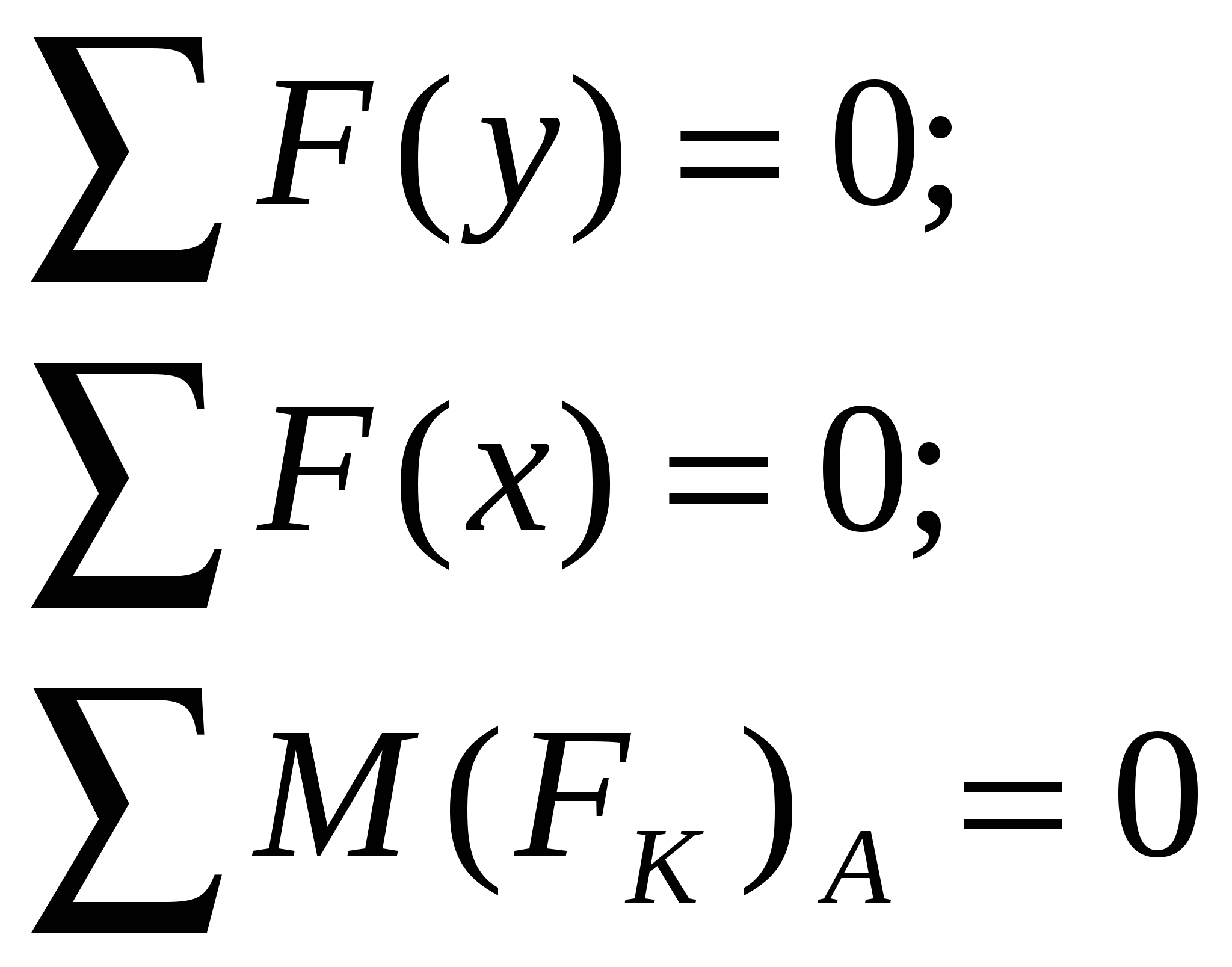 7.Классификация нагрузок
Поверхностные и объемные а) сосредоточенная сила б) распределенная сила  прямоугольная Rq= qa треугольная Rq= ½ qa в) сосредоточенный момент изгибающий скручивающий г) распределенный момент Rmz= mz a –равнодейств распр мом
Постоянные и временные
Статические и динамические
Активная(известны) и реактивная (неизвестны) 8.Основные принципы изучаемого курса При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения. принцип Сен-Венана на достаточном удалении от места приложения нагрузки характер её воздействия не зависит от способа её приложения, а зависит от величины равнодействующей. 9.Внутренние усилия. Метод сечений (Метод РОЗУ) 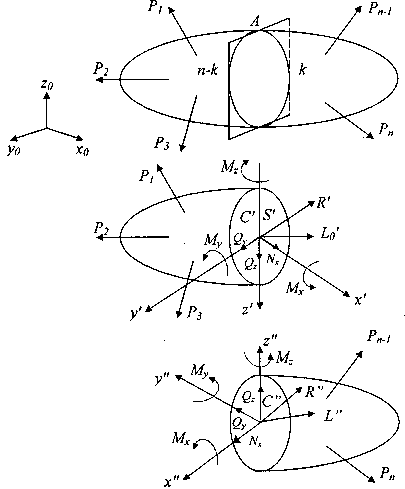 Nz=∑z (pi) нормальная с Qx=∑x (pi) поперечная с Qy=∑y (pi) Mz=∑mz (pi) крутящий момент Mx=∑mx (pi) изгибающий My=∑my (pi) Разрезаем мысл тело плоск Отбрасываем одну из г внутр усил Заменяем внутр усилиями Уравновешив внутр ус внеш нагр 10.Правило знаков внутренних усилий Правило знаков поперечных сил при изгибе:  Крутящий момент Против ЧС при взгляде со стороны сеч то + Правило знаков изгибающих моментов:  Правило проверки правильности построения эпюр нагружения: В сечениях балки, где приложены внешние сосредоточенные нагрузки на эпюре д.б. скачёк на величину этой нагрузки. 11.Эпюры внутренних усилий ПРИ РАСТЯЖЕНИИ-СЖАТИИ  ПРИ КРУЧЕНИИ  при прямом изгибе 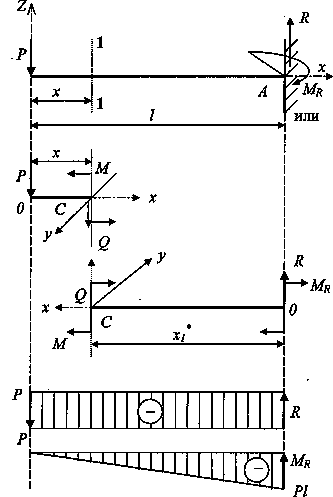 12.Дифференциальные зависимости при изгибе  ;  ;  13.Следствия из дифференциальных зависимостей
4. На участке где Qy>0 эпюра мх возрастает слева направо 5. В том сеч. где приложена сосред сила эпюра Qy имеет скачок на вел этой силы. В сеч где сосред момент эпюра мх имеет скачок на величену этого момента 14.Понятие о напряжениях. Нормальные и касательные напряжения Напряжение – численная мера распределения внутренних сил по плоскости поперечного сечения. Его используют при исследовании и определении внутренних сил любой конструкции. Выделим на плоскости сечения площадку A; по этой площадке будет действовать внутренняя сила R. Величина отношения R/A=pсрназывается средним напряжением на площадке A. Истинное напряжение в точке А получим устремив A к нулю:  Нормальные напряжения возникают, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц по плоскости рассматриваемого сечения. Очевидно, что  . Касательное напряжение в свою очередь может быть разложено по направлениям осей x и y (τzх, τzу). Размерность напряжений – Н/м2 (Па).При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела. 16.Закон парности касательных напряжений Касат. напряжение на 2-ух взаимно перпендик. площ. направлены к ребру или от ребра и равны по величине 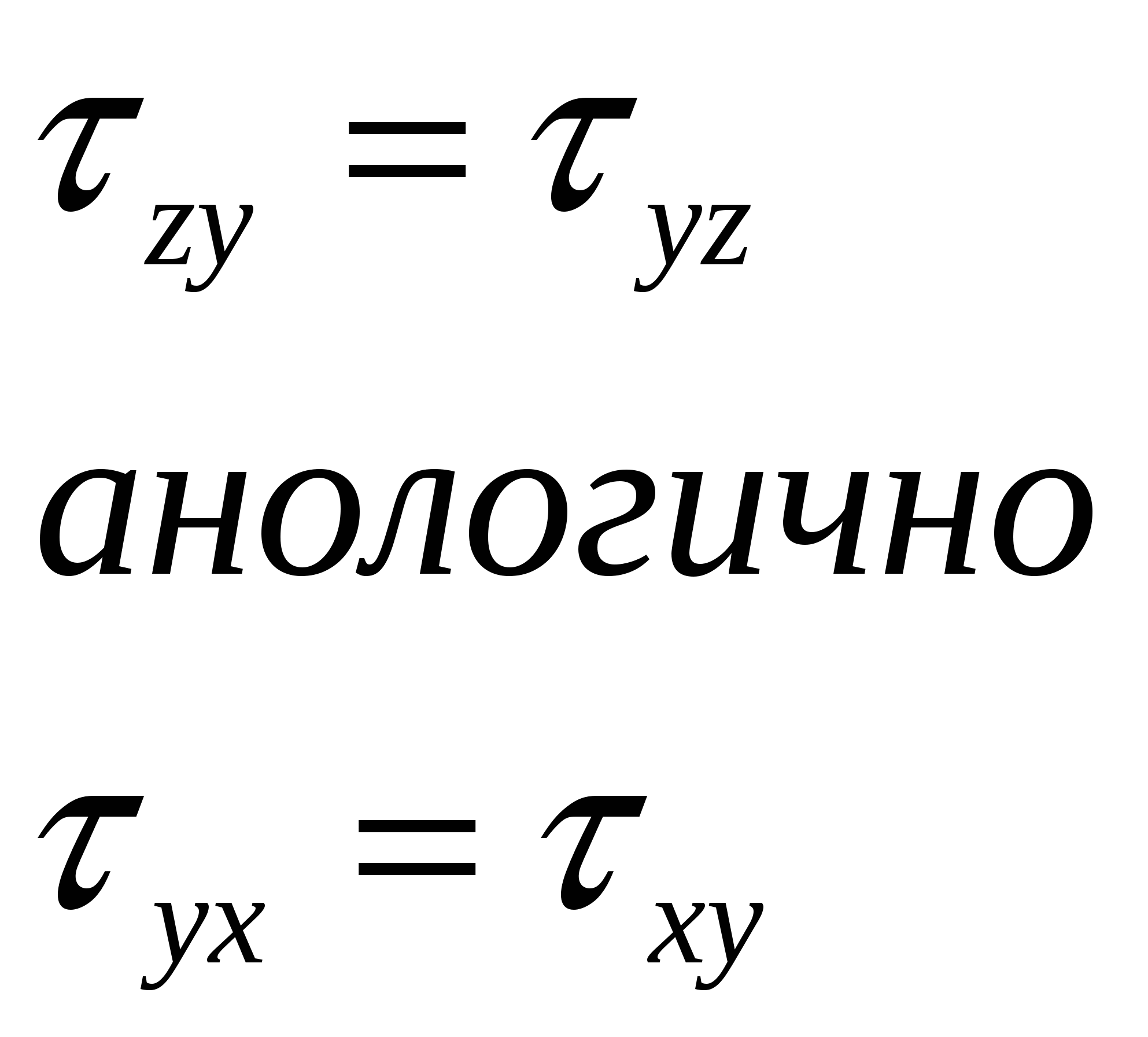 17.Понятие о деформациях. Мера линейной, поперечной и угловой деформации Деформац – наз. взаимное перемещение точек или сечений тела по сравн с полож-ями тела которые они занимали до приложения внеш сил бывают: упругие и пластические а) линейная деформация мерой явл относительное удлинение эпсила =l1-l/l б) поперечная деф мерой явл. относительное сужение эпсила штрих=|b1-b|/b 18.Гипотеза плоских сечений Основные гипотезы (допущения): гипотеза о не надавливании продольных волокон: волокна, параллельные оси балки, испытывают деформацию растяжения – сжатия и не оказывают давления друг на друга в поперечном направлении; гипотеза плоских сечений: сечение балки, плоское до деформации, остается плоским и нормальным к искривленной оси балки после деформации. При плоском изгибе в общем случае возникают внутренние силовые факторы: продольная сила N, поперечная сила Q и изгибающий момент М. N>0, если продольная сила растягивающая; при М>0 волокна сверху балки сжимаются, снизу растягиваются.  .Слой, в котором отсутствуют удлинения, называется нейтральным слоем (осью, линией). При N=0 и Q=0, имеем случай чистого изгиба. Нормальные напряжения:  , — радиус кривизны нейтрального слоя, y — расстояние от некоторого волокна до нейтрального слоя.19.Закон Гука (1670). Физический смысл входящих в него величин Он установил связь между напряжением, растяжением и продольной деформацией.  где Е – коэффициент пропорциональности (модуль упругости материала).Модуль упругости характеризует жёсткость материала, т.е. способность сопротивляться деформациям. (чем больше Е, тем менее растяжимый материал) Потенциальная энергия деформации: Внешние силы, приложенные к упругому телу, совершают работу. Обозначим её через А. В результате этой работы накапливается потенциальная энергия деформированного тела U. Кроме того, работа идёт на сообщение скорости массе тела, т.е. преобразуется в кинетическую энергию К. Баланс энергии имеет вид А = U + К. 20.Три стороны задачи определения напряжений при выводе формулы опр напр необходимо расм 3 стороны задачи 1) Геометрическая(ГС) устанавливает закон распределения деформации по сеч бруса 2) Физическая (ФС) связывает деформации с напр посредством закона Гука 3) Статическая сторона (СС) связ-ет напр с ВСФ(внутр сил фактор) посредствам зависимостей 21.Простое осевое растяжение – сжатие ГС 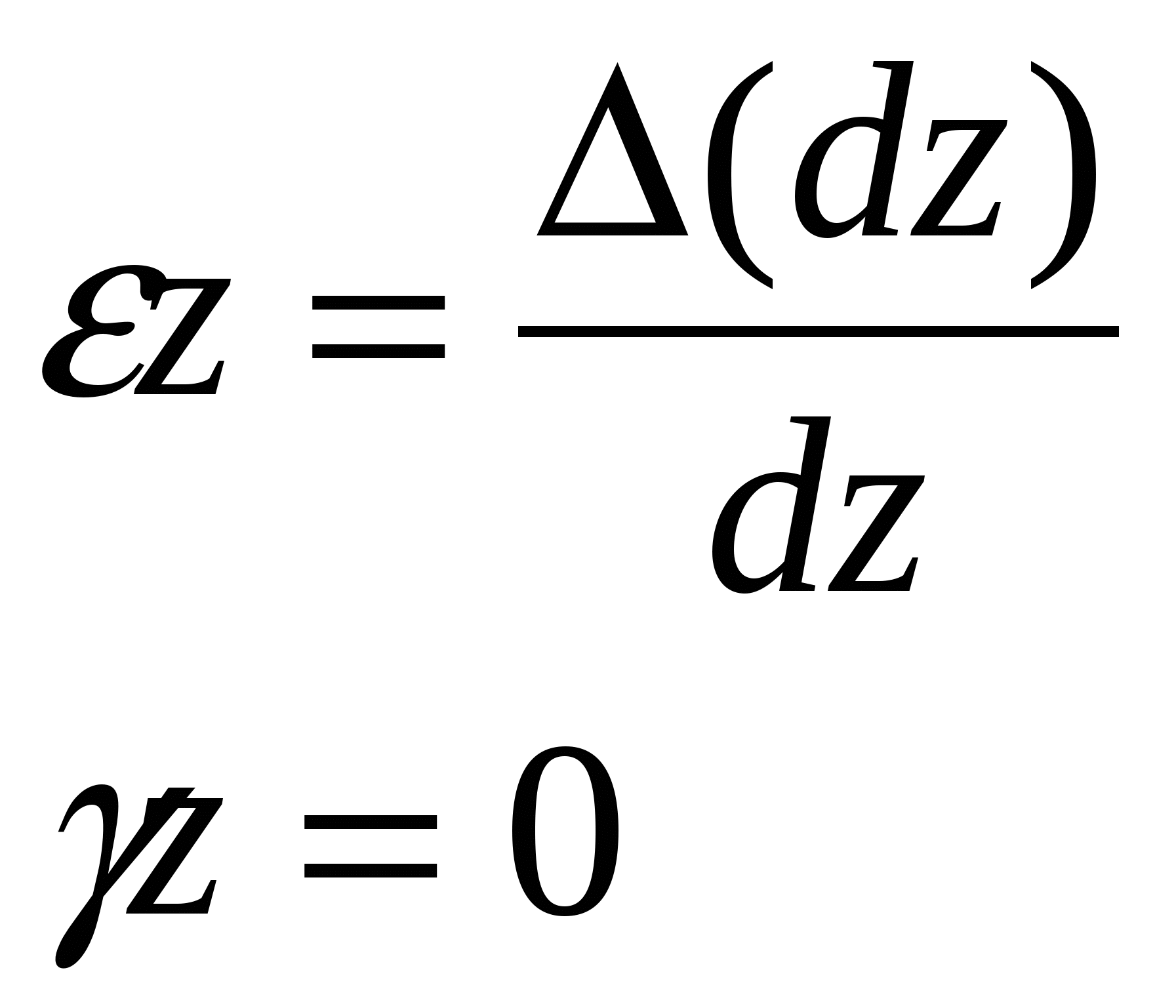 ФС 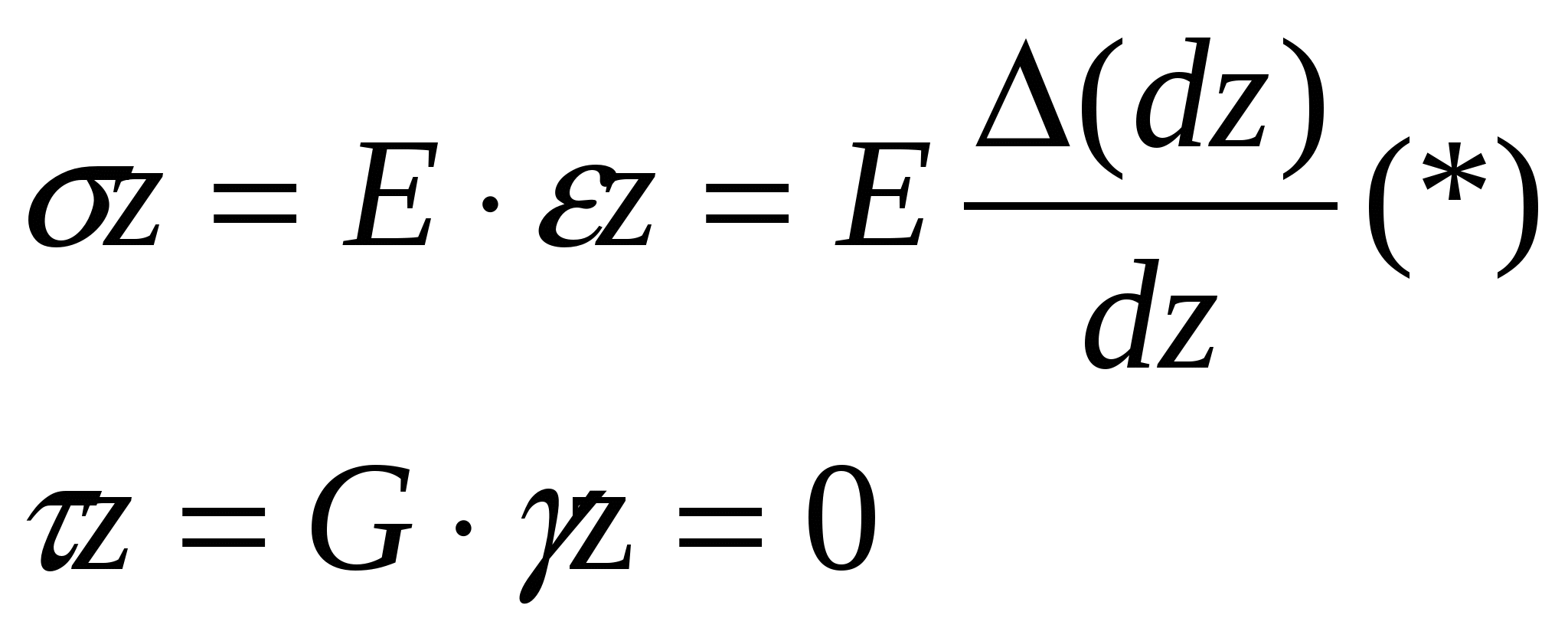 СС  из (*)и(**)  - ф-ла для определения напряжения раст-сжатии22.Формула для определения деформации бруса при растяжении-сжатии. Жесткость сечения бруса и физический смысл входящих в формулу величин Опр-е деформации бруса при раст-сжатии из (**)  l-длина бруса ЕА-жесткая сечение бруса при растяжении-сжатии 24.Формула для определения угла закручивания круглого бруса. Жесткость сечения бруса и физический смысл входящих в формулу величин из (**) 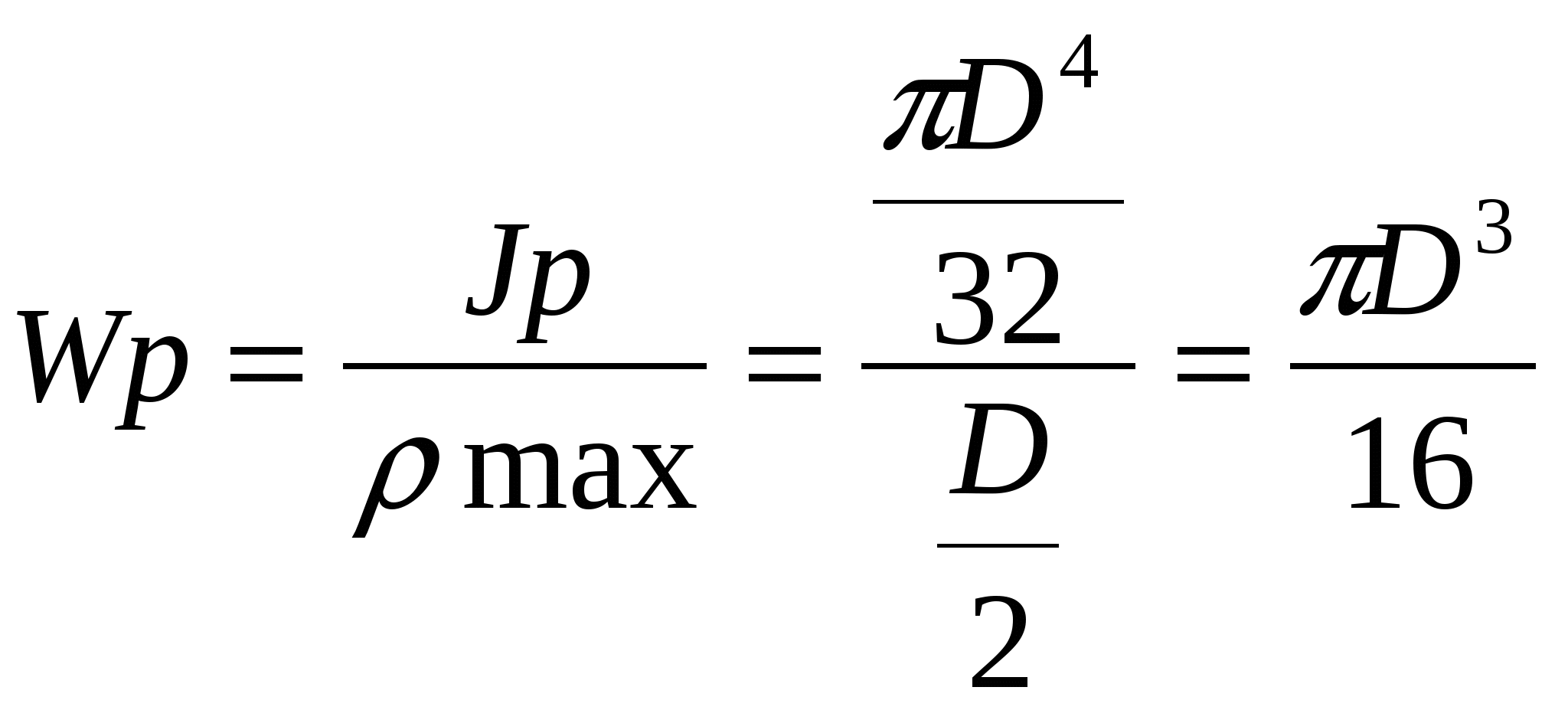   25.Кручение брусьев прямоугольного сечения  Wk- αhb^2 -момент сопротивления кручению Jk- βhb^3 –момент инерции при кручении для c h\b >10 α≈β≈1\3 т.о. Wk- 1\3 hb^2 26.Кручение тонкостенных стержней открытого и закрытого профиля Характерной геометрической особенностью тонкостенных стержней является то, что их толщина существенно (на порядок и более) меньше других геометрических размеров тонкостенное кольцо закрытого профиля 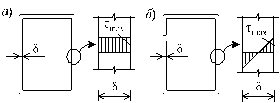     Характер распределения напряжений по толщине тонкостенного стержня открытого профиля близок к равномерному (рис. 4.7, б), а замкнутого профиля меняется по линейному закону, как это показано на рис. 4.7, а. Откуда следует, что напряжения в поперечных сечениях открытого профиля практически не изменятся, если профиль сечения распрямить. Иначе говоря, напряжения в криволинейном открытом профиле будут примерно такими же, как и в прямом. 27.Прямой чистый изгиб Все элементы конструкции подвергаются изгибу, они все рассчитываются на изгиб. При этом используют расчетную схему конструкции (наиболее распространенная расчетная схема для множества конструкций - балка на двух опорах). Балка – брус, который воспринимает поперечные нагрузки и работает на изгиб. Допущения при изгибе:
Чистый изгиб – когда в поперечных сечениях балки действует только изгибающий момент (частный случай). Поперечный изгиб – когда в поперечных сечениях действует одновременно и изгибающий момент и поперечная сила (общий случай).  Плоский (прямой) изгиб — когда изгибающий момент действует в плоскости, проходящей через одну из главных центральных осей инерции сечения, т.е. все силы лежат в плоскости симметрии балки. Основные гипотезы (допущения): гипотеза о не надавливании продольных волокон: волокна, параллельные оси балки, испытывают деформацию растяжения – сжатия и не оказывают давления друг на друга в поперечном направлении; гипотеза плоских сечений: сечение балки, плоское до деформации, остается плоским и нормальным к искривленной оси балки после деформации. При плоском изгибе в общем случае возникают внутренние силовые факторы: продольная сила N, поперечная сила Q и изгибающий момент М. N>0, если продольная сила растягивающая; при М>0 волокна сверху балки сжимаются, снизу растягиваются. .Слой, в котором отсутствуют удлинения, называется нейтральным слоем (осью, линией). При N=0 и Q=0, имеем случай чистого изгиба. Нормальные напряжения: , — радиус кривизны нейтрального слоя, y — расстояние от некоторого волокна до нейтрального слоя. Закон Гука при изгибе:  , откуда (формула Навье):  , Jx — момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости изгибающего момента, EJx — жесткость при изгибе,  — кривизна нейтрального слоя.Максимальные напряжения при изгибе возникают в точках, наиболее удаленных от нейтрального слоя:  , Jx/ymax=Wx—момент сопротивления сечения при изгибе,  . Если сечение не имеет горизонтальной оси симметрии, то эпюра нормальных напряжений не будет симметричной. Нейтральная ось сечения проходит через центр тяжести сечения. Формулы для определения нормального напряжения для чистого изгиба приближенно годятся и когда Q0. Это случай поперечного изгиба. При поперечном изгибе, кроме изгибающего момента М, действует поперечная сила Q и в сечении возникают не только нормальные , но и касательные напряжения. Касательные напряжения определяются формулой Журавского:  , где Sx(y) — статический момент относительно нейтральной оси той части площади, которая расположена ниже или выше слоя, отстоящего на расстоянии "y" от нейтральной оси; Jx — момент инерции всего поперечного сечения относительно нейтральной оси, b(y) — ширина сечения в слое, на котором определяются касательные напряжения. Для прямоугольного сечения:  , F=bh, для круглого сечения: , F=R2, для сечения любой формы  , k— коэфф., зависящий от формы сечения (прямоугольник: k= 1,5; круг - k= 1,33). 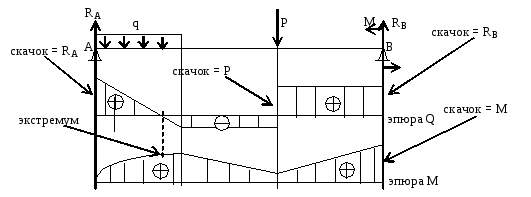 Mmax и Qmax определяются из эпюр изгибающих моментов и поперечных сил. Для этого балка разрезается на две части и рассматривается одна из них.  Действие отброшенной части заменяется внутренними силовыми факторами М и Q, которые определяются из уравнений равновесия. В некоторых вузах момент М>0 откладывается вниз, т.е. эпюра моментов строится на растянутых волокнах. При Q= 0 имеем экстремум эпюры моментов. Дифференциальные зависимости между М,Q и q:  q — интенсивность распределенной нагрузки [кН/м] Главные напряжения при поперечном изгибе:  .из (*)и(**)  -формула для вычисления норм напр при прямом чистом изгибе28.Понятие плоского поперечного изгиба. Расчетная формула для определения напряжений Чистый изгиб – вид нагружения, когда в поперечном сечении балки действует только изгибающий момент. Поперечный изгиб – когда на поперечное сечение действует одновременно изгибающий момент и поперечная сила (общий случай). Пример чистого изгиба:   - удельная нагрузка, приходящаяся на единицу длины конструкции.29.Определение касательных напряжений при плоском поперечном изгибе Касательные напряжения определяются формулой Журавского: 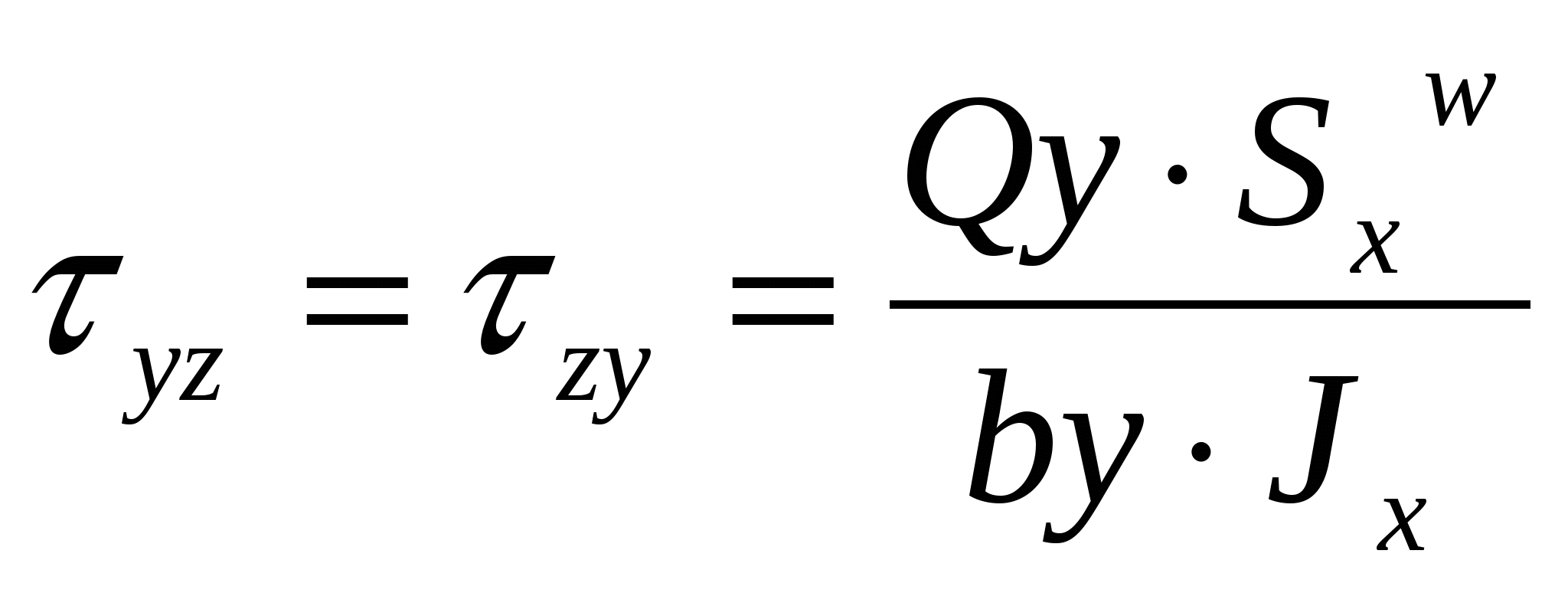 , где Qy-поперечная сила; Sx(y) — статический момент отсеченной части бруса относительно нейтральной оси той части площади, которая расположена ниже или выше слоя, отстоящего на расстоянии "y" от нейтральной оси; Jx — момент инерции всего поперечного сечения относительно нейтральной оси, b(y) — ширина сечения в слое, на котором определяются касательные напряжения.30.Распределение касательных напряжений в прямоугольном, двутавровом и швеллерном сечении а) прямоугольное сеч 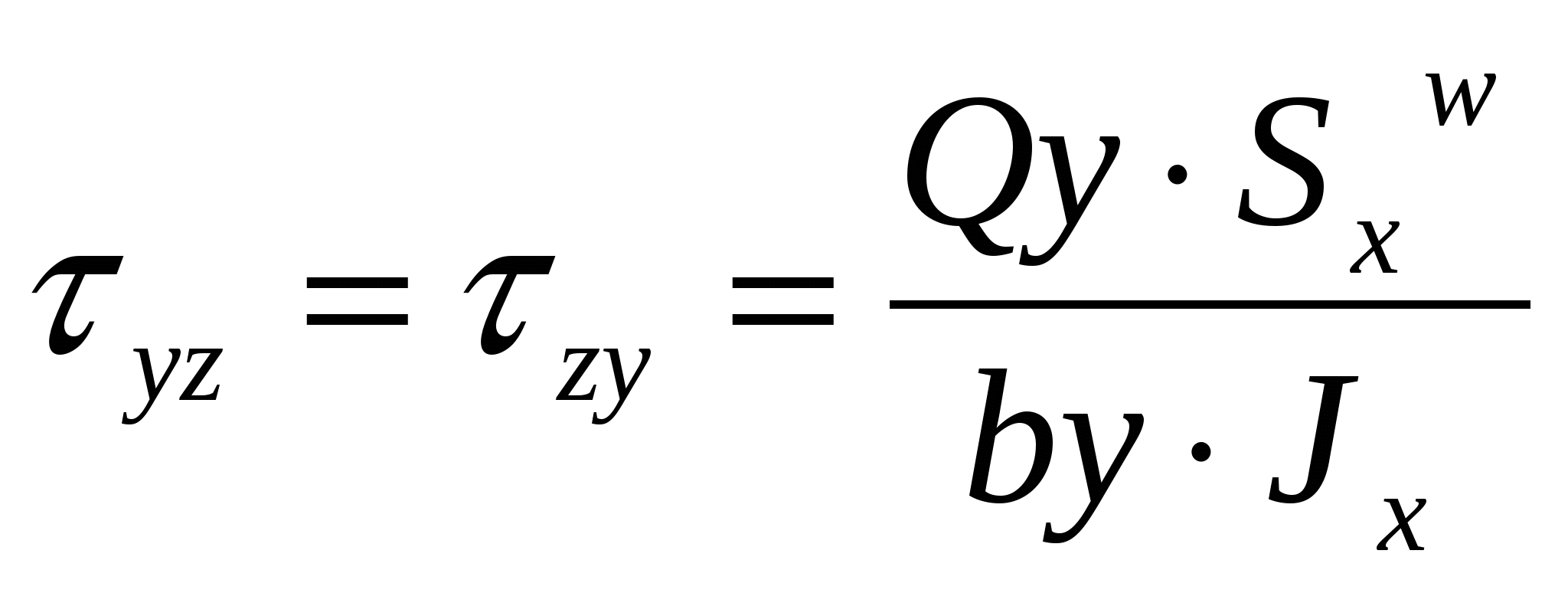 б) двутавровое сеч  г) швеллерное сеч 31.Роль касательных напряжений в балках, работающих на изгиб 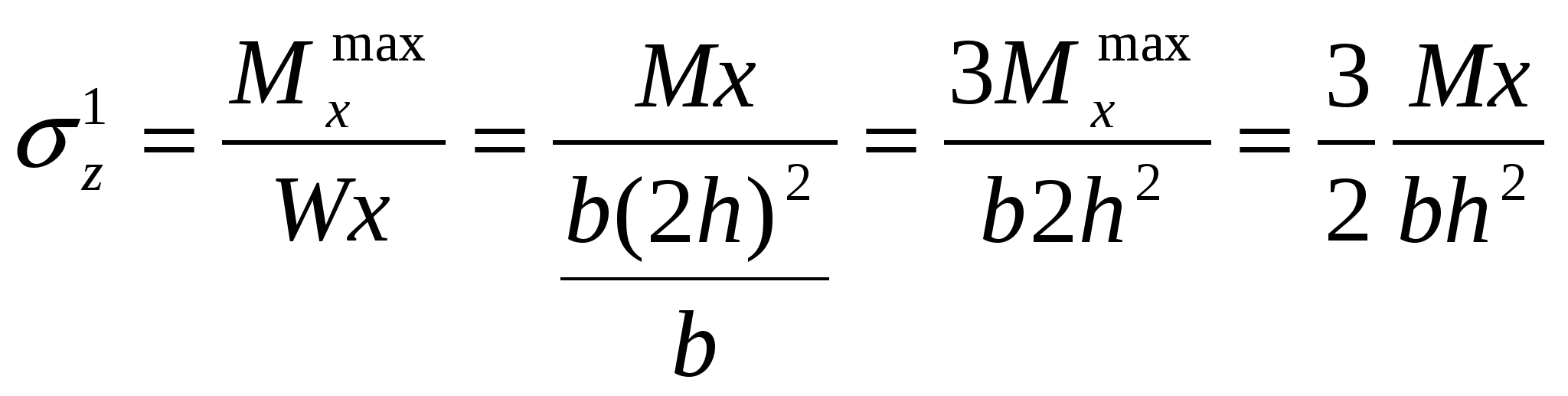 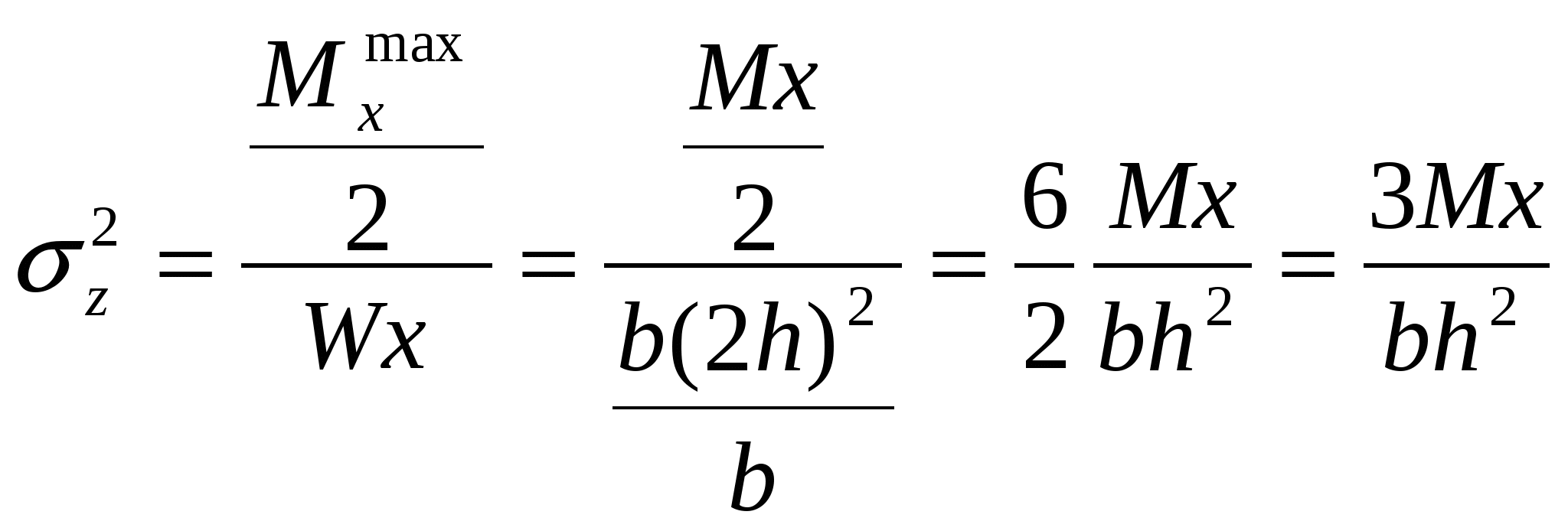 напряжение во 2 балке больше в 2 раза 32.Механические испытания материалов. Характеристики прочности материала По диаграмме растяжения оцениваются механические характеристики материала. 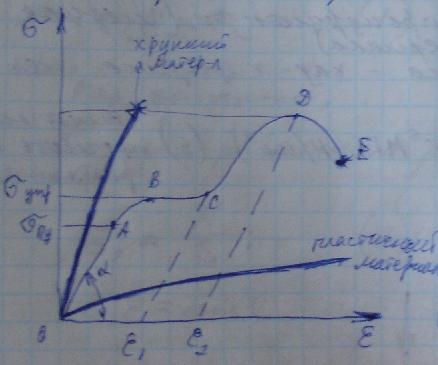 Деформация рассматривается для упругопластичного материала (малоуглеродистая сталь). т. А – предел пропорциональности  ;т. В – предел упругости  ;т. С – предел текучести  ;т. D – временный предел прочности; т. Е – разрушение образца. - это такое максимальное напряжение, до которого материал следует закону Гука. - такое максимальное напряжение, при котором после снятия нагрузки материал вернётся в исходное состояние. - это такое напряжение, при котором без видимого изменения нагрузки материал течёт. Если снимем нагрузку, материал вернётся в положение  .СD – зона упрочнения. Здесь удлинение образца сопровождается возрастанием нагрузки, но неизмеримо более медленным (в сотни раз), чем на упругом участке. т. D соответствует максимальному напряжению, при котором материал не разрушается. т. E – соответствует разрушению образца. tg  - даёт модуль упругости.Этот метод измерения характеристик материала самый простой, широкоиспользуемый и доступный. К основным механическим характеристикам материала относят пластичность, хрупкость и твёрдость. Способность материала без разрушения получать большие остаточные деформации носит название пластичности. Свойство пластичности имеет решающее значение для таких технологических операций, как штамповка, вытяжка, волочение, гибка и др. Мерой пластичности является удлинение  при разрыве. Чем больше , тем более пластичным считается материал.Свойством, противоположным пластичности, является хрупкость, т.е. способность материала разрушаться без образования заметных остаточных деформаций. Материалы, обладающие этим свойством, называются хрупкими. Диаграмма растяжения хрупких материалов не имеет площади текучести и зоны упрочнения. Под твёрдостью понимается способность материала противодействовать механическому проникновению в него посторонних тел. Наиболее широкое распространение получили методы измерения твёрдости по Бринеллю и по Роквеллу. а) Твёрдость по Бринеллю [НВ] – в поверхность исследуемой детали вдавливают стальной шарик диаметром 10 мм. б) Твёрдость по Роквеллу [HRC]– алмазный острый наконечник. В результате испытаний на твёрдость удаётся определить прочностные показатели материала, не разрушая деталь. Характеристики материалов: - Твёрдость; - Хрупкость; - Пластичность. Характеристиками пластичности материала являются относительное удлинение и относительное сужение при разрыве:   где l0, F0 — длина рабочей части образца и площадь поперечного сечения до деформации; lк — длина рабочей части образца после разрыва; F0 — конечная площадь поперечного сечения в шейке образца после разрыва. 34.Предельные и допускаемые напряжения При проектировании элемента конструкции необходимо определить размеры, обеспечивающие его безопасную работу при заданных нагрузках. Для успешного решения этой задачи необходимо исходить из того, чтобы наибольшее расчётное напряжение в поперечном сечении элемента конструкции, возникшее при заданной нагрузке, было меньше того предельного напряжения, при котором возникает опасность появления пластической деформации или опасность разрушения. Отношение предельного напряжения  к расчётному  называется коэффициентом запаса прочности s: .При расчёте элемента конструкции коэффициент запаса прочности задаётся заранее и называется нормативным или требуемым и обозначается [s]. Прочность элемента конструкции обеспечивается, если действительный коэффициент запаса прочности не ниже требуемого т.е. s>=[s] Это неравенство выражает условие прочности элемента конструкции. Разделив предельное напряжение на нормальный коэффициент запаса, получим допускаемое напряжение  : Тогда условие прочности можно выразить неравенством  т.е. прочность элемента конструкции обеспечивается, если наибольшее напряжение, возникающее в нём, не превышает допускаемого. 35.Три типа задач при расчетах на прочность. Примеры подбора поперечных сечений брусьев условия прочности при простейших деформациях
3 типа задач при расчете на прочность
пример опр размер поп сечения бруса квадр сеч. 1)эпюра     40. Определение главных напряжений в брусьях при растяжении-сжатии, кручении, изгибе 1) кручение (нсчс)   2) изгиб (лнс)   определив угол выбираем площадку с наиб. норм. напр. и поварачиваем ее на α против часовой стрелки | ||||||||||||||||||||||||||||||
;
