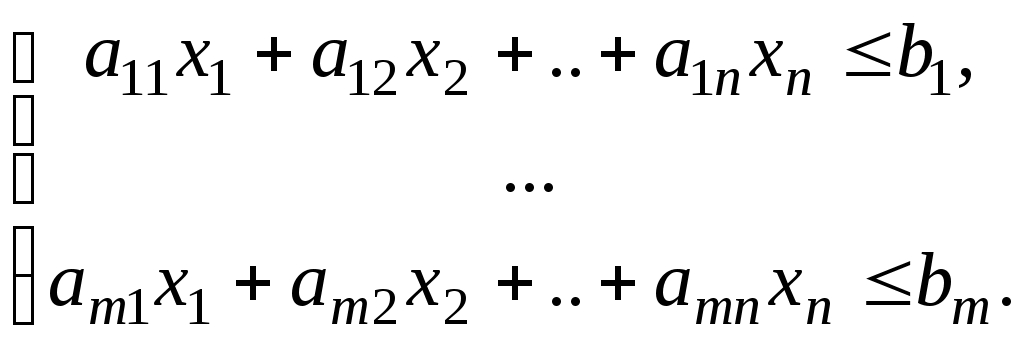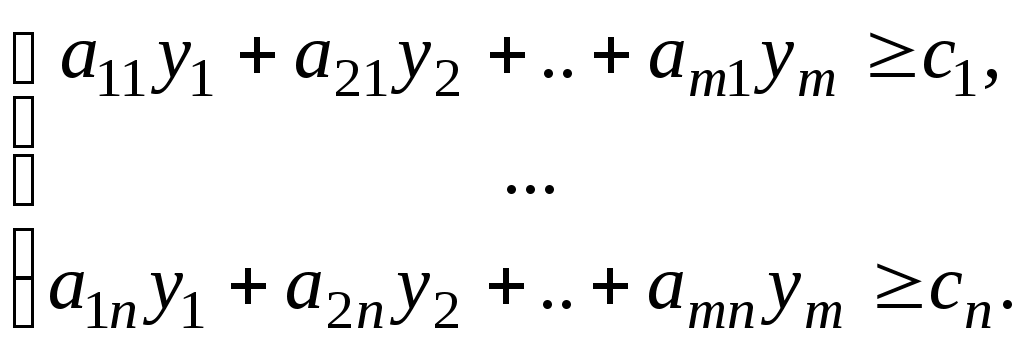Линейное программирование. 1. введение в линейное программирование

• Название: 1. введение в линейное программирование
• Анкор: Линейное программирование
• Дата: 12.04.2023
• Размер: 1.28 Mb.
• Имя файла: Topic1.doc
• Тип: Задача; #1057295
• страница: 4 из 6

1.4.Двойственная задача и ее решение

Каждой задаче линейного программирования можно определённым образом поставить в соответствие некоторую другую задачу линейного программирования, называемую сопряжённой или двойственной по отношению к исходной или прямой. Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей в нахождении максимального значения функции при ограничениях "с недостатком".

Две следующие задачи называются симметричными взаимно двойственными задачами линейного программирования:

Обе двойственные задачи линейного программирования обладают следующими свойствами:

1. 
   в одной задаче ищут максимум целевой функции, в другой  минимум;
   
2. 
   обе задачи являются стандартными задачами линейного программирования, причем в задаче о максимуме все неравенства вида "≤", а в задаче о минимуме  вида "≥" ;
   
3. 
   матрица системы ограничений одной задачи является транспонированной к матрице системы ограничений другой;
   
4. 
   коэффициенты при переменных целевой функции одной задачи являются свободными членами ограничений другой;
   
5. 
   число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче;
   
6. 
   условия неотрицательности имеются в обеих задачах.
   

Свойствами двойственных задач следует руководствоваться при их составлении.

1.5.Целочисленное программирование

Значительная часть задач по смыслу может иметь решения только в целых числах; например, число турбин, судов, животных может быть только целым числом. Такие задачи решаются методами целочисленного программирования. Общая постановка задачи линейного программирования дополняется требованием о том, чтобы найденные переменные в оптимальном плане были целыми.

Задачи целочисленного программирования решаются в Excel теми же средствами, что и общие задачи линейного программирования. В отличие от задач линейного программирования, при решении задач целочисленного программирования необходимо добавить указание на то, что разыскиваемые оптимальные значения переменных могут принимать только целые значения. Для этого в окне "Добавление ограничения" нужно выбрать в списке, расположенном посередине, значение "цел", как показано в следующем примере.

Пример 2.3. На мебельной фабрике изготавливают столы, стулья и табуреты. На производство одного изделия требуется 1,5, 1 и 0,62 м³ древесины. При этом затраты рабочего времени при изготовлении стола составляют 5 машино-часов, стула − 1,5 машино-часа и табурета − 0,7 машино-часа. Всего для производства мебели фабрика может ежедневно использовать 12 м³ древесины. Оборудование может быть занято в течение 26 машино-часов. Прибыль от реализации стола, стула и табуретки равна 200, 30 и 15 руб. соответственно. Фабрика должна ежедневно производить не менее двух столов. На производство другой продукции ограничений нет. Требуется определить, какую продукцию и в каком количестве следует ежедневно изготавливать фабрике, чтобы прибыль от ее реализации была максимальной.

Решение.

Составим вспомогательную таблицу:

	Стол	Стул	Табурет	Ограничение ресурсов
Древесина, м3	1,5	1	0,62	12
Рабочее время, маш.-час.	5	1,5	0,7	26
Прибыль за 1 шт., руб.	200	30	15

Определим переменные модели:

ежедневное производство столов (шт.);

ежедневное производство стульев (шт.);

ежедневное производство табуретов (шт.).

Используя эти переменные, далее строим целевую функцию:



Запишем ограничения:







Решение в Excel: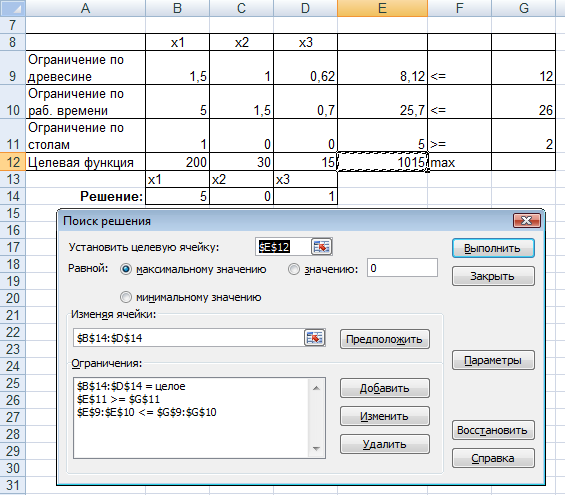



Рис. 2.4. Решение задачи целочисленного программирования