Линейное программирование. 1. введение в линейное программирование
 Скачать 1.28 Mb.
|
1.6.Симплекс-метод решения ЗЛПГрафический способ решения задачи ЛП показывает, что оптимальное решение этой задачи всегда ассоциируется с угловой точкой пространства решений (в математике она также называется крайней точкой множества). Это является ключевой идеей при разработке общего алгебраического симплекс-метода для решения любой задачи линейного программирования. Переход от геометрического способа решения задачи ЛП к симплекс-методу лежит через алгебраическое описание крайних точек пространства решений. Для реализации этого перехода сначала надо привести задачу ЛП к стандартной форме, преобразовав неравенства ограничений в равенства путем введения дополнительных переменных. Стандартная форма задачи ЛП необходима, потому что она позволяет получить базисное решение (используя систему уравнений, порожденную ограничениями). Это (алгебраическое) базисное решение полностью определяет все (геометрические) крайние точки пространства решений. Симплекс-метод позволяет эффективно найти оптимальное решение среди всех базисных. 1.6.1.Стандартная форма ЗЛПЗадача, в которой требуется найти экстремум функции  при ограничениях    называется задачей линейного программирования, заданной в канонической (стандартной) форме. Стандартная форма записи задачи ЛП предполагает выполнение следующих требований. Все ограничения (включая ограничения неотрицательности переменных) преобразуются в равенства с неотрицательной правой частью. Все переменные неотрицательные. Целевую функцию следует или максимизировать, или минимизировать. Преобразование неравенств в равенстваНеравенства любого типа (со знаками неравенств или ) можно преобразовать в равенства путем добавления в левую часть неравенств дополнительных (балансных) переменных – остаточных или избыточных, которые связаны с неравенствами типа «» или «» соответственно. Для неравенств типа «» в левую часть неравенства вводится неотрицательная переменная. Например, в модели компании Mikks, ограничение на количество сырья С1 задается в идее неравенства  . Вводя новую неотрицательную переменную  , которая показывает остаток (неиспользованное количество) сырья С1, это ограничение преобразуется в равенство   Неравенства типа «≥» в задачах ЛП обычно устанавливают нижнюю границу чего-либо. Избыточная переменная определяет превышение значения левой части неравенства над этой границей. Так, в модели «диеты» неравенство  показывает, что суточное производство пищевой добавки не должно быть меньше 800 фунтов. Математически это неравенство эквивалентно равенству  ,  .Положительное значение избыточной переменной показывает превышение суточного производства добавки над минимальным значением 800 фунтов.Пример 2.4. Преобразуем следующую задачу ЛП в стандартную форму:  при выполнении следующих условий:     Для преобразования задачи в стандартную форму выполним следующие действия. Вычтем из левой части первого неравенства дополнительную (избыточную) переменную  и затем умножим все неравенство на -1, для того чтобы правая часть неравенства стала положительной. Добавим дополнительную (остаточную) переменную  клевой части второго неравенства.Так как третье ограничение изначально записано в виде равенства, поэтому оставляем его без изменения. Получаем следующую стандартную задачу линейного программирования.  при выполнении следующих условий:     1.6.2.Основы симплекс-методаРассмотрим общую ЗЛП с 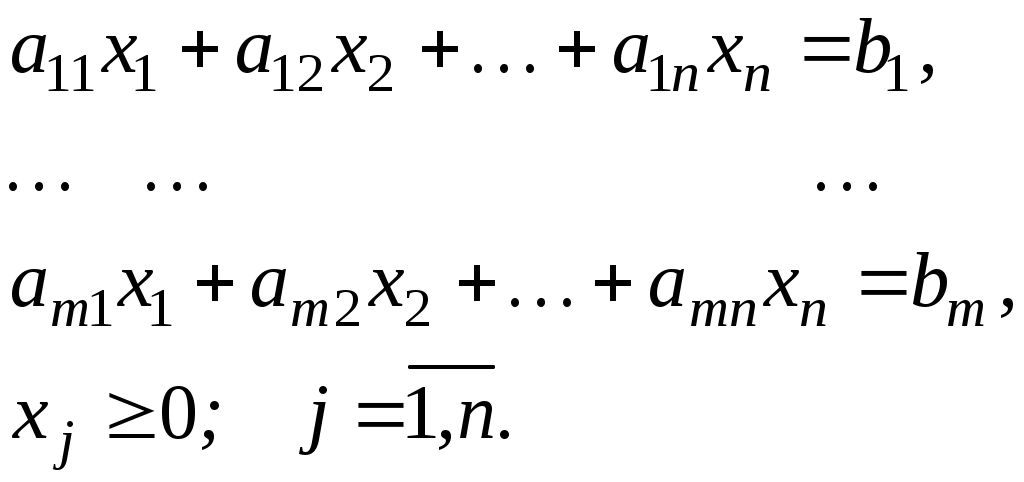 ограничениями и  переменными, записанную в стандартной (канонической) форме , (2.1)Как правило, число уравнений задачи меньше числа переменных (т.е.  ), поэтому множество ее допустимых решений равно  . Задача состоит в том, чтобы найти наилучшее решение в смысле принятого критерия (минимума целевой функции).Мы уже говорили, что оптимальное решение представляет собой одну из вершин многогранника допустимой области. Другими словами, оптимальное решение это одно из базисных решений. Получение одного из базисных решений основано на известном классическом методе решения систем линейных уравнений – методе Гаусса-Жордана. Основная идея этого метода состоит в сведении системы уравнений с  неизвестными к каноническому или ступенчатому виду при помощи элементарных операций над строками:умножение любого уравнения системы на положительное или отрицательное число; прибавление к любому уравнению другого уравнения системы, умноженного на положительное или отрицательное число. При использовании первых 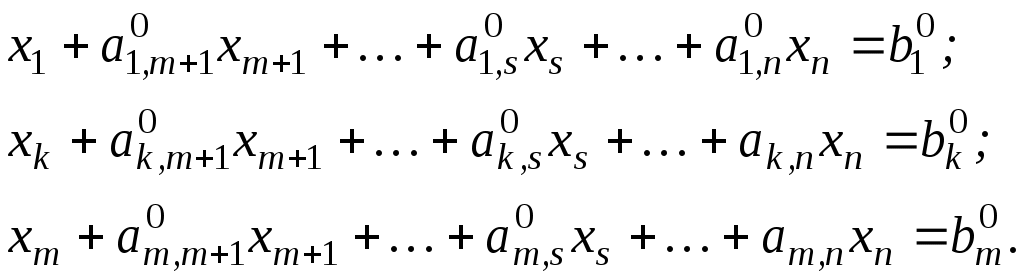переменных такая система имеет следующий вид: (2.2)Переменные  , входящие с единичными коэффициентами в одно уравнение системы (2.2) и с нулевыми в остальные, называются базисными. В канонической системе каждому уравнению соответствует ровно одна базисная переменная.Остальные  переменные  называются небазисными переменными.При записи системы в каноническом виде все ее решения можно получить, присваивая независимым переменным произвольные значения и решая затем получающуюся систему относительно базисных переменных. Определение. Базисным решением системы (2.2) называется решение, полученное при нулевых значениях небазисных переменных. Например, в системе (2.2) одно из базисных решений задается как 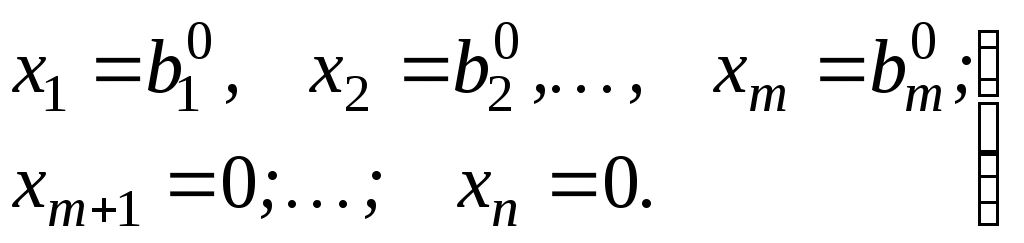 (2.3)Определение. Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных  , что эквивалентно условию  .Т.к. различные базисные решения системы (2.2) соответствуют различным вариантам выбора  из общего числа  переменных  , то число допустимых базисных решений (угловых точек) не превышает  .Поэтому ЗЛП можно решать посредством перебора конечного числа угловых точек допустимого множества  , сравнивая значения ЦФ в этих точках. Это наихудший вариант решения ЗЛП, т.к. требует огромного объема вычислений.Пример: если  (задача небольшой размерности), то количество переборов составит  (кол-во вариантов). Обычно  .Идея симплекс-метода (СМ) состоит в направленном переборе угловых точек допустимого множества с последовательным уменьшением ЦФ  . СМ разработал Дж. Данциг (американский ученый) в 1947 г. Этот метод называют также методом последовательного улучшения решения (плана). Гарантии результативности СМ обеспечиваются следующей теоремой.Теорема (о конечности алгоритма симплекс-метода). Если существует оптимальное решение ЗЛП, то существует и базисное оптимальное решение. Это решение может быть получено через конечное число шагов симплекс-методом, причем, начать можно с любого исходного базиса. 1.6.3.Вычислительный алгоритм симплекс-методаРассмотрим работу алгоритма на примере компании Mikks. Приведем еще раз ее математическую модель:  при выполнении следующих ограничений:      ,  .Эта задача в стандартной форме записывается так:  при выполнении следующих ограничений:      Здесь  дополнительные (остаточные) переменные, добавленные в неравенства для преобразования их в равенства.Ручные вычисления по симплекс-методу удобно оформлять в виде так называемых симплекс-таблиц (СТ).
Замечание. Если целевую функцию необходимо максимизировать, то предварительно нужно умножить ее на (–1). Сформулируем алгоритм СМ применительно к данным, внесенным в таблице. Шаг 1. Выяснить, имеются ли в последней строке таблицы отрицательные числа (значение в последнем столбце не принимается во внимание). Если все числа неотрицательны, то процесс закончен; базисное решение  является оптимальным;  .Если в последней строке имеются отрицательные числа, перейти к Шагу 2. Шаг 2. Просмотреть столбец, соответствующий наименьшему отрицательному числу и выяснить, имеются ли в нем положительные числа. Если ни в одном из таких столбцов нет положительных чисел, то оптимального решения не существует. Если найден столбец, содержащий хотя бы один положительный элемент, отметить его и перейти к Шагу 3. Шаг 3. Разделить свободные члены на соответствующие положительные числа из выделенного столбца и выбрать наименьшее частное. Отметить строку, соответствующую наименьшему частному (горизонтальной стрелкой). Выделить разрешающий элемент  , стоящий на пересечении отмеченных строки и столбца. Перейти к Шагу 4.Шаг 4. Поменять местами переменные  и , остальные переменные оставить на прежних местах.На место опорного элемента поставить число  .На остальных местах разрешающей (опорной) строки записать соответствующие элементы исходной таблицы, делённые на опорный элемент. На свободные места разрешающего столбца поставить со знаком минус соответствующие элементы исходной таблицы, делённые на опорный элемент. Шаг 5. Оставшиеся свободные места в новой СТ заполнить построчно следующим образом: из строки элементов исходной таблицы вычесть произведение ее элемента из разрешающего столбца на уже заполненную разрешающую строку новой таблицы. На этом заполнение новой таблицы заканчивается и происходит переход к Шагу 1. Пример 2.5. Приведем ход решения задачи по данному алгоритму:
Ответ:  |
