3 вариант. 1. Задание 1 407953
 Скачать 134.93 Kb.
|
|
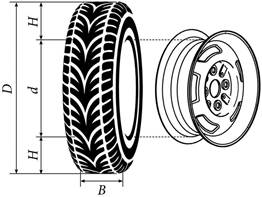
1. Задание 1 № 407953 Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
Шины какой наименьшей ширины можно устанавливать на автомобиль, если диаметр диска равен 15 дюймам? Ответ дайте в миллиметрах.
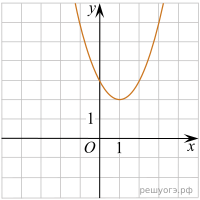
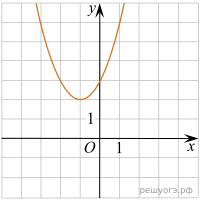
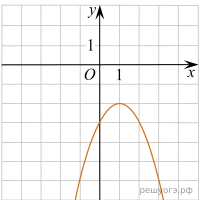
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине. Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рисунке 2). Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины (параметр на рисунке 2) к ширине шины, то есть  Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции. За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры. Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 165/70 R13. 2. Задание 2 № 407955 На сколько миллиметров радиус колеса с шиной маркировки 205/55 R14 больше, чем радиус колеса с шиной маркировки 165/65 R14? 3. Задание 3 № 408171 На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 195/50 R15? 4. Задание 4 № 408172 Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах. 5. Задание 5 № 408173 На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 175/60 R14? Результат округлите до десятых. 6. Задание 6 № 348647 Найдите значение выражения  .7. Задание 7 № 339306 На координатной прямой отмечены числа a и b. В ответе укажите номер правильного варианта.  Какое из следующих утверждений относительно этих чисел является верным? 1) a3>0 2) a − b > 0 3) ab < 1 4) a + b > 1 8. Задание 8 № 311383 Найдите значение выражения  при  9. Задание 9 № 311755 Решите уравнение  10. Задание 10 № 132730 Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет. 11. Задание 11 № 193093 На одном из рисунков изображен график функции  . Укажите номер этого рисунка.
12. Задание 12 № 46 Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле  , где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.13. Задание 13 № 351881 Решите неравенство  1) [-8;8] 2)  3) нет решений 4)  14. Задание 14 № 393958 Компания «Альфа» начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания «Бета» начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10 000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась? 15. Задание 15 № 322819 Катеты прямоугольного треугольника равны 35 и 120. Найдите высоту, проведенную к гипотенузе. 16. Задание 16 № 356359  Радиус вписанной в квадрат окружности равен  Найдите радиус окружности, описанной около этого квадрата.17. Задание 17 № 169863  Периметр квадрата равен 40. Найдите площадь квадрата.18. Задание 18 № 340589 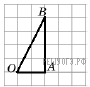 Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.19. Задание 19 № 67 Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы равны. 3) Любая биссектриса равнобедренного треугольника является его медианой. Если утверждений несколько, запишите их номера в порядке возрастания. 20. Задание 20 № 311582 Упростите выражение:  .21. Задание 21 № 338961 Первую половину трассы автомобиль проехал со скоростью 55 км/ч, а вторую — со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. 22. Задание 22 № 338253 Постройте график функции  и определите, при каких значениях m прямая  имеет с графиком ровно три общие точки.23. Задание 23 № 311706 Высота треугольника разбивает его основание на два отрезка с длинами 8 и 9. Найдите длину этой высоты, если известно, что другая высота треугольника делит ее пополам. 24. Задание 24 № 333026 Точка E — середина боковой стороны AB трапеции ABCD. Докажите, что площадь треугольника ECD равна половине площади трапеции. 25. Задание 25 № 311252 Стороны AC, AB, BC треугольника ABC равны  соответственно. Точка K расположена вне треугольника ABC, причем отрезок KC пересекает отрезок AB в точке, отличной от  Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если  Ключ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
