Математикалық есептер шығару практикумы. 12 Ибатова А.С. Мат есептер шыг практикумы. 12. Нктелерді геометриялы орны (нго) дісі. Нго ымы. арапайым нго. Нго іздеу. Нго дісімен шешілетін геометриялы салулара мысалдар. Инверсия дісі
 Скачать 1.92 Mb. Скачать 1.92 Mb.
|
|
12. Нүктелердің геометриялық орны (НГО) әдісі. НГО ұғымы. Қарапайым НГО. НГО іздеу. НГО әдісімен шешілетін геометриялық салуларға мысалдар. Инверсия әдісі. 12.1. Нүктелердің геометриялық орыны әдісі. Геометриялық орын түсінігі айтарлықтай әдістемелік және білім беру мәніне ие. Оның жазықтықтағы бейнеленуінен кеңістікте кескінделуі дамуындағы орынын бағалау қиын. Геометриялық орын әдістері қолданылатын есептерді шешуде кеңістікте алдымен жеңілірек, одан кейін қиындау геометриялық денелердің қатынастарын орнату ыңғайлы. Нүктелердің геометриялық орыны — басқа әр түрлі денелердің қиылысуы, беттесуі немесе олардың тіпті ортақ нүктесі болмауы мүмкін. Нүктелердің геометриялық орыны деп бірнеше қасиеттерге ие болатын нүктелердің жиынтығын айтамыз. Жазықтықта тек нүктелердің геометриялық орыны деп қарастырсақ, ал кеңістікте сонымен қатар түзулердің (түзу және қисық) де геометриялық орынын қарастыруға болады. Сондықтан кеңістікте геометриялық орын дегеніміз — орны бір немесе бірнеше нақты шарттарды қанағаттандыратын көптеген элементтердің жиыны. Бұл жерде «нүкте» сөзінің орынына тек нүкте емес, түзуден де тұратын кең мағыналы «элемент» сөзі қолданылып тұр. 12.2. НГО ұғымы. Геометриялық денелер әртүрлі тәсілмен берілуі мүмкін. Денелердің қиылысуы немесе бірігуі түрінде, оның қасиеттерін анықтайтын нұсқау арқылы, оның әр нүктелерінің қасиеттері арқылы да тағы басқа түрде берілуі мүмкін. Мысалы: Кез-келген АВ кесіндісін былай беруге болады (1-сурет): 1) AM және BN сәулелерінің қиылысуы; 2) 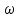 шеңберінің диаметрі; 3) l түзуіне параллель шеңберінің диаметрі; 3) l түзуіне параллель 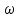 шеңберінің барлық хордаларының орталарының жиынтығы, және тағы басқа. шеңберінің барлық хордаларының орталарының жиынтығы, және тағы басқа. 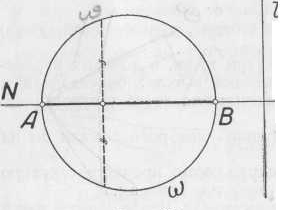 1-сурет. Егер дене тек қана осы денеге тиісті нүктелердің қасиеттерімен берілген болса, онда бұл дене —нүктелердің геометриялық орыны деп аталады. Бұдан берілген қасиеттерге ие болатын жазықтықтағы нүктелердің және тек қана осы нүктелерден құралған нүктелердің геометриялық орыны –дене деп аталады. Біздің мысалда АВ кесіндісі l түзуіне параллель болатын 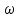 шеңберінің хордаларының орталарының геометриялық орыны болып табылады. Осы немесе басқа да нүктелердің геометриялық орынымінезделетін қасиет осы нүктелердің геометриялық орынының характеристикалык қасиеті деп аталады. шеңберінің хордаларының орталарының геометриялық орыны болып табылады. Осы немесе басқа да нүктелердің геометриялық орынымінезделетін қасиет осы нүктелердің геометриялық орынының характеристикалык қасиеті деп аталады.Геометриялық денелер геометрияға жаңадан көбінде тек осы геометриялық орын ретінде енгізіледі. Мысалға шеңбер — мектептегі геометрия курсында, эллипс, гипербала және парабала — аналитикалық геометрия курсында. Аналитикалық геометрияда сызықтардың теңдеулерін құруда оларды нүктелердің геометриялық орыны ретінде қарастырады. Нүктелердің геометриялық орыны тек қана сызық немесе бірнеше сызықтардың бірігуінен ғана емес, сонымен қатар нүктелердің ақырғы жиынтығы , жазықтықтардың ауданы және тағы басқа. Кейде тіпті бірнеше аталған қасиеттерге ие болатын нүктелердің геометриялық орыны мүлде болмайтын жағдай болады.Ф – дене аталған қасиеттерге ие болатын бұл нүктелердің геометриялық орыны екенін дәлелдеу үшін өзара кері мына екі сөйлемді дәлелдеу керек болады: Ф – дененің әр нүктесі бұл қасиеттерге ие. Аталған қасиеттерге ие болатын әр нүкте Ф денеге тиісті. 12.3. Қарапайым НГО. Жазықтықтағы өте қарапайым нүктелердің геометриялық орыны мектепте геометрия курсында қарастырылады. Біз осылардың ең қажеттілерін қарастырайық. 1. О нүктесінен r қашықтықта жататын нүктелердің геометриялық орыны— бұл радиусы r, центрі О нүктесі болатын шеңбер болады. 2. Берілген екі нүктеден де бірдей қашықтықта жататын нүктелердің геометриялық орыны — бұл осы екі нүктені қосатын кесіндінің ортасынан өтетін және осы түзуге перпендикуляр болатын екінші бір түзуді береді. Бұл нүктелердің геометриялық орыны кейде берілген нүктелердің симметриалі немесе медиатриссасы деп аталады(2-сурет).  2-cурет. 3. Берілген түзуден h қашықтықта орналасқан нүктелердің геометриялық орыны — берілген түзуге параллель түзулердің пары болып табылады. Бұл нүктелердің геометриялық орынын салу үшін а түзуінен кез- келген А нүктесін алып, сол нүктеден 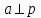 болатындай р түзуін жүргіземіз. Енді а түзуінің екі жағынан да бірдей h қашықтықта а түзуіне параллель болатындай р түзуін жүргіземіз. Енді а түзуінің екі жағынан да бірдей h қашықтықта а түзуіне параллель 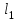 және және 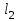 түзуін жүргіземіз(3-сурет). түзуін жүргіземіз(3-сурет).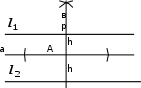 3-сурет. 4. Екі параллель түзуден бірдей арақашықтықтағы нүктелердің геометриялық орыны— бұл берілген екі түзуге параллель түзу болып табылады. Бұл геометриялық орыны салу үшін а және в параллель түзулерін қиятын с түзуін жүргіземіз. Осы кесіндінің ортасын тауып, сол нүктеден а және в түзулеріне параллель болатындай l түзуін жүргіземіз. Кейде бұл түзу берілген параллель екі түзудің ортаңғы түзуі деп те аталады(4-сурет).  4-сурет. 5. Қиылысатын екі түзуден бірдей қашықтықтағы нүктелердің геометриялық орыны — өзара перпендикуляр екі түзуді береді. Бұл түзулер берілген екі түзуден жасалған бұрыштардың биссектрисасы болып табылады(5-сурет).  5-cурет. 12.4. НГО іздеу. Қандайда бір қасиетке ие болатын нүктелердің геометриялық орыны табыңыз – деген тапсырмалар практикада жиі кездеседі. Мұндай тапсырмалардың негізгі тоқтамы бірнеше «қарапайым» немесе «элементар» денелер жиынтығы белгіленіп алынғанын ұйғарады. Мұнда жиынтықтағы қай дене өзінен ізделінді геометриялық орынды көрсететінін табу керек. Бұл үшін алдын – ала белгілі, қарапайым, элементар болып есептелетін барлық денелердің тізімін құру қажет. Бұл тізім шартты болып табылады. Элементар планиметрия шарттарында белгілі болғандай элементар денелер қатарына мына денелерді жатқызамыз: барлық жазықтықтар, нүктелер, түзулер, кесінділер, сәулелер, шеңберлер, шеңбер доғалары.егер қандай да бір денелер екі элементар денелердің қиылысуы, бірігуі немесе айырымы болса, онда оларды да элементар денелердің қатарына жатқызамыз. Бұл тізім элементар денелер класын анықтайды. Бұл денелердің қатарына кез-келген нүктелердің жиынтығы, әртүрлі көпбұрыштар, дөңгелек, дөңгелекті сегмент, сектор, екі параллель түзудің арасындағы жолақ, жартылай жазықтықтар да кіреді. Берілген қасиеттерге ие болатын нүктелердің геометриялық орынын табу туралы тапсырманың нақты мағынасы ізделінді нүктелердің геометриялық орыны дәл қай элементар дене екенін көрсету үшін құрылған. Нүктелердің геометриялық орынын табуға арналған тапсырмаларды шешу әдетте анализ жасауға, дәлелдеуге негізделеді. Бұл геометрияда салу есептеріне ұқсас. Бірақ нүктелердің геометриялық орынын табуды оны салумен алмастыруға болмайды. Кейде нүктелердің геометриялық орыны табылып және берілген құралдармен салыну мүмкін емес болады. Анализ жасаудың мақсаты — ізделінді нүктелердің геометриялық орыны не болып табылатынына байланысты бірнеше гипотезалар жасау. Анализ жасау әдетте чертежда берілген денені салады және болжам жасап қандай да бір ізделінді нүктелердің геометриялық орынына тиісті нүктені қарастырудан басталады. Бұл нүкте мен нүктелердің геометриялық орынының анықтамасынан шығатын және оның формасы мен жағдайын анықтауға көмектесетін берілген элементтермен бірнеше байланыстар жасайды. Кейде анализ жасауға қандай да бір жеке жағдайлар немесе ізделінді геометриялық орынға тиісті бірнеше нүктелердің өзіндік салынуы да себеп болады. Анализ қорытындысында есептің шешуіне біз тек қана болжалды жауап береміз. Оны ары қарай айқындап немесе дәлелдеу керек. Дәлелдеу барысында екі өзара кері сөйлемдерді түсінеміз: 1) Анализ жасауда табылған дененің барлық нүктелері ізделінді нүктелердің геометриялық орынындағы нүктенің характеристикалық қасиеттеріне ие. 2) Характеристикалық қасиеттеріне ие барлық нүктелер анализ жасауда табылған денеге тиісті. (2) сөйлемді дәлелдеу келесі сөйлемді дәлелдеумен алмастырылуы мүмкін екенін де білу керек:  ) Егер қандай да бір нүкте табылған денеге тиісті емес болса, онда ол нүкте характеристикалық қасиетке ие бола алмайды. Бұл сөйлемнің бірі анализ жасау барысында-ақ жиі қолданылатынын байқауға болады. ) Егер қандай да бір нүкте табылған денеге тиісті емес болса, онда ол нүкте характеристикалық қасиетке ие бола алмайды. Бұл сөйлемнің бірі анализ жасау барысында-ақ жиі қолданылатынын байқауға болады.Зерттеу есепті шешу барысында мүмкін пайда болатын, осы немесе басқа да берілгендерді таңдауға байланысты әртүрлі жағдайларды қарастырумен қорытындыланады. 12.5. НГО әдісімен шешілетін геометриялық салуларға мысалдар. Кеңістіктегі негізгі геометриялық орындар. Қарапайым геометрия курсында және өмірде де кездесетін геометриялық орындарды көрсетейік. Геометриялық орындардың тізімі шексіз көп екеніне көз жеткіземіз. Енді осы айтылған кеңістіктегі нүктелердің геометриялық орындарының біразын қарастырайық: I.О нүктесінен бірдей а қашықтықта жатқан нүктелердің геометриялық орыны— центрі О нүктесі және радиусы а болатын сфера болады(6-сурет). 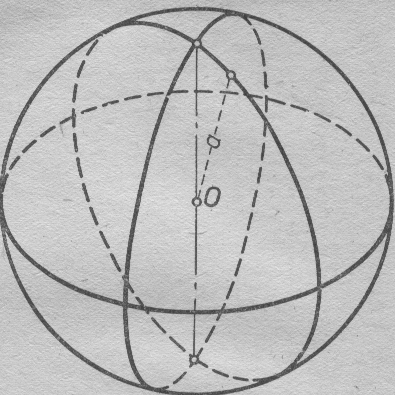 1-сурет. 6-сурет. II.в түзуінен бірдей а қащықтықта жатқан нүктелердің геометриялық орыны — цилиндрлік бет болады. в түзуі оның осі, ал бағыттаушы шеңбердің радиусы – а, бұл жазықтық оське перпендикуляр болады. I 2-сурет. II. 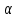 жазықтығынан а қашықтықта жатқан екі параллель жазықтықтар болады(7-сурет). жазықтығынан а қашықтықта жатқан екі параллель жазықтықтар болады(7-сурет).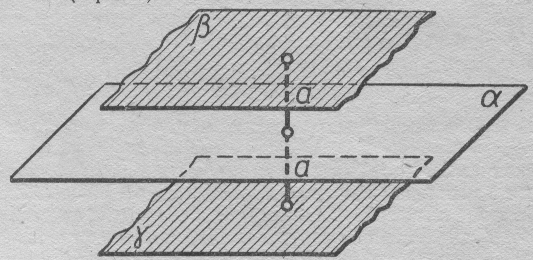 7-сурет. IV.А және В нүктелерінен бірдей қашықтықта жатқан нүктелердің геометриялық орыны — АВ кесіндісінің ортасында орналасып және осы кесіндіге перпендикуляр болатын 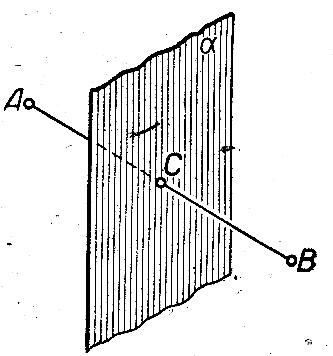 8-сурет. V.Екі түзуден бірдей арақашықтықта жатқан нүктелердің геометриялық орыны. Екі түзу кеңістікте параллель орналасуы, қиылысуы немесе айқасуы мүмкін екенін біз білеміз. Осыған байланысты нүктелердің геометриялық орыны әр жағдайда әртүрлі формаға ие болады. а) а және в түзулері қиылысады. қиылысатын екі түзуден бірдей қашықтықта жатқан нүктелердің геометриялық орыны — екі өзара перпендикуляр болатын б) а және в түзулері параллель. Мұнда түзулерден бірдей арақашықтықта нүктелердің геометриялық орыны — а, в түзулеріне параллель, с ортаңғы түзуінен өтетін және сол 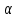 жазықтығына перпендикуляр болатын жазықтығына перпендикуляр болатын 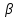 жазықтығын береді(9-сурет). жазықтығын береді(9-сурет).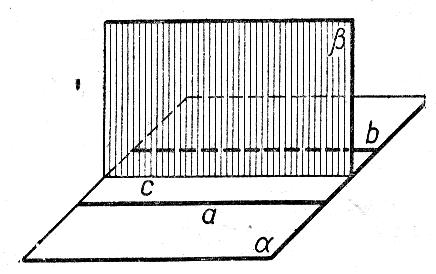 9-сурет. в) а және в түзулері айқасады. Мұндай жағдайда нүктелердің геометриялық орыны бір немесе екі жазықтықтар болмайды, онда ол күрделі формаға ие болады. Бұл геометриялық орындардың қасиеттерін анықтау үшін былай талқылаймыз: а және в түзулері айқасқан түзулерін с түзуімен қиамыз. Сонда а және с қиылысқан түзулерден бірдей арақашықтықта жатқан нүктелердің геометриялық орыны — 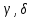 екі жазықтығы болады. Біруақытта екі жазықтығы болады. Біруақытта 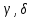 жазықтығына да тиісті нүктелер а,в және с түзулерінен бірдей қашықтықта болады, сондықтан жазықтығына да тиісті нүктелер а,в және с түзулерінен бірдей қашықтықта болады, сондықтан 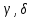 жазықтығымен қиылысқандағы төрт түзу ізделінді нүктелердің геометриялық орынын береді. жазықтығымен қиылысқандағы төрт түзу ізделінді нүктелердің геометриялық орынын береді. Енді а және в айқас түзулерін қиятын 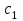 түзуін жүргізейік. Жоғарыдағыдай талқылай отырып, біз тағы да ізделінді геометриялық орынға тиісті төрт түзуді аламыз. түзуін жүргізейік. Жоғарыдағыдай талқылай отырып, біз тағы да ізделінді геометриялық орынға тиісті төрт түзуді аламыз.Осылайша бірдей қашықтықта жататын шексіз көп түзулерді алуға болады. бұл түзулердің барлығы да бір бетте жатады. Бұл бетті осы түзулердің тұғыры деп қарастыруға болады, сондықтан а және в айқасқан түзулерінен бірдей қашықтықта жататын нүктелердің геометриялық орыны — қандайда бір түзу сызықты бет болады. бұл бет гипербалалық парабалоид деп аталады және ер тәрізді формада болады(10-сурет). Бұл гипербалалық парабалоид екеніне бұл беттің аналитикалық теңдеуін декарттық координатаға салу арқылы көз жеткізуге болады. Біз барлық геометриялық орынды қарастырмай, тек қана бірнеше жай ғана алынған түзулерден құрылған бөлігін қараймыз және оларды шартты түрде а, в түзулерінен бірдей қашықтықта жатқан нүктелердің геометриялық орыны деп есептеймсіз. 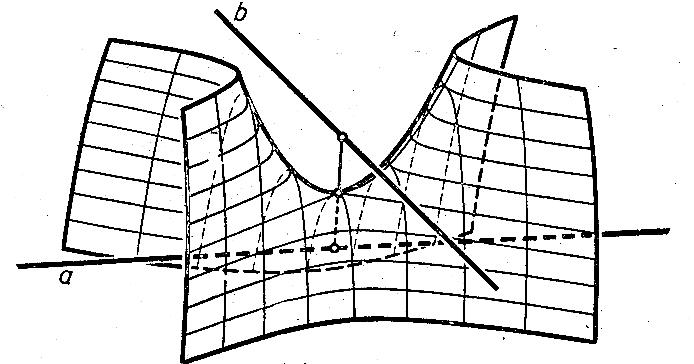 10-сурет. VI., қиылысатын екі жазықтықтан бірдей қашықтықта жататын нүктелердің геометриялық орыны –осы жазықтықтармен жасалған екі жақты бұрыштарды қақ бөлетін екі өзара перпендикуляр және жазықтықтарын береді(11-сурет). 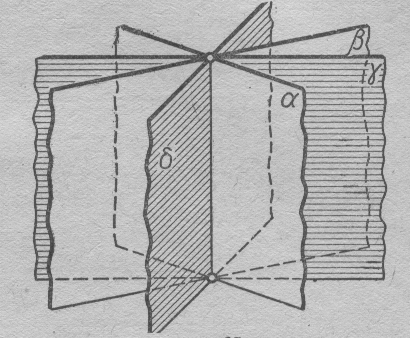 11-сурет. VII. Үш нүктеден бірдей қашықтықта жатқан нүктелердің геометриялық орыны . Мұнда 2 жағдай мүмкін: а)Берілген А, В және С нүктелері бір түзудің бойында жатпайды. Бұл жағдайда ізделінді геометриялық орын – берілген үш нүктеден анықталған ж 7-сурет. азықтыққа перпендикуляр болатын АВС үшбұрышының әр қабырғасының ортасына жүргізілген перпендикуляр түзудің қиылысу нүктесі арқылы өтетін а түзуі болып табылады. Бұл түзу АВ, АС, ВСтүзулерінің ортасы арқылы өтетін және оларға перпендикуляр орналасқан үш жазықтықтың қиылысу сызығы болады (12-сурет). 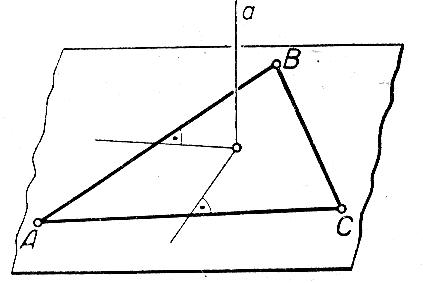 12-сурет. Екінші ретті беттер нүктенің геометриялық орыны ретінде. Кеңістікке геометриялық орындар туралы айтқанда, ІІ-ретті беттерді нүктенің және түзулердің геометриялық орыны ретінде қарастырмауға болмайды. Екінші ретті беттер аналитикалық геометрияда кең түрде оқытылады. Тікбұрышты координаттық жүйеде олардың теңдеуі екінші дәрежелі болғандықтан екінші ретті беттер деп аталады. Бұл беттер мыналар: шар, эллипсоид, бірқуысты және екіқуысты гиперболоидтар, эллипстік және гиперболалық параболоидтар, конустық және цилиндрлік беттер. Осы тізімдегі кейбір беттер туралы біз жоғарғыда кездестіргенбіз. Мысалы: сфера (І, ХІ, XIV,XV, XVI, XVIII г.о.), конустық бет (XII, XIII г.о.), цилиндрлік бет (II г.о.), гиперболалық параболоид (V, в.г.о.). Берілген нүктеге дейінгі және берілген түзуге дейінгі арақашықтық қатынасы е – тұрақты мәнге ие болатын, жазықтықтағы екінші ретті қисықтардың нүктелердің геометриялық орыны ретінде анықтамасы белгілі. е<1 болғанда эллипс, е=1 болғанда парабола және е>1 болғанда гипербола болады. Осыған ұқсас ІІ-ретті беттерге де анықтама беруге болады. Кеңістіктен қандай да бір Ғ нүктесін және осы нүктеден өтпейтін α жазықтығын аламыз. Кеңістіктегі нүктелердің Ғ нүктеге дейінгі және α жазықтыққа дейінгі қашықтықтарды салыстырамыз. Сонда келесі жағдайдын дұрыс екенін көрсетуге болады. Ғ нүктесіне дейінгі арақашықтардың берілген α жазықтыққа дейінгі арақашықтығына қатынасы е тұрақтысы болатын кеңістіктегі нүктелердің геометриялық орыны е<1 болғанда сығылған айналмалы эллипсоид, е>1 болғанда айналмалы екіқуысты гиперболоид және е=1 болғанда айналмалы параболоид болады. Дәлелдеу үшін Ғ нүктесі арқылы α жазықтығына перпендикуляр болатын қандай да бір β жазықтығын жүргізейік. β жазықтығы α жазықтығымен d түзуі арқылы қиылысады (25-сурет). β жазықтығы Ғ нүктесіне дейінгі және d түзуіне дейінгі арақашықтықтың қатынасы тұрақты е-ге тең нүктелердің геометриялық орыны болатын қисық жатады. Жоғарыда айтылған бұл қисық е<1 болғанда эллипс, е>1 болғанда гипербола және е=1 болғанда парабола болатыны белгілі. Ғ нүктесі бұл қисық үшін фокус, ал d түзуі – директрисса болады. Енді Ғ нүктесі арқылы қандай да бір басқа α жазықтығымен d1 түзуі арқылы қиылысатын β1жазықтығын жүргіземіз. Бұл β жазықтығында да Ғ нүктесіне дейінгі арақашықтықтың d1 түзуіне дейінгі арақашықтыққа қатынасы е тұрақтыға тең нүктелердің геометриялық орыны болатын қисық бар. Мұнда да Ғ нүктесі бұл қисық үшін фокус, ал d1 түзуі – директриса болады. β1 жазықтығы қисық β жазықтығындағы қисыққа конгруэнтті және α жазықтығы β және β1 жазықтықтары арасындағы бұрышпен тең бұрышқа Ғ нүктеге түсірілген ҒК перпендикулярынан айналасына β жазықтығындағы қисығын бұру арқылы алынуы мүмкін. Ғ нүктесі арқылы β2, β3..., жазықтықтар жүргізе отырып, олардың әрқайсындағы қисық β жазықтығы қисыққа конгруэнтті болады деп қорытындылаймыз және ҒК перпендикулярының айналасына сәйкес бұрышы арқылы бұрып алынуы мүмкін. β, β1,β2,..., жазықтықтары пайда болған қисықтарды, ізделінді геометриялық орнының осы ҒК арқылы өтетін жазықтығымен қиылысу ретінде қарастыруға болады. Қиылысуда конгруэнтті қисықтар болғандықтан, ізделінді геометриялық орны айнымалы бет болады. Мұндағы ҒК осы беттің айналу осі болады. Егер β жазықтығын ҒК бойынша айналдырсақ, онда d түзуі α жазықтығын салады, ал β жазықтығы қисық (эллипс, гипербола немесе парабола, е мәніне тәуелді) қандай да бір айналмалы ІІ-ретті бетті береді. Біз е мәніне тәуелді айналмалы эллипсоид, екіқуысты гиперболоид және параболоид аламыз. Бұлар ізделінді геометриялық орындарды анықтайды. Сонымен жоғарыда келтірілген беттердің нүктелердің гегометриялық орны ретінде берілген анықтамасы ІІ-ретті беттердің тек қана жеке түрлерін береді, ол – айнымалы беттер. Егер нүктенлердің жазықтыққа дейінгі арақашықтығын нақты арақашықтық ретінде емес, нақты бір бағыт бойынша арақашықтық деп ұқсақ, онда ІІ-ретті беттердің жалпы түрін алуға болады. Ғ нүктесі арқылы α жазықтығына перпендикуляр емес, параллель де емес, қандай да бір а түзуін жүргізейік және кез келген М нүктесінен α жазықтығына дейінгі арақашықтықты а түзуіне параллель түзу арқылы өлшейміз, оны М нүктесінен α жазықтығына дейінгі қиғаш арақашықтық деп атаймыз. Бұл жағдайда біз айналу беттерін емес, беттердің жалпы түрлерін аламыз, дәлірек айтқанда: е<1 боланда эллипсоид, е=1 болғанда эллипстік парабола, е>1 болғанда екіқуысты гиперболоид. Егер берілген Ғ нүктесі α жазықтығында жатса, онда геометриялық орыны басқа формаға ие болады. Бұл осі Ғ нүктесінен өтетін α жазықтығына перпендикуляр болатын конустық бет болады (ХІІІ, в.г.о.). Екінші ретті беттерді нүктенің геометриялық орыны ретінде және басқа да жолмен алуға болады. Тағы да ІІ-ретті қисықтардың анықтамасын жазықтықта нүктелердің геометриялық орыны ретінде аламыз, бұлардың берілген нүктеден және берілген түзуден қашықтықтарының қатынасы е тұрақты мәнге ие болады. е<1 боланда эллипс, е>1 болғанда гипербола және е=1 болғанда парабола аламыз. Егер біз нүктелердің геометриялық орнын жазықтықта емес, кеңістікте қарастырсақ, онда барлық ІІ-ретті беттерді алуға болады. Берілген Ғ нүктесіне дейінгі және берілген d... түзуіне дейінгі қашықтықтардың қатынасы е тұрақты мәнге ие болатын кеңістіктегі М нүктелердің геометриялық орыны - е<1 боланда сығылған айнымалы эллипсоид, е>1 болғанда сығылған айнымалы бірқуысты гиперболоид және е=1 болғанда параболалық цилиндр болады. Енді біз d түзуі және оған да, d-ға параллель емес α жазықтығына да тиісті емес, М нүктесін алайық (28-сурет). М нүктесінен d түзуіне дейінгі арақашықтықты перпендикуляр бойынша емес, α-ға параллель түзу арқылы өлшейміз. Осы α жазықтығына параллель және d-ға тиісті N нүктесі мен М нүктесін қосатын кесіндіні М нүктесінен d түзуіне дейінгі бағыттаушы аралық дейміз, ал, α - бағыттаушы жазықтық. Егер басында α жазықтық d түзуін және Ғ нүктесі анықталған жазықтыққа перпендикуляр деп жорысақ, онда келесі сөйлемдер дұрыс. Егер кеңістікте d түзуі, оған жатпайын Ғ нүктесі және осы нүкте мен d түзуі анықталған жазықтыққа перпендикуляр екінші ретті бет болады. α бағыттаушы жазықтық берілсе, онда Ғ нүктесіне дейінгі арақашықтықтың d түзуіне дейінгі бағыттаушы аралыққа қатынасы тұрақты е болатын: МҒ:МN=е. Егер d түзуімен бағыттауыш α жазықтығының арасындағы бұрышты деп алсақ, онда бет мынадай болады: е Бұл анықтамалардың ішінде біз жоғарыдағы (v,в) кездескен гиперболалық парабалоид қана жоқ. Мысал 1: Төбесіндегі бұрышы, табаны және іштей сызылған шеңбердің радиусы берілген. Үшбұрыш салу керек. Анализ:  ізделінді үшбұрыш, ізделінді үшбұрыш, 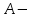 оның берілген бұрышы, оның берілген бұрышы, 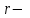 іштей сызылған шеңбердің радиусы, іштей сызылған шеңбердің радиусы, 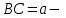 табаны. табаны.Іштей сызылған шеңбердің О – центрін қарастырамыз. О нүктесінің 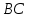 түзуінен қашықтығы түзуінен қашықтығы 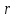 (центрдің бірінші қасиеті). (центрдің бірінші қасиеті).Бұдан басқа ( 13-сурет), 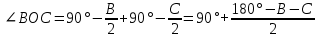 Сондықтан 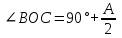 (центрдің екінші қасиеті). (центрдің екінші қасиеті).Бірінші қасиетке ие болатын НГО 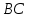 түзуіне параллель түзулер жұбын береді. Екінші қасиетке ие болатын НГО ( түзуіне параллель түзулер жұбын береді. Екінші қасиетке ие болатын НГО (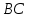 түзуі О нүктеден түзуі О нүктеден 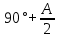 бұрышпен көрінеді), бұрышпен көрінеді), 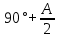 бұрыш жасайтын сегменттің доғалар жұбын береді. Бұл екі геометриялық орындардың әр қиылысу нүктелері іштей сызылған шеңбердің центрі қызметін атқарады. бұрыш жасайтын сегменттің доғалар жұбын береді. Бұл екі геометриялық орындардың әр қиылысу нүктелері іштей сызылған шеңбердің центрі қызметін атқарады.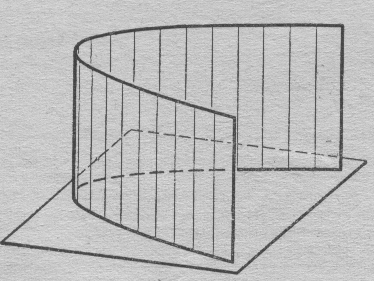 13-сурет Салу: Кез-келген түзуден 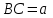 кесіндісін өлшеп аламыз; кесіндісін өлшеп аламыз;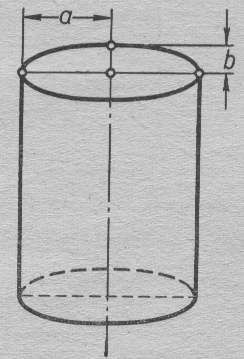 14-сурет 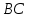 түзуіне парллель және одан бірдей қашықтықта жататын түзуіне парллель және одан бірдей қашықтықта жататын 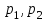 түзулер жұбын саламыз; түзулер жұбын саламыз;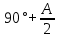 бұрыш жаайтын сегменттер жұбын саламыз; бұрыш жаайтын сегменттер жұбын саламыз;Айтылған геометриялық орындардың геометрилық орындары ретінде О нүктесін аламыз; 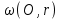 шеңберлерін саламыз; шеңберлерін саламыз;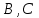 нүктелерінен нүктелерінен 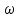 шеңберіне жанасатындай шеңберіне жанасатындай 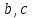 сәулелерін жүргіземіз; сәулелерін жүргіземіз;Бұл сәулелердің қиылысуын 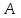 деп белгілейміз. деп белгілейміз. 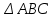 - ізделінді үшбұрыш. - ізделінді үшбұрыш.Зерттеу: Жоғарыда айтылған екі геометриялық орындардың қиылысу нүктелері табылу үшін қажетті және жеткілікті шарты сегмент ұшының r кесіндісінен кіші болуы, яғни мына теңсіздіктің орындалуы: 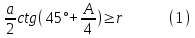 5,6,7 - қадамдар әрқашан орынды. Соңғы мынадан шығады: 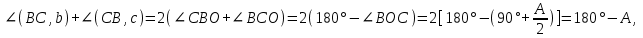 Сондықтан Сондықтан 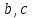 сәулелері мүмкін болатын ұқсас төрт шешімнің арасындағы айырмашылықты қарастырмай-ақ қиылысатынын көреміз (О нүктесін алуымызға байланысты); сәулелері мүмкін болатын ұқсас төрт шешімнің арасындағы айырмашылықты қарастырмай-ақ қиылысатынын көреміз (О нүктесін алуымызға байланысты);Келесідей қорытынды жасауға болады: (1)шарты бойынша есптің жалғыз шешімі болады, ал егер бұл шарт орындалмаса есептің шешімі болмайды. 12.6. Инверсия әдісі. Салу есептерін шешудің тағы бір әдісі – инверсия әдісі. Бұл әдістің көмегімен әлдеқайда қиынырақ салу есептері шешіледі. Инверсия әдісі басқа әдістерге қарағанда кейінірек пайда болған және оның қиындығы – көп салулар орындау қажеттілігінде. Айталық жазықтықта w (О, R) шеңбері берілген. Анықтама: Жазықтықтың О нүктесінен өзге кез – келген Р нүктесіне мына шарттарды: 1) Р' Î [ОР) 2) ОР × ОР' = R2 қанағаттандыратындай Р' нүктесін сәйкес қоятын жазықтық түрлендіруін инверсия деп атайды (15-сурет). 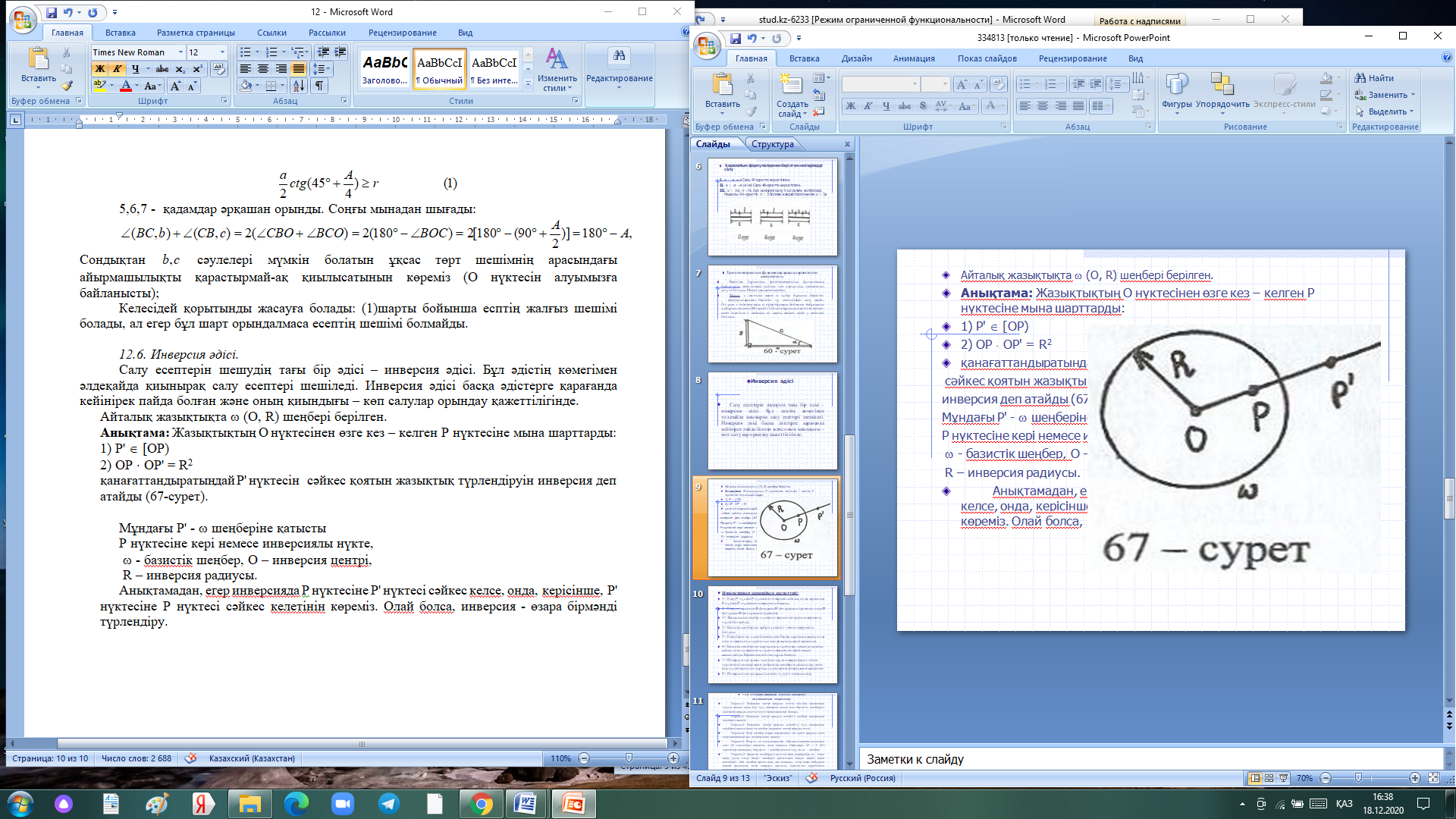 15-сурет Мұндағы Р' - w шеңберіне қатысты Р нүктесіне кері немесе инверсиялы нүкте, w - базистік шеңбер, О – инверсия центрі, R – инверсия радиусы. Анықтамадан, егер инверсияда Р нүктесіне Р' нүктесі сәйкес келсе, онда, керісінше, Р' нүктесіне Р нүктесі сәйкес келетінін көреміз. Олай болса, инверсия - өзара бірмәнді түрлендіру. Инверсияның қарапайым қасиеттері: 10. Егер Р' нүктесі Р нүктесіне инверсиялы болса, онда, керісінше, Р нүктесі Р' нүктесіне инверсиялы болады. 20. Егер инверсияда Ф фигурасы Ф' фигурасына түрленсе, онда Ф' фигурасы Ф фигурасына түрленеді. 30. Жазықтықтың ешбір нүктесі инверсия центріне инверсиялы нүкте болмайды. 40. Базистік шеңбердің әрбір нүктесі өз - өзіне инверсиялы болады. 50. Егер берілген нүкте базистік шеңбердің сыртында жатса, онда оған инверсиялы нүкте оның ішінде жатады және керісінше. 60. Базистік шеңбердің сыртындағы нүкте одан шексіз алыстаған сайын, оған инверсиялы нүкте инверсия центріне шексіз жақындайды. Керісінше сөйлем дұрыс болады. 70. Инверсия центрінен шығатын сәуле инверсияда өз - өзіне түрленеді (көшеді) және де базистік шеңберге қатысты сәуленің ішкі нүктелері оның сыртқы нүктелеріне көшеді және керісінше. 80. Инверсия центрі арқылы өтетін түзу өз - өзіне көшеді. Салу есептерін инверсия әдісімен шешкенде қолданылатын теоремалар Теорема1: Инверсия центрі арқылы өтетін шеңбер инверсияда түзуге көшеді және бұл түзу инверсия центрі мен берілген шеңбердің центрлері арқылы өтетін түзуге перпендикуляр болады. Теорема2: Инверсия центрі арқылы өтпейтін шеңбер инверсияда шеңберге көшеді. Теорема3: Инверсия центрі арқылы өтпейтін түзу инверсияда шеңберге көшеді және ол шеңбер инверсия центрі арқылы өтеді. Теорема4: Егер шеңбер өзара инверсиялы екі нүкте арқылы өтсе, онда инверсияда бұл шеңбер өзіне көшеді. Теорема5: Егер w1, w2 сызықтары бір – бірінен инверсия центрінен өзге М нүктесінде жанасса, онда олардың образдары М' = f (М) нүктесінде жанасады. Мұнда w1 – шеңбер немесе түзу, ал w2 – шеңбер. Теорема 6: Базистік шеңберден өзге шеңбер инверсияда өз - өзіне көшу үшін, оның базис шеңберге ортогональ болуы қажет және жеткілікті. (Екі шеңбер ортогональ деп аталады, егер олар тікбұрыш жасай қиылысса, яғни олардың қиылысу нүктесінен жүргізілген радиустары өзара перпендикуляр болса.) ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ Шарыгин И.Ф., Бүкүбаева К.О. Геометрия. 10-11 сынып. Жалпы білім беретін мектерге арналған оқулық. – Алматы.: «Кітап баспасы», 2008. 448 бет. А.В.Погорелов., Геометрия.7-11. Алматы: Рауан. 2010ж. 384 бет. Мусин А.Т. Геометрия негіздемелері. Көкшетау: 2008ж Гусев В. Геометрия 11-сынып. Алматы. 2007ж Геометрия [Текст] : жалпы білім беретін мектеп.7-9 сынып.арналған оқулық / Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. 2ші бас. Алматы : Мектеп, 2011. 334б. с. : Юсупов, Ж. Геометрия [Текст] : жалпы білім беретін орта мектептің 8сыныбына арн. оқулық / Ж. Юсупов, С. С. Зәуірбеков. Алматы : Мектеп, 2004. 86 б. |
