шпоры по статистике. 12. средние величины, способы их расчета

• Название: 12. средние величины, способы их расчета
• Анкор: шпоры по статистике
• Дата: 05.05.2022
• Размер: 284.14 Kb.
• Имя файла: шпоры по статистике.docx
• Тип: Закон; #514175
• страница: 1 из 4

12. средние величины, способы их расчета

Средняя величина - это обобщающий показатель статистической совокупности, который погашает индивидуальные различия значений статистических величин, позволяя сравнивать разные совокупности между собой.

Средние величины – обобщающие показатели, в которых находят выражение действие общих условий, закономерность изучаемого явления.

При помощи средних происходит сглаживание различий в величине признака, которые возникают по тем или иным причинам у отдельных единиц наблюдения. Средние имеют те же единицы измерения, что и признаки, по которым они вычисляются.

Средние величины используются на этапе обработки и обобщения полученных первичных статистических данных. Потребность определения средних величин связана с тем, что у различных единиц исследуемых совокупностей индивидуальные значения одного и того же признака, как правило, неодинаковы. При исследовании совокупности с качественно разнородными признаками на первый план может выступить нетипичность средних показателей. Такими, к примеру, являются средние показатели произведенного национального дохода на душу населения (разные возрастные группы), средние показатели урожайности зерновых культур по всей территории России (районы разных климатических зон и разных зерновых культур), средние показатели рождаемости населения по всем регионам страны, средние температуры за определенный период и т.д. Различные средние выводятся из общей формулы степенной средней: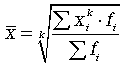


Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1.

Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1: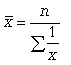

 (5.6)

Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000). Существуют формулы для простой и взвешенной средней геометрической.

Для  простой сре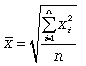дней геометрической

Для  взвешенной средней геометрической  (5.9)

Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения).

Формула  простой средней квадратической

 (5.10)

Формула 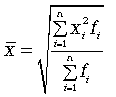 взвешенной средней квадратической

 (5.11)

Правило мажорантности средних: чем выше показатель степени m, тем больше величина средней.
13.мода и медиана, методика расчета

Мода (Mo) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой, т.е. мода – значение признака, встречающееся чаще всего.

Определение моды по дискретному вариационному ряду: наибольшую частоту (60 человек) имеет 5-й тарифный разряд, следовательно, он и является модальным. Mo = 5.

В отличие от дискретных вариационных рядов определение моды по интервальным рядам требует проведения определенных расчетов на основе следующих формул:
, (6)
где x₀ – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);
i – величина модального интервала;
f_Mo – частота модального интервала;
f_Mo-1 – частота интервала, предшествующего модальному;
f_Mo+1 – частота интервала, следующего за модальным.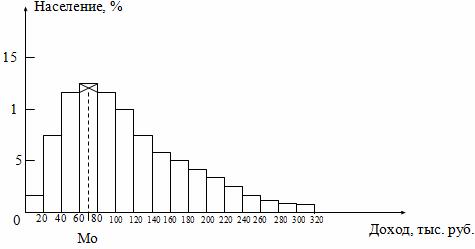



Выбирается самый высокий прямоугольник. Затем правую вершину соединяем с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Из точки их пересечения опускаем перпендикуляр на ось абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения

Медиана. Медиана   вариационного ряда* – это значение, которая делит его на две равные части (по количеству вариант).

* не важно, дискретного или интервального, генеральной совокупности или выборочной.

Медиану можно отыскать несколькими способами.

Если даны первичные данные, то сортируем их по возрастанию либо убыванию (см. Задание 1) и находим середину ранжированного ряда:  . Почему именно 13-е число? Потому что перед ним находится 12 чисел и после него тоже 12 чисел, таким образом, значение   разделило ряд на две равные части, а значит, является медианой. Этот номер можно найти аналитически:

– если совокупность содержит нечётное количество чисел (наш случай), то делим её объём пополам:   и округляем полученное значение в большую сторону: 13 – получая тем самым срединный номер.

– если совокупность содержит чётное количество чисел, например, 20, то делаем то же самое: 20/2=10, и медианное значение здесь рассчитывается как среднее арифметическое 10-го и следующего числа:  .
14.ряды динамики, их виды и особенности

Динамический интервальный ряд содержит значения показателей за определенные периоды времени. В интервальном ряду уровни можно суммировать, получая объем явления за более длительный период, или так называемые накопленные итоги.

Ряд динамический моментныйДинамический моментный ряд отражает значения показателей на определенный момент времени (дату времени). В моментных рядах исследователя может интересовать только разность явлений, отражающая изменение уровня ряда между определенными датами, поскольку сумма уровней здесь не имеет реального содержания. Накопленные итоги здесь не рассчитываются.

Важнейшим условием правильного построения динамических рядов является Сопоставимость уровней динамических рядовсопоставимость уровней рядов, относящихся к различным периодам. Уровни должны быть представлены в однородных величинах, должна иметь место одинаковая полнота охвата различных частей явления.

Для того, чтобы избежать искажения реальной динамики, в статистическом исследовании проводятся предварительные расчеты (смыкание рядов динамики), которые предшествуют статистическому анализу динамических рядов. Под Ряды динамики: Смыканиесмыканием рядов динамики понимается объединение в один ряд двух и более рядов, уровни которых рассчитаны по разной методологии или не соответствуют территориальным границам и т.д. Смыкание рядов динамики может предполагать также приведение абсолютных уровней рядов динамики к общему основанию, что нивелирует несопоставимость уровней рядов динамики.

Абсолютный прирост выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения.

Абсолютный прирост (базисный)  (9.1)

где y_i - уровень сравниваемого периода; y₀ - уровень базисного периода.

Абсолютный прирост с переменной базой (цепной), который называют скоростью роста,  (9.2)

где y_i - уровень сравниваемого периода; y_i-1 - уровень предшествующего периода.

Коэффициент роста K_i определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста.

Коэффициент роста базисный  (9.3)

Коэффициент роста цепной  (9.4)

Средний темп роста, %. Это средний коэффициент роста, который выражается в процентах:  (9.16)

Средний темп прироста  , %. Для расчета данного показателя первоначально определяется средний темп роста, который затем уменьшается на 100%. Его также можно определить, если уменьшить средний коэффициент роста на единицу:  (9.17)

Среднее абсолютное значение 1% прироста можно рассчитать по формуле
15.важнейшие показатели анализа динамических рядов

Абсолютное ускорение — разница между абсолютным приростом за данный период и абсолютным приростом за предыдущий период равной длительности. Измеряется только цепным способом

Относительное ускорение — отношение цепного темпа прироста за данный период и цепного темпа прироста за предыдущий период

Абсолютное значение одного процента прироста A_i . Этот показатель служит косвенной мерой базисного уровня. Представляет собой одну сотую часть базисного уровня, но одновременно представляет собой и отношение абсолютного прироста к соответствующему темпу роста.

Данный показатель рассчитывают по формуле

Абсолютный прирост выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения.

Абсолютный прирост (базисный)  (9.1)

где y_i - уровень сравниваемого периода; y₀ - уровень базисного периода.

Абсолютный прирост с переменной базой (цепной), который называют скоростью роста,  (9.2)

где y_i - уровень сравниваемого периода; y_i-1 - уровень предшествующего периода.

Коэффициент роста K_i определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста.

Коэффициент роста базисный  (9.3)

Коэффициент роста цепной  (9.4)

Темп роста  (9.5)

Темп прироста Т_П определяется как отношение абсолютного прироста данного уровня к предыдущему или базисному.

Темп прироста базисный  (9.6)

Темп прироста цепной  (9.7)

Темп прироста можно рассчитать и иным путем: как разность между темпом роста и 100 % или как разность между коэффициентом роста и 1 (единицей): 1) Т_п = Т_р - 100%; 2) Т_п = K_i - 1. 
16.статистические индексы, их виды, построение и особенности

Динамика одноименных явлений изучается с помощью индивидуальных индексов:

- индивидуальный индекс физического объема продукции,

- индивидуальный индекс цен,

- индивидуальный индекс товарооборота, где подстрочное обозначение «0» соответствует уровню базисного периода (с которым сравнивают) или момента времени, «1» - уровню отчетного (сравниваемого) периода или момента времени.

Основной формой сводных (общих) индексов являются агрегатные индексы. 1)  - агрегатный индекс товарооборота, гдеpq – индексируемое сложное явление.

Разница между числителем и знаменателем индекса составляет абсолютное изменение товарооборота:  .

Это изменение товарооборота является результатом действия двух факторов: изменения физического объема продукции и изменения уровня цен.

Влияние изменения количества выпущенной продукции на изменение общего товарооборота отражается агрегатным индексом физического объема  . Влияние изменения цен выражается агрегатным индексом цен  .

2)  - агрегатный индекс физического объема продукции, где - индексируемая величина, - соизмеритель, или вес, который фиксируется на уровне одного и того же периода. Разница между числителем и знаменателем индекса означает абсолютное изменение товарооборота (прирост или снижение) за счет изменения физического объема продукции:

.

3)  - агрегатный индекс цен, где  – индексируемая величина,  – соизмеритель, или вес, который фиксируется на уровне одного и того же периода (в данном случае – на уровне отчетного периода).

Разница между числителем и знаменателем индекса означает абсолютное изменение товарооборота (прирост или снижение) за счет изменения цен, или экономию (перерасход) потребителя за счет изменения цен:  .

Между рассмотренными сводными индексами в агрегатной форме существует взаимосвязь:  , кроме того, .

Индекс переменного состава I_пер представляет собой отношение двух взвешенных средних величин, характеризующее изменение индексируемого (усредняемого) показателя.

Величина этого индекса характеризует изменение средней взвешенной за счет влияния двух факторов: усредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.

Индекс постоянного (фиксированного) состава I_фикс представляет собой отношение средних взвешенных с одними и теми же весами (т.е. при постоянной структуре).

Индекс постоянного состава учитывает изменение только индексируемой величины и показывает средний размер изменения изучаемого показателя у единиц совокупности.

Индекс структурных сдвигов I_стр характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя.

Система взаимосвязанных индексов при анализе динамики средних величин имеет вид:  .
17.общие индексы и правила их построения

Индексируемой величиной называется показатель (признак), изменение которого выявляют. Весом называется показатель, который выступает в качестве соизмерителя.

Существует правило построения агрегатных факторных индексов, в соответствии с которым в индексах качественных показателей весами выступают показатели отчетного периода, а в индексах количественных показателей – базисного периода.

Так, агрегатный индекс цен (J_p) определяется по формуле



где р₀, р₁ – цена каждого вида продукции (товара) соответственно в базисном и отчетном периодах (индексируемый показатель);

q₁ – объем каждого вида продукции (товара) в отчетном периоде (вес индекса).

Этот индекс характеризует, как изменились в среднем цены на различные виды продукции (товаров), включенные в расчет общего индекса цен.

Агрегатный индекс физического объема (J_q) рассчитывается по следующей формуле:



где q₀ – объем каждого вида продукции (товара) в базисном периоде.

Индекс физического объема характеризует, как изменился в среднем общий объем продукции по анализируемому перечню.

Индекс стоимости продукции товарооборота (J_рq) определяется следующим образом:



Данный индекс характеризует изменение фактической стоимости произведенной или реализованной продукции или же размера товарооборота по анализируемому перечню.

Произведение агрегатного индекса цен на агрегатный индекс физического объема равно агрегатному индексу стоимости продукции (товарооборота):

J_p  J_q = J_pq.

Используя эту взаимосвязь, можно по двум известным индексам определить третий. Общие индексы дают возможность определить не только относительные изменения явления, но и найти абсолютные значения изменений как разницу между числителем и знаменателем соответствующих индексов.

Абсолютное изменение общей стоимости продукции (товаров) исчисляется по формуле



в том числе за счет следующих факторов:

 изменения уровней цен:  ;

 изменения физического объема продукции (товаров):



где p₀q₀ и p₁q₁ – стоимость произведенной или реализованной продукции (товарооборота) соответственно в базисном и отчетном периодах;

p₀q₁ – стоимость продукции (товарооборот) в сопоставимых ценах.

При этом должно соблюдаться следующее равенство:

pq = pq(p) +pq(q).

Аналогично агрегатным индексам цен физического объема и стоимости продукции (товарооборота) строятся и рассчитываются агрегатные индексы других взаимосвязанных экономических показателей.

18.порядок приведения данных к сопоставимому виду при составлении общих индексов (весы, индексируемая величина и ее виды)

Приведение статистических данных к сопоставимому виду представляет собой устранение причин несопоставимости статистических данных в пространстве, во времени, в содержании или методологии их расчета. Оно достигается пересчетом данных: приведением данных к одним и тем же единицам измерения; отграничением и выделением из всего объема данных однородной и сопоставимой совокупности (сопоставимого круга); заменой абсолютных величин относительными величинами; заменой абсолютных величин средними величинами; специальной группировкой материала; перегруппировкой данных (метод вторичной группировки); стандартизацией структуры совокупности; классификацией статистических данных. Если сопоставляются данные в денежном выражении и оказывается, что они несопоставимы вследствие того, что в одних случаях был принят один уровень цен, в других – другой, то данные могут быть приведены к сопоставимому виду пересчетом в единые, так называемые сопоставимые, или неизменные цены. Это может быть достигнуто прямой непосредственной оценкой изучаемого показателя или отдельных его элементов в сопоставимых ценах или посредством индекса цен.

Многие показатели измеряются в разных единицах измерения, что затрудняет сопоставление данных, приведение таких данных к одним и тем же единицам измерения во многих случаях производится при помощи соответствующих коэффициентов перевода одних единиц измерения в другие (использование, например, условно–натуральных единиц).

1. Периодизация развития, т. е. расчленение его во времени на однородные этапы, в пределах которых показатель подчиняется одному закону развития. Это, по существу, типологическая группировка во времени. Периодизация может осуществляться несколькими методами:

- исторический метод. Периодизация осуществляется на основе узаконенной структуры динамики. При этом обращают внимание на значимые даты и события, а именно: время принятия управленческих решений по данному показателю, смену хозяйственного механизма, смену руководства, войны и т. п. Недостатком этого механизма является то, что точные временные границы периодов путем теоретического анализа удается получить крайне редко;

- метод параллельной периодизации. Идея этого метода заключается в следующем. Пусть У - анализируемый показатель, развернутый в динамический ряд (У), где Yt - значение уровня ряда в момент (интервал) времени t. Возможно, существует показатель X которому соответствует динамический ряд (X), определяющий поведение исследуемого показателя У. Тогда в роли однокачественных периодов Y нужно взять периоды X.

- методы многомерного статистического анализа. Часто требуется выделить однокачественные периоды в развитии явлений или процессов, получить адекватное отображение которых с помощью одного лишь показателя труда. К таковым относятся, в частности, здоровье населения, развитие сельскохозяйственного производства и др.

2. Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчетов.

3. Величины временных интервалов должны соответствовать интенсивности изучаемых процессов. Чем больше вариация уровней во времени, тем чаще следует делать замеры. Соответственно, для стабильных процессов интервалы можно увеличить.

4. Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней , если же такие пропуски неизбежны, то их восполняют условными расчетными значениями

19.взаимосвязь количественных и качественных показателей

Количественный и качественный анализ — взаимодополняющие методы, которые можно объединить в опросах, чтобы получить всеобъемлющие результаты.

Проще говоря, количественные данные дают Вам числа для подтверждения общих пунктов Вашего исследования. Качественные данные обеспечивают подробности для глубокого понимания их полных последствий.

Количественные данные представляют собой голые факты — цифры. Количественные данные структурированы и статистически обработаны. Они помогают сделать общие выводы из исследования.