электричество 2 часть. 12 вопрос. Поведение вещества в электрическом поле
 Скачать 0.68 Mb.
|
|
12 вопрос. Поведение вещества в электрическом поле. По электрическим свойствам все вещества можно разделить на: - проводники - диэлектрики - полупроводники (промежуточное значение) - электреты, сегнетоэлектрики, пьезоэлектрики (уникальные свойства) Проводники – это вещества проводящие электрический ток. Различают: I рода: металлы; II рода: растворы электролитов, газы при определенных условиях (ионизированные газы). Поведение вещества в электрическом поле определяется структурой вещества. Вещество состоит из атомов – нейтральных электрических систем, т.е. положительно заряженного ядра и электронов вращающихся вокруг него. У проводников электроны внешних валентных слоев слабо связаны с ядром, что позволяет свободно им свободно перемещаться по объему проводника. В металлах есть носители тока: свободные электроны. В диэлектриках (смолы, пластмассы, дерево, стекло) электроны внешних валентных оболочек привязаны к ядру и свободно перемещаться не могут. Они находятся в связанном состоянии. У диэлектрика нет носителей тока!!!! Он не проводит электрический ток!!!!! У полупроводников свободные носители заряда появляются при определенных внешних условиях: повышение температуры, повышение давления. Вопрос 13. Проводники в электрическом поле. Метод изображений. Возьмем проводник и поместим его в электростатическое поле. 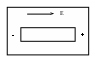 По принципу суперпозиции результирующее поле внутри проводника:  Б 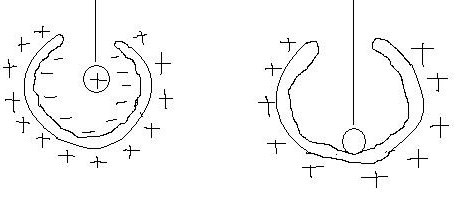 удем наблюдать явление электростатической индукции (пример закона сохранения заряда) – явления разделения электрических зарядов внутри проводника, помещенного во внешнее электростатическое поле, приводящее к появлению на поверхности проводника поверхностных зарядов, а внутри проводника результирующее поле будет равно 0, происходящее за время релаксации  .По закону макроскопической необратимости любая неравновесная система переходит в состояние равновесия, в котором может находиться сколь угодно долго, до тех пор пока внешнее воздействие не выведет ее из состояния равновесия. Время перехода в состояние равновесия – время релаксации. Свойства: 1. Внутри проводника помещенного во внешнее электростатическое поле  (внутри проводника поле равно 0) Силовые линии должны быть перпендикулярны поверхности проводника (нет движения зарядов ни внутри ни на поверхности проводника). На поверхности есть заряд (эл. поле), значит  (касательное направление поля), следовательно сила вдоль поверхности  !!! Нет движения зарядов по поверхности!!! 2. Силовые линии эл. поля перпендикулярны поверхности проводника  3. Поверхность проводника эквипотенциальна ( все точки поверхности имеют одинаковый потенциал), следовательно внутри проводника нет объемных зарядов, следовательно весь объем проводника эквипотенциален. 4. поле внутри полости. Пусть в заряженном проводнике (помещенном в эл. поле) есть полость. Найдем поле внутри этой полости. Предположим, что поле 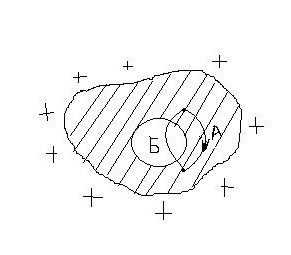 внутри полости равно 0.   (теорема о циркуляции) Поле внутри полости заряженного проводника равно нулю!!! 5. Заряды на поверхности располагаются так, чтобы их взаимная потенциальная энергия была минимальна (где радиус кривизны минимален). 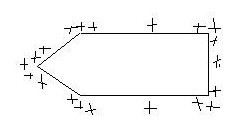 - поверхностная плотность индуцированных зарядов (заряд приходящийся на единицу площади).  - радиус кривизны. Где радиус кривизны меньше, там  больше (острие проводника). Данное явление называется стекание зарядов с острия проводника. В/м (в области острей). Сильное эл. поле (около острей) ионизирует среду и может привести к пробою диэлектрика, к возникновению коронного разряда. Явление электромагнитной индукции наблюдается в опытах Фарадея (один из опытов – это опыт иллюстрирующий принцип действия зарядного устройства, так называемая балка Фарадея). Повторяя процедуру можно добиться большего заряда на поверхности. Перечисленные свойства справедливы для: незаряженного проводника в электростатическом поле; для заряженного проводника. Метод изображения – используется, если есть проводящие поверхности и точечные заряды. П 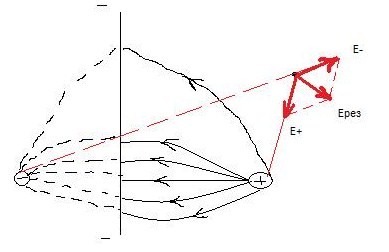 оле образованное точечными зарядами и проводящими поверхностями есть суперпозиция точечных зарядов и их изображений.Вопрос 14. Диэлектрики в электрическом поле. Поляризация диэлектриков. Полярные и неполярные диэлектрики. Сегнетоэлектрики, пьезоэлектрики, пироэлектрики, электреты. Прямой и обратный пьезоэлектрические эффекты и их применение. При помещении диэлектрика в электрическое поле происходит поляризация диэлектрика, приобретение объемом диэлектрика объемного связанного заряда. Поле внутри диэлектрика есть и оно ослабляет внешнее электрическое поле. Заряды внутри диэлектрика называют связанными зарядами, а заряды которые помещаются в диэлектрик из вне и заряды сторонних тел – свободными (сторонними) зарядами. Поведение диэлектриков определяется их внутренним строением. В молекуле диэлектрика нет свободных валентных электронов; заряды привязаны к ядру. Введем понятие центра положительного и отрицательного зарядов: 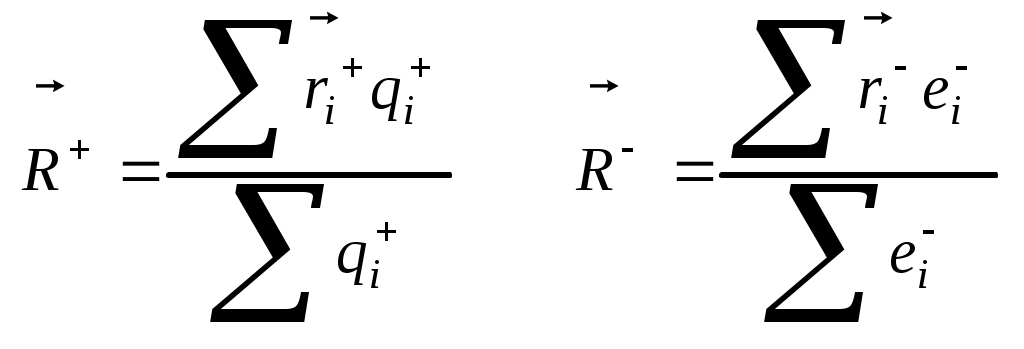 I. Неполярные диэлектрики – молекулы у которых совпадают  (например: молекулы атома Н2, О2); молекулы симметричны; Не обладают изначальным дипольным моментом р=0II. Полярные диэлектрики – молекулы, у которых центры положительных и отрицательных зарядов не совпадают:  . В молекулах (например Н2О) пространственно разделены центры положительных и отрицательных зарядов; Дипольный момент не равен нулю, даже в отсутствии внешнего поля:  . Сегнетоэлектрики, пьезоэлектрики, пироэлектрики, электреты. Сегнетоэлектрики, пьезоэлектрики, пироэлектрики и электреты относят к нелинейным диэлектрикам. Нелинейные диэлектрики – вещества, у которых модуль вектора поляризации не линейно зависит от величины внешнего электрического поля. I. Электреты (смолы, стекла, воск). диэлектрики, способные длительное время находиться в наэлектризованном состоянии после снятия внешнего воздействия, вызвавшего электризацию (электрические аналоги постоянных магнитов). Получают из восков и смол, полимеров, неорганических диэлектриков, охлаждая их в сильном электрическом поле (термоэлектреты) или облучая светом фотопроводящие диэлектрики в сильном электрическом поле (фотоэлектреты). Применяются в качестве источников постоянного электрического поля в технике связи (микрофоны и телефоны), как чувствительные датчики в дозиметрии, как пьезодатчики и т. д. II. Пьезоэлектрики – кристаллы. Поляризуются при механическом воздействии (сжатие, растяжении). Каждый пьезоэлектрик является электромеханическим преобразователем. Если его поместить в переменное электрическое поле, то амплитуда механических колебаний удет меняться с частотой переменного поля. III. Сегнетоэлектрик. Сильно поляризуются под действием внешнего электрического поля. Эти нелинейные свойства сохраняются в некотором температурном интервале. Для них характерна некоторая температура – точка Кюри – выше этой точки сегнетоэлектрики теряют свою нелинейность. Домен – макроскопическая область, ниже температуры Кюри, в которой дипольные моменты атомов имеют строгую ориентацию. Если сегнетоэлектрик поместить в поле, то домены будут перестраиваться по направлению внешнего электрического поля. Нелинейные свойства определяют домены. Сегнетоэлектрики являются очень хорошими диэлектриками. К сегнетоэлектрикам относятся сегнетова соль, титанат бария (BaTiO3), дигидрофосфаты калия (KH2PO4) и аммония, ниобат лития (LiNbO3) и др. Известно несколько сотен сегнетоэлектриков, в т. ч. сегнетокерамика. Применяются главным образом как пьезоэлектрические преобразователи в детекторах электромагнитных излучений, а также в различных конденсаторах. IV. Пироэлектрики. кристаллические диэлектрики, на поверхности которых при изменении температуры появляются электрические заряды. Пироэлектриками могут быть лишь нецентросимметричные кристаллы. Все пироэлектрики являются пьезоэлектриками (но не обратно), некоторые пироэлектрики обладают сегнетоэлектрическими свойствами. Типичный пироэлектрик — турмалин. Прямой и обратный пьезоэлектричекий эффекты и их применение В  озникновение электрической поляризации в веществе в отсутствие электрического поля при упругих деформациях (прямой пьезоэлектрический эффект) и появление механических деформаций под действием электрического поля (обратный пьезоэлектрический эффект). Первое исследование пьезоэлектрического эффекта осуществлено П. Кюри (1880) на кристалле кварца. Пьезоэлектрический эффект обнаружен более чем у 1500 веществ. Пьезоэлектрический эффект наблюдается у всех сегнетоэлектриков и у многих пироэлектриков. Прямой пьезоэффект используют в технике для преобразования механических напряжений или деформаций в электрические сигналы (звукосниматели, датчики деформаций, приемники ультразвука и др.) Обратный пьезоэффект используется для преобразования электрических сигналов в механические (акустические излучатели, генераторы ультразвука и др.)Вопрос 15. Свободные и связанные заряды. Вектор поляризации (поляризованность). Поверхностная плотность связанных зарядов. Связь вектора поляризации с поверхностной плотностью связанных зарядов. 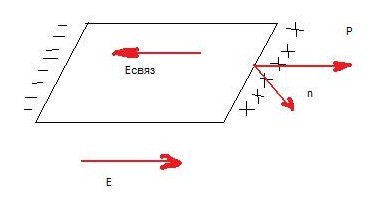 Связанные заряды внутри компенсируют друг друга. Некомпенсированный заряд находится на внешних поверхностях диэлектрика.  Поверхностная плотность связанных зарядов - физическая величина показывающая степень поляризации диэлектрика и равная заряду приходящемуся на единицу площади.  Вектор поляризации – векторная физическая величина характеризующая степень поляризации диэлектрика и равная дипольному моменту в единице объема.  Связь вектора поляризации с поверхностной плотностью связанных зарядов. Рассмотрим поведение диэлектрика во внешнем электрическом поле в виде косого параллепипеда; углы 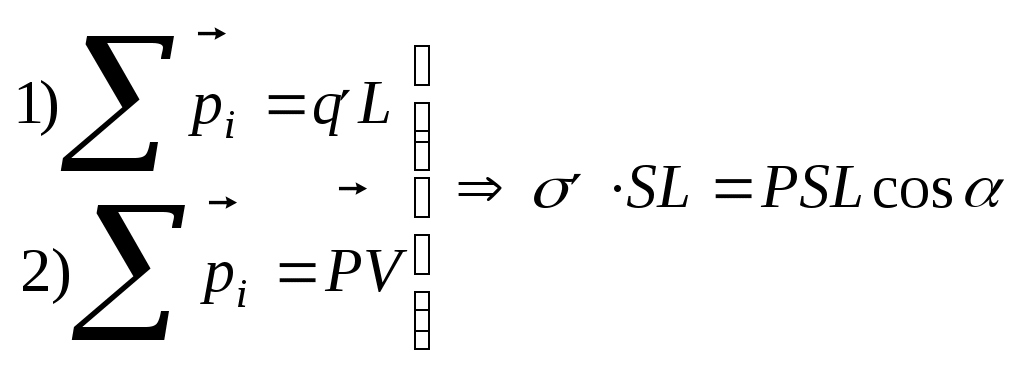 образуют торцы с внешним электрическим полем. Всему объему можно приписать: 1)Полный дипольный момент всего .образца – есть заряды на расстояние между ними.  Получили что, поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации диэлектрика. Поляризация диэлектрика пропорциональна величине внешнего поля  Вопрос 16. Неполярные диэлектрики. Электронная поляризация.  Механизм электронной поляризации: Смещение электронных облаков орбит под действием электрического поля. Степень поляризации не высока, зависит от внешнего электрического поля. Электронная поляризация не зависит от температуры. Вопрос 17. Полярные диэлектрики. Ориентационная поляризация Атомы и молекулы полярных диэлектриков изначально обладают дипольным моментом. Если внешнее поле отсутствует то дипольные моменты отдельных молекул ориентированы в пространстве хаотично. I.  II.  Д  иполь совершает колебательные движения, колебания затухают, диполь встает носом по полю, т.к. это положение устойчивого равновесия. Механизм ориентационной поляризации – поворот диполей под действием внешнего электрического поля. Имеет место влияние температуры. 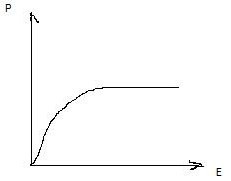 Степень поляризации значительна!!!!! Поляризация обратнопропорциональна температуре  Вопрос 18. Поток вектора напряженности электрического поля сквозь поверхность. Теорема Гаусса (интегральная и дифференциальная формулировки). Поток в электродинамике аналогичен потоку жидкости и газа в гидродинамике. 1. Линии  перпендикулярны площадке   Поток через площадку равен:  Так как количество линий  , пронизывающих единицу площади поверхности, перпендикулярной к ним, численно равно Е (модулю вектора ), то число пересечений этих линий с площадкой равно:  2. Линии пересекают плоскую площадку под произвольным углом к нормали  .  Поток вектора через площадку равен:  Следовательно, поток  через площадку , произвольно расположенную в электрическом поле, численно равен количеству пересечений  линий с этой площадкой. Для того, чтобы знак совпадал со знаком , нужно считать положительными те пересечения, для которых угол меду векторами и является острым. Пересечения, для которых угол является тупым, нужно считать отрицательными. Для однородного электрического поля и плоской поверхности применима одна из этих формул:  Поток через произвольную поверхность: В случае замкнутой поверхности положительной принято считать нормаль направленную наружу области, охватываемой этой поверхностью. Следовательно, в случае выхода линии наружу из области, ограниченной замкнутой поверхностью, угол между векторами и является острым и такое пересечение считается положительным, а в случае входа линии внутрь этой области угол является тупым и такое пересечение считается отрицательным.Теорема Гаусса 1. Интегральная форма  Поток вектора Е сквозь замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на  .2. Дифференциальная форма  Дивергенция поля Е в данной точке зависит только от плотности электрического заряда  в той же точке и больше ни от чего. Вопрос 19. Теорема Гаусса для электрического поля в вакууме и в веществе. Вектор электростатического смещения (вектор электростатической индукции). Диэлектрическая восприимчивость и диэлектрическая проницаемость вещества. Смысл  . Закон Кулона для взаимодействия зарядов в веществе.  Теорема гаусса для электрического поля в вакууме  Рассмотрим точечный заряд в диэлектрике. Диполи диэлектрика поворачиваются «носом» по полю. Поверхность S в виде сферы «разрезает» диполи; На поверхности оказывается положительный связанный заряд, а внутри поверхности отрицательный связанный заряд.  Заряды создающие поле которые вносят в диэлектрик снаружи, есть свободные или сторонние заряды.   вектор поляризации.  Под знаком интеграла стоит сумма двух векторов. Вектора поля сторонних зарядов и вектора поля связанных зарядов. - вектор электростатического смещения (электростатической индукции).  Вектор формальный; физического смысла не имеет.  Эта формула выражает теорему Гаусса для вектора : поток вектора электрического смещения через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных зарядов. Вектор поляризации зависит от внешнего поля:   - диэлектрическая восприимчивость (всегда положительна). Диэлектрическая проницаемость - физическая величина, характеризующая способность диэлектрика поляризоваться в электрическом поле. Всегда больше единицы. Для вакуума  =1, так как Р=0,  Для однородного диэлектрика:  Физический смысл Рассмотрим точечный заряд в вакууме и диэлектрике.    Силовые линии одинаковы в вакууме и диэлектрике. На границе раздела сред не рвутся. Могут начинаться и заканчиваться только на свободных зарядах. Диэлектрическая проницаемость показывает во сколько раз поле в вакууме больше чем в диэлектрике. Вопрос 20. Поле на границе раздела двух диэлектрических сред. Граничные условия для напряженности и вектора электростатической индукции электрического поля. Путь электрическое поле переходит из одного однородного диэлектрика в другой, который отличается только диэлектрической проницаемостью. 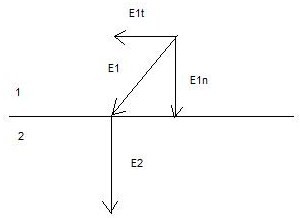 Разложим вектор Е1 на две составляющие: 1)  - перпендикулярную границе раздела диэлектрика.2)  - параллельную границе раздела диэлектрика.Для того чтобы установить законы, согласно которым изменяются 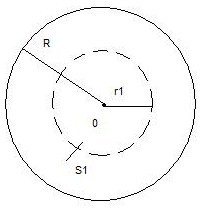и при переходе воспользуемся теоремой о циркуляции вектора напряженности электрического поля и теоремой Гаусса.   Выберем контур который охватывает малую часть границы раздела. Стороны контура, параллельные границе раздела, имеют такую длину, что поле Е в ее пределах в каждом диэлектрике можно считать одинаковым, а высота контура пренебрежимо мала. Согласно теореме о циркуляции вектора Е:  (1)При переходе электрического поля из одного диэлектрика в другой тангенциальная оказывается одинаковой по обе стороны границы раздела (не претерпевает скачка). Условия для вектора . Возьмем очень малой высоты цилиндр, расположив его на границе раздела двух диэлектриков. Сечение цилиндра должно быть таким, чтобы в пределах каждого его торца вектор D был одинаков. Тогда согласно теореме Гаусса для вектора D:  где - поверхностная плотность стороннего заряда на границе раздела.  . Из этого соотношения видно, что нормальная составляющая вектора D претерпевает скачек при переходе границы раздела. Но если сторонние заряды на границе раздела отсутствуют ( ), то в этом случае нормальные составляющие вектора D скачка не испытывают, они оказываются одинаковыми по разные стороны границы раздела  (2). Таким образом, если на границе раздела двух однородных изотропных диэлектриков сторонних зарядов нет, то при переходе этой границы составляющие  и  изменяются непрерывно, без скачка. Составляющие же  и  претерпевают скачек. Преломление линий Е и D. Найдем соотношение между углами  и  . Если сторонних зарядов на границе раздела нет, то согласно (1) и (2)  Из рисунка следует, что  Отсюда с учетом предыдущих условий получаем закон преломления Е, а значит и D:  Это означает, что в диэлектрике с большим значением линии Е и D будут составлять больший угол с нормалью к границе раздела.Вопрос 21. Применение теоремы Гаусса для расчета электрических полей. Электрическое поле: 1) бесконечной равномерно заряженной плоскости; 2) вблизи заряженной металлической поверхности; 3) заряженного проводящего шара; 4) бесконечно равномерно заряженной нити; 5) однородно заряженного диэлектрического шара; 6) бесконечной равномерно заряженной по объему диэлектрической пластины конечной толщины. 1) Поле бесконечной равномерно заряженной плоскости. Пусть поверхностная плотность заряда  . Благодаря равномерному распределению заряда по бесконечной плоскости, поле, созданное им, обладает плоской симметрией. Это означает, что линии электрического смещения направлены перпендикулярно плоскости. Кроме того, в симметричных относительно плоскости точках векторы одинаковы по модулю, но противоположны по направлению. Поток сквозь боковую поверхность цилиндра равен нулю, поэтому полный поток через всю поверхность цилиндра будет равен:  , где - площадь каждого торца. Внутри цилиндра заключен заряд  . Согласно теореме Гаусса  откуда получаем выражение:  , т.к.  то  3) Поле заряженного проводящего шара. Пусть заряд равномерно распределен по шару радиуса R. Поле такой системы центрально симметричное, поэтому для нахождения поля следует в качестве замкнутой поверхности взять концентрическую сферу. 1)  По теореме Гаусса:  Для точек сферы S1:     2) 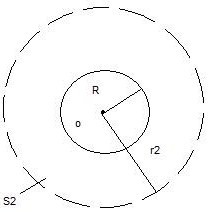  Для точек сферы S2:    Формулы можно преобразовать с помощью:  4) Поле бесконечной равномерно заряженной нити. 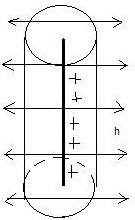 Нить тонкая и равномерно заряженная. Заряд неподвижен. Поле обладает цилиндрической симметрией. На расстоянии R модуль напряженности электрического поля постоянен. Учитывая симметрию распределения заряда, в качестве гауссовской поверхности выберем цилиндр, геометрический центр которого совпадает с нитью. Длина образующей H. Радиус основания цилиндра R.  - линейная плотность заряда. Согласно теореме Гаусса: . Полный поток вектора Е через цилиндр будет равен потоку через его боковую поверхность:   5) Поле однородно заряженного диэлектрического шара. Расчет аналогичен полю заряженного проводящего шара. Для нахождения поля внутри шара нужно применить теорему Гаусса в виде 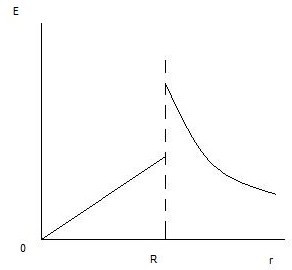 . И за принять   График зависимости Е от r поля равномерно заряженного диэлектрического шара. В рассмотренном случае диэлектрическая проницаемость вещества принята равной  поэтому при перехода через поверхность шара напряженность скачкообразно меняется в 2 раза. Вопрос 22. Электрическая емкость уединенного проводника. Емкость уединенного заряженного проводящего шара. Рассмотрим процесс зарядки удаленного от других тел проводника. Сообщим ему заряд q. В результате этого заряд проводника станет равным  . Этот заряд распределится по поверхности проводника так, чтобы напряженность поля внутри проводника стала равной нулю, а его поверхность стала эквипотенциальной. Пусть значение потенциала этой поверхности равно  . Если теперь вновь сообщить проводнику такой же заряд q, то предыдущий заряд на проводнике не будет влиять на распределение нового заряда, так как внутри проводника напряженность поля  . Следовательно новый заряд q распределится по поверхности точно так же, как и первый. В этом случае и заряд и потенциал проводника увеличится вдвое. При сообщении проводнику заряда q в n-ый раз все повторится:  . Таким образом потенциал  уединенного проводника будет все время пропорционален находящемуся на нем заряду  .  где С – коэффициент пропорциональности называемый электроемкостью уединенного проводника. Физический смысл:  (1). Электроемкость уединенного проводника численно равна заряду, который нужно сообщить этому незаряженному проводнику чтобы его потенциал стал равным единице  . Единица емкости – фарад (Ф).  Емкость уединенного проводящего шара. Радиус шара R. Шар находится в однородном и изотропном безграничном диэлектрике с проницаемостью . Сообщим шару заряд q и вычислим его потенциал  (2).Из (1) и (2) следует формула емкости уединенного проводящего шара:  Из этого выражения следует что электроемкость уединенного проводящего шара определяетя его размерами (R) и диэлектрическими свойствами среды, в которой он находится. В общем случае электроемкость уединенного проводника зависит также от его формы. |