18620 Механика грунтов. 12. Закон Кулона для песчаных и глинистых грунтов. 9
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
29.Условия предельного равновесия.Предельным равновесием основания называют такое напряженное состояние, при котором незначительное увеличение внешней нагрузки приведет к нарушению установившегося равновесия и вызовет потерю устойчивости грунта, сопровождающееся выпором грунта из-под подошвы сооружения со значительным нарастанием осадки. В зависимости от величины внешней нагрузки на грунт различают два понятия: допредельное и предельное. Первое характеризуется вполне определенными деформациями, изменение которых может произойти из-за повышения уровня напряжений или в результате временных эффектов (консолидации, ползучести). Приближенно можно полагать, что в диапазоне допредельных напряженных состояний, относительно «далеких» от предельного, справедлива линейная связь между напряжениями, подобная закону Гука. Отсюда следует возможность использования в механике грунтов решений теории упругости. Второе состояние характеризуется достижением напряжениями такой критической комбинации, при которой устанавливается предельное равновесие между внешней нагрузкой и внутренними силами сопротивления грунта. Наступление предельного равновесия основания может быть вызвано различной комбинацией напряжений, в зависимости от которой различают условия предельного состояния, или, как их иногда называют, теории прочности. Для изучения прочности грунта в условиях сложного напряженного состояния применяют два основных условия (теории): условие , согласно которому предельное состояние наступает при отдельном соотношении касательного и нормального напряжений, действующих на одной площадке; условие Мизеса — Шлейхера, согласно которому предельное состояние наступает при определенном соотношении интенсивности касательных напряжений и среднего нормального напряжения. Остановимся на теории Кулона — Мора. Пусть к граням элементарного объема грунта приложены главные напряжения σ1≥σ2≥σ3 (рис. 8.1,а). 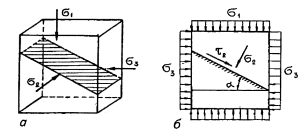 Рис. 8.1. Положение площадки скольжения (а) и напряжения на наклонной площадке (б) Увеличивая постепенно главное напряжение σ1 и оставляя постоянной величину 0-3, в соответствии с теорией Кулона — Мора произойдет сдвиг по некоторой площадке, наклоненной к горизонтальной плоскости, причем промежуточное главное напряжение σ2 будет действовать параллельно этой площадке. В отличие от схемы одноплоскостного сдвига в случае сложного напряженного состояния положение этой площадки неизвестно. В теории Кулона — Мора принимается, что на площадке скольжения выполняется условие для несвязных или для связных грунтов. Для того чтобы определить положение площадки скольжения, воспользуемся известными из сопротивления материалов выражениями для касательного и нормального напряжений на наклонной площадке (рис. 8.1,6). Согласно уравнения, на площадке скольжения эти напряжения в предельном состоянии будут связаны выражением Для представления напряженного состояния грунта используют графические изображения, известные под названием кругов Мора. Они дают возможность исследовать напряжения на площадке с любым наклоном, проходящим через рассматриваемую точку. Построение круга Мора Круг Мора (рис. 8.2) вычерчивается в прямоугольной системе координат. Полагается, что σ1≥σ2 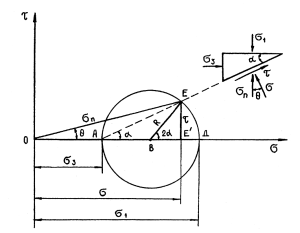 Рис. 8.2. Графическое представление напряженного состояния грунта (круг Мора) 30.Первая (начальная) критическая нагрузка.Критическая нагрузка это нагрузка, соответствующая началу возникновения в грунте зон сдвигов и окончанию фазы уплотнения, когда под краем нагрузки возникают между касательными и нормальными напряжениями соотношения, приводящие грунт (сначала у ребер подошвы фундамента) в предельное напряженное состояние. Эту нагрузку называют начальной критической нагрузкой. Она совершенно безопасна в основаниях сооружений, так как до ее достижения грунт всегда будет находиться в фазе уплотнения. Начальная критическая нагрузка характеризует пределы применимости теории линейно-деформируемой среды. Начальная критическая нагрузка характеризует пределы применимости теории линейно-деформируемой среды. Если давление на грунт не превышает эту нагрузку, то ни в одной точке грунтового массива касательное напряжение не превосходит предельное. При превышении же этой нагрузки в грунте происходит формирование зон предельного состояния. Начальным критическим давлением на основание называется то значение давления, при котором в грунте основания возникают области предельного напряженного состояния. При давлениях меньших начальных критических значений во всех точках основания (рис. 6.5) напряженные состояния допредельные, что совершенно безопасно для оснований сооружений. В этом случае до достижения начального критического давления грунт находится в фазе уплотнения (см. рис. 6.6) и подход к ее определению демонстрируется для полосовой нагрузки на грунт. На рис. 8.5 представлены ее реальная и расчетные схемы. 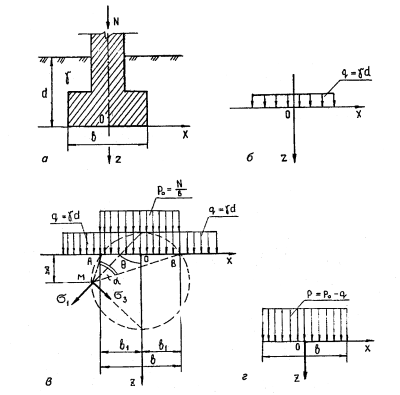 Рис. 8.5. Реальная (а) и расчетные (б, в, г) схемы к определению начального критического давления Для нахождения начального критического давления значения главных напряжений σ1 и σ3 определяются с учетом приложенной нагрузки Р = Р0— q и соответственно веса грунта. Вертикальное сжимающее напряжение (давление) от собственного веса грунта в точке М (см. рис. 8.5,в), лежащей на глубине z от подошвы фундамента, определяется из выражения Полные главные напряжения в грунте на глубине : На площадках сдвига, когда грунт от действия нагрузки находится в конце среза уплотнения, имеет место предельное равновесие: Тогда, подставив (8.19) и (8.20) в (8.21), получим уравнение кривой, соответствующей границе пластической зоны грунта: Выражение (8.22) можно рассматривать как уравнение границы области, проходящей через точку М (см. рис. 8.5,в), на контуре которой при действии под подошвой фундамента давления Р имеет место состояние предельного равновесия. Координаты точек этой границы определяются неизвестными z и α. Решая уравнение (8.22) относительно z, получим: Приравняв первую производную этого выражения по α нулю, находим максимальную глубину границы этой области zmax, где площадка скольжения получает опасный наклон к горизонту: 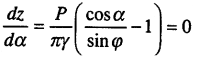 (8.24) (8.24)Из уравнения (8.24) следует, что при z = zmax, cosα = sinφ или α = π/2-φ Тогда, подставляя (8.25) в формулу (8.24), получаем выражение для низкой точки сдвига грунта (zmax) в следующем виде: Решая это относительно Р = Рсr найдем такое значение критического давления, при котором область предельного равновесия развивается на заданную глубину zmах: (8.27) Исходя из условия, что начальное критическое давление соответствует отсутствию пластических деформаций во всех точках основания, т.е. zmax = 0, имеем формула (8.28) Это и есть формула для определения начального критического давления на грунт основания. Формула (8.28) (при с = 0) была получена Н.П. Пузыревским (1923) и, как правило, называется его именем. Практика показывает, что фундамент, спроектированный таким образом, что давление под его подошвой не превышало бы начального критического давления, будет иметь экономически невыгодные размеры. |
