18620 Механика грунтов. 12. Закон Кулона для песчаных и глинистых грунтов. 9

• Название: 12. Закон Кулона для песчаных и глинистых грунтов. 9
• Анкор: 18620 Механика грунтов.docx
• Дата: 28.01.2017
• Размер: 1.05 Mb.
• Имя файла: 18620 Механика грунтов.docx
• Тип: Закон; #755
• страница: 9 из 20

18.Определение напряжений от нагрузки, распределенной по ограниченному контуру.

Действие равномерно распределенной нагрузки

В 1935 г. А. Лявом были получены значения вертикальных сжимающих напряжений в любой точке основания от действия нагрузки интенсивностью , равномерно распределенной по площади прямоугольника размером .

Практический интерес представляют компоненты напряжений , относящиеся к вертикали, проведенной через угловую точку этого прямоугольника, и , действующие по вертикали, проходящей через его центр (рис. 3.8.).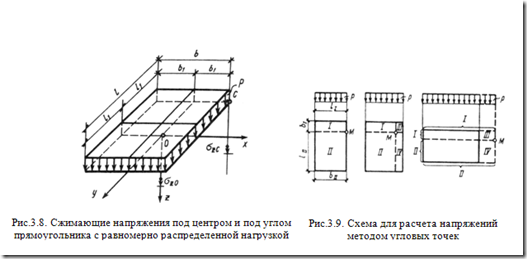



Используя коэффициенты влияния можно записать:

; , (3.11)

где - и - соответственно коэффициенты влияния для угловых и центральных напряжений, зависящие от соотношения сторон загруженного прямоугольника и относительной глубины точки, в которой определяются напряжения.

Между значениями и имеется определенное соотношение.

. (3.12)

Тогда оказывается удобным выразить формулы (3.11) через общий коэффициент влияния и записать их в виде:

; . (3.13)

Коэффициент зависит от безразмерных параметров и : , (при определении углового напряжения ), (при определении напряжения под центром прямоугольника ).

19.Определение напряжений в массиве грунта от действия равномерно-распределенной нагрузки. Метод угловых точек.

Метод угловых точек позволяют определить сжимающие напряжения в основании по вертикали, проходящей через любую точку поверхности. Возможны три варианта решения (рис.3.9.).

Пусть вертикаль проходит через точку , лежащую на контуре прямоугольника. Разделив этот прямоугольник на два так, чтобы точка М являлась угловой для каждого из них, можно представить напряжения как сумму угловых напряжений I и II прямоугольников, т.е.

. (3.13)

Если точка лежит внутри контура прямоугольника, то его следует разделить на четыре части так, чтобы эта точка являлась угловой для каждого составляющего прямоугольника. Тогда:

. (3.14)

Наконец, если точка лежит вне контура загруженного прямоугольника, то его нужно достроить так, чтобы эта точка вновь оказалась угловой.

.

20.Распределение напряжений при плоской задаче. (Задача Фламана).

Схема для расчета напряжений в основании в случае плоской задачи при действии равномерно распределенной нагрузки интенсивностью показана на рис. 3.6.а.

Точные выражения для определения компонент напряжений в любой точке упругого полупространства были получены Г. В. Колосовым в виде:

; ; , (3.9)

где , , - коэффициенты влияния, зависящие от безразмерных параметров и ; и – координатные точки, в которой определяются напряжения; – ширина полосы загружения.

На рис. 3.7. а-в показано в виде изолиний распределение нарпряжении , и в массиве грунте для случая плоской задачи

В некоторых случаях при анализе напряженного состояния основания оказывается удобнее пользоваться главными напряжениями. Тогда значения главных напряжений в любой точке упругого полупространства под действием полосовой равномерно распределенной нагрузки можно определить по формулам И. Х. Митчелла:

, (3.10)

где - угол видимости, образованный лучами, выходящими из данной точки к краям загруженной полосы.

21.Эпюры и изолинии распределения напряжений в массиве грунта.

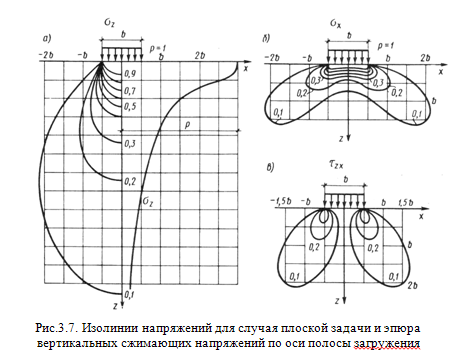
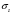Изобары – это линии равных напряжений. К ним относятся изобары – лини равных , распоры – линии равных 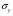и сдвиги – линии равных τ.

0,9p

0,3p

0,2p

b b

р p

2b b b 2b b 2b




0,3p

0,2p

0,1p


0,5p

0000 b

Анализ этих эпюр позволяет сделать выводы:

Грунт, расположенный внутри области, ограниченной изобарой 0,1Р практически обеспечивает восприятие внешней нагрузки. Эта область рассматривается как основание сооружения, т.е. можно считать, что основание ограничено глубиной до 6 b.

Напряженно-деформируемое состояние грунта имеет место за пределами прикладываемой нагрузки.

Области предельных состояний формируются под угловыми точками прикладываемой нагрузки, поскольку в этих точках касательные напряжения достигают предельных значений.