Вопросы-ответы. Строительная механика.. 16. Матричная форма расчёта снс на многовариантные силовые воздействия (общий случай)
 Скачать 449.75 Kb. Скачать 449.75 Kb.
|
|
F K 1 1 F2= 1 K q тельная СОС, рациональная для вычисления углового перемещения, показана на рис. 2.2, в, а соответствующая эпюра единичных изгибающих моментов – на рис. 2.2, г. MF а) б) M1= 1 i0= 1 в) г) д) е) i0= 2 Рис. 2.2 Другая вспомогательная СОС, более выгодная для опреде-ления перемещения точки K, и полученная в ней эпюра момен-тов от единичной силы F2= 1 изображены на рис. 2.2, д и е. Читателю предлагается самостоятельно убедиться в том, что по-пытка использовать схему по рис. 2.2, д для расчёта на M1 = 1 и наоборот приводят к более сложным эпюрам, чем приведены на рис. 2.2, г и е. Вариант с использованием формулы ( 2.3 ) в рассматривае-мой задаче нерационален, так как при незначительном упрощении эпюры мо ментов от нагрузки ( рис. 2.3 ) во вспо- могательной СОС по схеме рис. 2.2, д необходимо дважды рассчитывать СНС на единичные воздействия. Рис. 2.3 В заключение отметим, что в качестве вспомогательной можно использовать не обязательно статически определимую систему, но и любую систему, полученную из рассчитываемой СНС удалением не всех, а части лишних связей. Но эта теоретическая возможность не даёт практической выгоды в сравнении с применением ВСОС. 30. Определение перемещений в СНС от температурных воздействий. Определение перемещений в плоских стержневых СНС от температурных ( тепловых ) воздействий возможно по одной из двух формул, вытекающих из универсальной формулы Макс-велла – Мора: 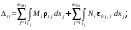 ( 2.4) ( 2.4)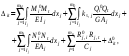 ( 2.5 ) ( 2.5 ) где Mi , Ni – изгибающие моменты и продольные силы в фиктив- ном единичном состоянии рассчитываемой стати- чески неопределимой системы от единичного воз- действия Fi= 1 или Мi= 1 по направлению искомого перемещения; - условно свободные ( нестеснённые ) 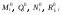 – то же, что на с. 40; – то же, что на с. 40;Mt, Qt, Nt иRj, t – внутренние усилия и реакции упругих свя- зей в действительном состоянии рассчитываемой статически неопределимой системы от заданного изменения температуры, найденные в результа расчёта СНС; -перемещение во вспомогательной СОС от изменения температуры Рис. 2.4 является иллюстрацией к определению перемеще-ний в СНС от изменений температуры двумя описанными выше способами – по ( 2.4 ) и ( 2.5 ). it Fi = 1 Fi = 1 i Nt t i0 а) б) в) t 0t t i г) д) е) Mt ж) з) и) Рис. 2.4 В любом варианте предварительно вычисляются температурные деформации t и 0tдля действительного состояния системы ( рис. 2.4, а ). В случае использования формулы ( 2.4 ) расчётом заданной СНС на единичное воздействие ( рис. 2.4, б ) определяются усилия Mi и Ni ( рис. 2.4, д, з ), «перемножаемые» затем с деформациями t и 0t . При этом определять силовые факторы Mtи Nt в статически неопределимой раме не требуется. Если к моменту определения перемещений СНС уже рассчитана на изменение температуры и в ней найдены моменты и продольные силы, то рациональным может оказаться вычисление перемещений по формуле ( 2.5 ). Для этого выбирается вспомогательная СОС, в которой далее определяются усилия от единичного воздействияFi= 1 ( рис. 2.4, в, е, и ), подставляемые в ( 2.5 ), где первые четыре слагаемых учитывают упругие (силовые) деформации*) ВСОС от внутренних силовых факторов, равных усилиям в действительном состоянии СНС от заданного теплового воздействия. Последний член ( 2.5 ) – вклад в искомое перемещение температурных деформаций элементов ВСОС. Замечание: руководствуясь при выборе вспомогательной СОС рекомендациями, изложенными на с. 41, можно также дополнительно добиваться равенства нулю единичных усилий хотя бы на некоторых участках температурных воздействий. 31. Определение перемещений в СНС от смещений связей. Для определения перемещений, вызванных смещениями связей ( кинематическими воздействиями ) в статически неопределимых системах, служат формулы 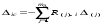 ( 2.6 ) ( 2.6 )И ( 2.7 ) где R(j), i – реакции связей, по направлениям которых имеются за- данные смещения (j) ( j = 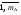 ), в фиктивном единич- ), в фиктивном единич-ном состоянии рассчитываемой статически неопре- делимой системы от единичного воздействия Fi= 1 или Мi= 1 по направлению искомого перемещения ( поло- жительной считается реакция Rj),i, направленная в ту же сторону, что и соответствующее смещение j)); m – число компонентов заданных смещений связей; 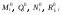 – то же, что на с. 40; – то же, что на с. 40;Mc, Qc, Nc и Rj, c – внутренние усилия и реакции упругих свя- зей в действительном состоянии рассчитываемой ста- тически неопределимой системы от заданных смеще- ний связей, найденные в результате расчёта СНС; – перемещение во вспомогательной СОС отсмещений На рис. 2.5 схематично показаны оба способа определения перемещения от кинематического воздействия ( смещения одной из опор рамы ). ic Fi = 1 Fi = 1 i а) б) в) i i0 Rj+1),i 0 c j) Rj),i j+1) г) д) Mc Рис. 2.5 В случае использования формулы ( 2.6 ) из действительного состояния ( рис. 2.5, а ) берутся только значения заданных компонентов смещений опор ( никаких вычислений не требуется ), а из результатов расчёта СНС на единичное воздействие ( рис. 2.5, б ) – лишь реакции смещаемых связей ( напоминаем, что положительной считается реакция Rj),i, направленная в ту же сторону, что и соответствующее смещение j)). При определении перемещения с помощью вспомогательной СОС ( рис. 2.5, в ) учитываются внутренние усилия ( здесь – моменты 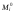 ), входящие в интегралы формулы ), входящие в интегралы формулы ( 2.7 ), и реакции 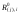 смещаемых связей, с помощью которых вычисляется перемещение смещаемых связей, с помощью которых вычисляется перемещение 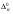 . Заметим, что если бы была выбрана консольная . Заметим, что если бы была выбрана консольнаяВСОС по схеме рис. 2.4, в, то все единичные реакции смещаемых связей оказались бы равными нулю, тогда 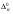 = 0. = 0. Как и в случаях двух других видов воздействий ( силовых и тепловых ), применение вспомогательной СОС в этой задаче рационально, если силовые факторы Sc, Rj, c и R(j), c ранее найдены расчётом СНС на кинематическое воздействие. |
