Вопросы-ответы. Строительная механика.. 16. Матричная форма расчёта снс на многовариантные силовые воздействия (общий случай)
 Скачать 449.75 Kb. Скачать 449.75 Kb.
|
21.2. Группировка линейных перемещений узловГруппировка линейных перемещений симметрично расположенных узлов целесообразна, если при выборе основной системы метода перемещений наложение линейных связей на узлы производится без нарушения симметрии сооружения. 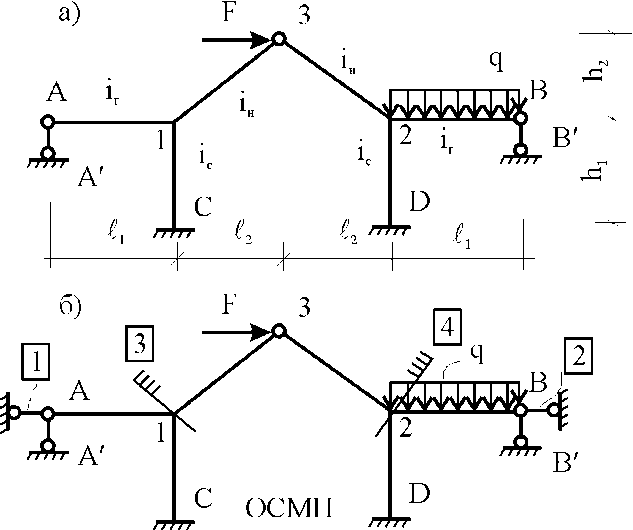 Рис. 21.3 Поясним это на примере рамы, имеющей вертикальную ось симметрии (рис. 21.3,а). Степень кинематической неопределимости этой рамы равна четырем (nθ = 2, nΔ = 2). Для ее расчета предлагается симметричная основная система метода перемещений, показанная на рис. 21.3,б. Рассмотрим группировку линейных перемещений узлов А и В рамы, приняв за неизвестные групповые линейные перемещения, а именно: сумму 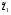 и разность и разность 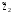 линейных перемещений этих узлов Z1 и Z2, т.е. линейных перемещений этих узлов Z1 и Z2, т.е.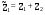 , , 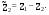 В единичном состоянии основной системы метода перемещений неизвестному групповому перемещению 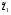 соответствует одновременное смещение линейных связей 1 и 2, наложенных на узлы А и В, направо на величину, равную единице, другими словами, обратно симметричная деформационная схема элементов рамы и обратно симметричная групповая эпюра изгибающих моментов соответствует одновременное смещение линейных связей 1 и 2, наложенных на узлы А и В, направо на величину, равную единице, другими словами, обратно симметричная деформационная схема элементов рамы и обратно симметричная групповая эпюра изгибающих моментов 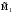 (рис. 21.4). (рис. 21.4).Неизвестному групповому перемещению 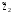 в основной системе метода перемещений соответствует одновременное единичное смещение связей 1 и 2 в разные стороны, т.е. симметричная деформационная схема и симметричная групповая эпюра изгибающих моментов в основной системе метода перемещений соответствует одновременное единичное смещение связей 1 и 2 в разные стороны, т.е. симметричная деформационная схема и симметричная групповая эпюра изгибающих моментов  (рис. 21.5). (рис. 21.5).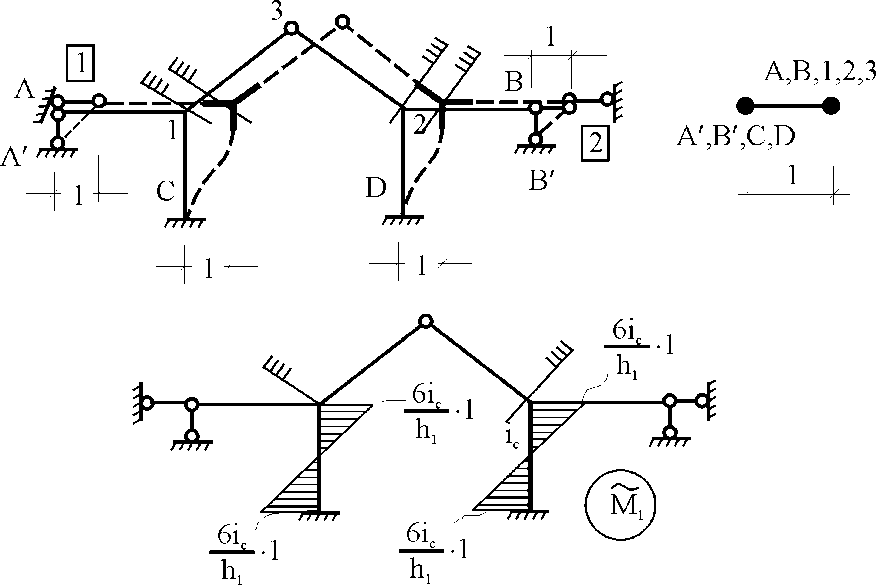 Рис. 21.4 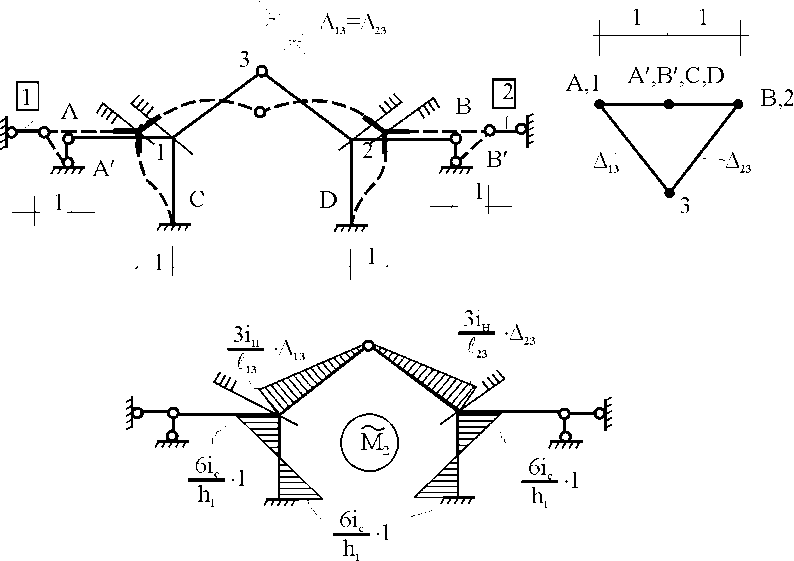 Рис. 21.5 Учитывая обратно симметричный характер групповой эпюры изгибающих моментов  и симметричный – и симметричный – , получим , получим Следствием группировки линейных и угловых перемещений симметрично расположенных узлов сооружения является упрощение системы канонических уравнений метода перемещений за счет исключения из нее нулевых побочных коэффициентов. 26. Использование прямой и обратной симметрии внешних воздействий в расчётах симметричных СНС методом перемещений. 27. Расчёт СНС методом перемещений на температурные воздействия.  В плоской n раз кинематически неопределимой стержневой системе краевые волокна всех или части элементов испытывают воздействие температурного поля (рис. 20.4,а). Характеристиками этого поля для k-го стержня сооружения являются: перепад приращения температуры по высоте поперечного сечения В плоской n раз кинематически неопределимой стержневой системе краевые волокна всех или части элементов испытывают воздействие температурного поля (рис. 20.4,а). Характеристиками этого поля для k-го стержня сооружения являются: перепад приращения температуры по высоте поперечного сечения  и приращение температуры на уровне его центра тяжести и приращение температуры на уровне его центра тяжести  (см. п. 20.1 настоящей лекции). (см. п. 20.1 настоящей лекции).Наложением n угловых и линейных связей образуем основную систему метода перемещений заданного сооружения (рис. 20.4,б). Неизвестные угловые и линейные перемещения его узлов Z1, Z2,…, Zi,…, Zj,…, Zn определим из условий равенства нулю реакций в наложенных связях от их смещения на величины Z1, Z2,…, Zi,…, Zj,…, Zn и от заданного изменения температуры. Используя принцип независимости действия сил и повторяя выкладки, приведенные в п. 19.3 девятнадцатой лекции, получим систему канонических уравнений метода перемещений для определения неизвестных Z1, Z2,…, Zi,…, Zj,…, Zn в случае температурного воздействия на сооружение  (20.2) (20.2)Величины главных rii и побочных rij коэффициентов системы уравнений (20.2) не зависят от вида воздействия на сооружение и определяются по-прежнему (см. п. 19.5 девятнадцатой лекции). Свободные члены системы канонических уравнений (20.2) Rit – это реакции в i-х наложенных связях от изменения температуры в основной системе метода перемещений. Они определяются по эпюрам внутренних усилий (в рамках и балках – по эпюрам изгибающих моментов), построенным в основной системе от температурного воздействия статическим способом, т.е. из условий равновесия узлов и отдельных частей сооружения. Эпюра изгибающих моментов  от изменения температуры в основной системе метода перемещений складывается из двух эпюр: от изменения температуры в основной системе метода перемещений складывается из двух эпюр:  – от неравномерных приращений температуры и эпюры – от неравномерных приращений температуры и эпюры  – от равномерных. – от равномерных.Для построения эпюры изгибающих моментов  от неравномерных приращений температуры от неравномерных приращений температуры  используются стандартные задачи, приведенные в п. 20.1 настоящей лекции (см. рис. 20.2,д и 20.3,а). используются стандартные задачи, приведенные в п. 20.1 настоящей лекции (см. рис. 20.2,д и 20.3,а).Равномерное приращение температуры  в основной системе метода перемещений вызывает линейные смещения узлов сооружения и, следовательно, перекосы его элементов, численные значения которых можно получить, используя план перемещений. В данном случае при построении этого плана необходимо учитывать продольные перемещения стержней, вызванные их равномерным нагреванием или охлаждением. Зная перекосы стержней, эпюру изгибающих моментов в основной системе метода перемещений вызывает линейные смещения узлов сооружения и, следовательно, перекосы его элементов, численные значения которых можно получить, используя план перемещений. В данном случае при построении этого плана необходимо учитывать продольные перемещения стержней, вызванные их равномерным нагреванием или охлаждением. Зная перекосы стержней, эпюру изгибающих моментов  в основной системе метода перемещений построим с помощью стандартных задач, полученных от линейных кинематических воздействий (см. рис. 19.9 и 19.10). в основной системе метода перемещений построим с помощью стандартных задач, полученных от линейных кинематических воздействий (см. рис. 19.9 и 19.10).Окончательную эпюру изгибающих моментов Mt в заданном сооружении от температурного воздействия после решения системы уравнений (20.2) получим, используя соотношение:  (20.3) (20.3)В формуле (20.3)  = = + + . .Эпюры поперечных и продольных сил Qt и Nt построим по эпюре изгибающих моментов Mt , используя условия равновесия отдельных элементов и узлов заданного сооружения. Эпюры внутренних усилий Mt, Qt и Nt, полученные методом перемещений, построены правильно, если выполнена статическая проверка решения задачи, т.е. если все узлы и любые части заданного сооружения находятся в равновесии. 28. Расчёт СНС методом перемещений на кинематические воздействия. В плоской n раз кинематически неопределимой стержневой системе (рис. 20.12,а) m угловых и линейных опорных связей получили смещения, численные значения которых соответственно равны Δ(1), Δ(2),…,Δ(m). По-прежнему изгибные жесткости поперечных сечений элементов сооружений будем считать постоянными. 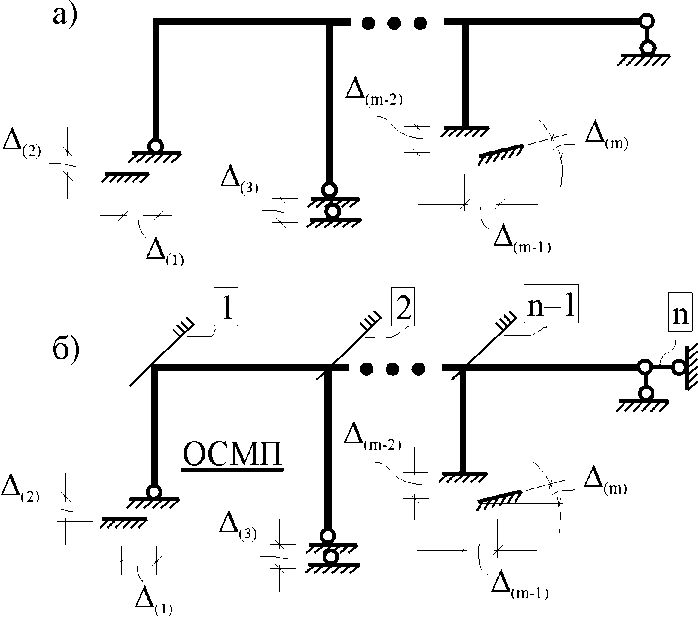 Рис. 20.12 Наложением n угловых и линейных связей на узлы сооружения образуем основную систему метода перемещений (рис. 20.12,б). Неизвестные перемещения узлов Z1, Z2,…, Zi,…, Zj,…, Zn определим, отрицая в основной системе реакции в наложенных связях от их смещения на величины Z1, Z2,…, Zi,…, Zj,…, Zn и от заданного кинематического возмущения опорных связей, т.е. из системы канонических уравнений 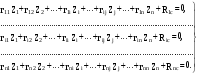 (20.5) (20.5)Физический смысл коэффициентов при неизвестных и способы их определения подробно рассмотрены ранее (см. п. 19.3 и п. 19.5 девятнадцатой лекции). Свободные члены Ric системы уравнений (20.5) – это реакции в i-х наложенных связях в основной системе метода перемещений от заданного смещения опорных связей. В рамах и балках они определяются статическим способом по эпюре изгибающих моментов  , построенной в основной системе метода перемещений от заданных кинематических воздействий. Для построения эпюры изгибающих моментов , построенной в основной системе метода перемещений от заданных кинематических воздействий. Для построения эпюры изгибающих моментов 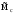 используются стандартные задачи, рассмотренные в п. 19.4 девятнадцатой лекции (см. рис. 19.9 и 19.10). используются стандартные задачи, рассмотренные в п. 19.4 девятнадцатой лекции (см. рис. 19.9 и 19.10).После решения системы уравнений (20.5) окончательную эпюру изгибающих моментов Мс в заданном сооружении от смещения опорных связей получим, используя принцип независимости действия сил: 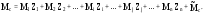 (20.6) (20.6)Решение задачи завершается построением эпюр поперечных и продольных сил Qc и Nc по известной эпюре изгибающих моментов Мс и статической проверкой правильности расчета. 29. Определение перемещений в СНС от силовых воздействий. В инженерных расчётах строительных конструкций кроме усилий, необходимых для оценки прочности, требуется определять также характерные перемещения для проверки выполнения требований по жёсткости. Для вычисления перемещений в статически неопредели-мой стержневой системе в общем случае комбинации силовых, тепловых и кинематических воздействий ( на рис. 2.1, а показано действительное ( ) состояние СНС ) можно использовать уни-версальную формулу Максвелла – Мора в форме ( 1.12 ) или ( 1.14 ) для плоских систем. q F а) б) Fi = 1 a a i i i t i a' ( j) в) г) Si SF Рис. 2.1 Следует иметь в виду, что в рассматриваемой задаче о перемещениях в СНС входящие в указанные формулы силовые факторы SF и Rj, F – это внутренние усилия и реакции упругих связей в действительном состоянии рассчитываемой статически неопределимой системы от заданных нагрузок ( на рис. 2.1, в в качестве иллюстрации усилий SF показана эпюра изгибающих моментов ). ВместоSF и Rj, F могут использоваться суммарные силовые факторы S и Rj, от всех воздействий, включая температурные и смещения связей ( в разделе 1 эти силовые факторы – результаты расчёта – обозначались S и Rj*)), – будет получено то же значение искомого перемещения. Иной смысл, чем в методе сил, имеют единичные усилия и реакции упругих связей Si и Rj, i– они определяются в статически неопределимой системе от единичного воздействия – силы Fi= 1 или момента Мi= 1 по направлению подлежащего определению линейного или углового перемещения ( рис. 2.1, б, г ). Таким образом, для отыскания одного перемещения в СНС по общей формуле метода Максвелла – Мора необходимо выполнить расчёт СНС дважды – на заданные воздействия действительного состояния ( ) и на единичное силовое воздействие фиктивного состояния ( i ). Вычисление каждого следующего перемещения требует нового расчёта СНС на соответствующую фиктивную единичную нагрузку. При компьютерном расчёте СНС в матричной форме эти фиктивные нагрузки рассматриваются как дополнительные варианты при формировании матрицы L ( см. с. 26 ). «Перемножение» усилий SF и Si «вручную» при вычислении интегралов в формуле Максвелла – Мора может быть трудоёмким из-за того, что от любого воздействия внутренние силовые факторы возникают, как правило, во всех элементах СНС. Если учесть особые свойства СНС и использовать в расчете их перемещений вспомогательные статически определимые системы, то точные результаты могут быть получены значительно проще – объяснения и формулы даны ниже. *) Необходимо уяснить, что символы и обозначения общей теории определения перемещений не имеют никакого отношения к исполь- зуемым в методе сил «внутренним» одноимённым величинам. 2.1. Определение перемещений от силовых воздействий Альтернативными вышеупомянутому способу вычисления перемещений, который для случая силовых воздействий в плос-кой стержневой СНС даёт формулу 57 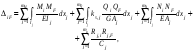 ( 2.1 ) ( 2.1 )являются выражения 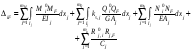 ( 2.2 ) ( 2.2 )и 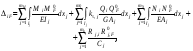 (2.3 ) (2.3 )где 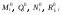 – внутренние усилия и реакции упругих – внутренние усилия и реакции упругихсвязей во вспомогательной статически определимой системе от единичного воз- действия Fi= 1 или Мi= 1 по направлению искомого перемещения; 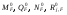 – внутренние усилия и реакции упругих – внутренние усилия и реакции упругихсвязей во вспомогательной статически определимой системе от заданной нагруз- 58 ки. Вариант ( 2.2 ) рационален, если вычисление перемещений выполняется после расчёта СНС на заданную нагрузку, когда уже найдены силовые факторы MF, QF, NF и Rj, F . Использование формулы ( 2.3 ) выгодно в тех случаях, ко-гда по каким-либо причинам усилия в рассматриваемой СНС от заданной нагрузки находить не требуется, а нужны только перемещения. 59 Вспомогательная статически определимая система ( ВСОС ) получается из заданной СНС удалением лишних связей. При её выборе рекомендуется руководствоваться следующим: 1) вспомогательная СОС должна быть такой, чтобы усилия в ней от единичного фиктивного воздействия ( в случае исполь-зования формулы ( 2.2 )) или от заданной нагрузки ( по варианту ( 2.3 )) возникали бы на минимально возможном числе участков; 2) если требуется найти несколько перемещений, то для определения каждого из них по формуле ( 2.2 ) целесообразно использовать свою вспомогательную СОС, рациональную в рас-чёте на соответствующее единичное воздействие Fi= 1 ( дающую наиболее компактное распределение единичных усилий ). 3) если при реализации варианта ( 2.2 ) расчёт СНС на за-данную нагрузку выполнен методом сил, то ВСОС выбирается независимо от того, какая статически определимая система была использована в качестве основной системы метода сил*). Способ выполнения рекомендаций 1 и 2 в случае вычисления перемещения по ( 2.2 ): если это допускает структура заданной СНС, то вспомогательную СОС выгодно выбирать так, чтобы сечение (точка) с подлежащим определению перемещением оказывалось на главной части ВСОС. Частный случай: если вблизи от места с определяемым перемещением имеется опорное защемление, то во вспомогательной СОС его целесооб-разно сохранить. Комментарий к п. 3: в качестве ВСОС может использоваться СОС, совпадающая по структуре с ОСМС в расчёте на заданную нагрузку, но это не всегда удачное решение, так как выбор рациональных ОСМС и ВСОС производится по принципиально разным соображениям ( ср. вышеприведённый п. 1 с п.п. 1, 2, 5 на с. 8, 9 ). Кроме того, использованная ОСМС – единственная, а вспомогательных СОС, согласно п. 2, может быть несколько. На рис. 2.2 приведён пример выбора вспомогательных ста-тически определимых систем при определении угла поворота сечения 1 и вертикального перемещения точки K рамы, расчёт которой на действие равномерно распределённой нагрузки q дал эпюру моментов MF , представленную на рис. 2.2, б. Вспомога- *) Не следует отождествлять вспомогательную СОС с ОСМС, так как последняя ассоциируется с основными неизвестными метода, которых во вспомогательной СОС вообще нет. |
