Вопросы-ответы. Строительная механика.. 16. Матричная форма расчёта снс на многовариантные силовые воздействия (общий случай)
 Скачать 449.75 Kb. Скачать 449.75 Kb.
|
21.2. Группировка угловых перемещений узловРассмотрим расчет рамы с вертикальной осью симметрии на произвольную нагрузку (рис. 21.1,а). Соотношение между погонными жесткостями симметрично расположенных ригелей 1А, 2В 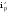 и стоек 1С, 2D ic, а также центрального ригеля 12 и стоек 1С, 2D ic, а также центрального ригеля 12 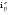 , задано. Степень кинематической неопределимости рамы равна двум. На рис. 21.1,б показана основная система метода перемещений для этой рамы. , задано. Степень кинематической неопределимости рамы равна двум. На рис. 21.1,б показана основная система метода перемещений для этой рамы.Неизвестные углы поворотов узлов 1 и 2 рассма триваемой рамы от заданной нагрузки Z1 и Z2 определяются из системы канонических уравнений (см. п. 19.3 девятнадцатой лекции) 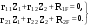 (21.1) (21.1)Нетрудно убедиться в том, что в нашем случае, принимая за неизвестные углы поворота отдельных узлов, мы будем иметь полную систему уравнений (21.1), т.е. ни один из коэффициентов при неизвестных Z1 и Z2 не будет равен нулю (предлагаем читателям самостоятельно проверить это). Используем симметрию рамы и произведем группировку угловых перемещений симметрично расположенных узлов 1 и 2. Каждое из уравнений системы (21.1) отрицает в основной системе метода перемещений реакции R1 и R2 в наложенных угловых связях 1 и 2 от их поворота на углы, равные Z1 и Z2, и от заданной нагрузки, т.е. первое уравнение удовлетворяет условию R1 = 0, а второе – R2 = 0. Эти условия будут выполнены, если в основной системе метода перемещений будем одновременно отрицать разность и сумму реакций в наложенных связях 1 и 2, т.е. если будем отрицать групповые реакции 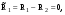 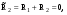 Групповым реакциям 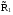 и и 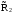 соответствуют групповые угловые перемещения узлов 1 и 2 соответствуют групповые угловые перемещения узлов 1 и 2 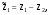 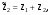 которые в дальнейшем будем называть групповыми неизвестными метода перемещений. которые в дальнейшем будем называть групповыми неизвестными метода перемещений.В единичном состоянии основной системы метода перемещений неизвестному групповому перемещению 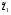 соответствует одновременный поворот угловой связи, наложенной на узел 1, по часовой стрелке на угол, величина которого равна единице, и угловой связи, наложенной на узел 2, – против часовой стрелки на такой же угол – другими словами, симметричная деформационная схема элементов рамы и симметричная групповая эпюра изгибающих моментов соответствует одновременный поворот угловой связи, наложенной на узел 1, по часовой стрелке на угол, величина которого равна единице, и угловой связи, наложенной на узел 2, – против часовой стрелки на такой же угол – другими словами, симметричная деформационная схема элементов рамы и симметричная групповая эпюра изгибающих моментов 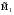 (рис. 21.1,в,г). Аналогично, групповому неизвестному перемещению (рис. 21.1,в,г). Аналогично, групповому неизвестному перемещению 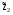 в основной системе метода перемещений соответствует обратно симметричная схема деформаций и обратно симметричная групповая эпюра изгибающих моментов в основной системе метода перемещений соответствует обратно симметричная схема деформаций и обратно симметричная групповая эпюра изгибающих моментов 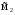 (рис. 21.1,д,е). (рис. 21.1,д,е).При построении групповых эпюр изгибающих моментов 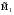 и и 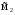 для всех элементов рамы, кроме центрального ригеля 12, использованы стандартные задачи метода перемещений, рассмотренные в п. 19.4 девятнадцатой лекции. На ригеле 12 эпюры изгибающих моментов можно получить суммированием соответствующих эпюр от симметричного поворота двух угловых связей на угол θ (рис. 21.2,а) и от обратно симметричного поворота этих же связей на такой же угол (рис. 21.2,б). для всех элементов рамы, кроме центрального ригеля 12, использованы стандартные задачи метода перемещений, рассмотренные в п. 19.4 девятнадцатой лекции. На ригеле 12 эпюры изгибающих моментов можно получить суммированием соответствующих эпюр от симметричного поворота двух угловых связей на угол θ (рис. 21.2,а) и от обратно симметричного поворота этих же связей на такой же угол (рис. 21.2,б).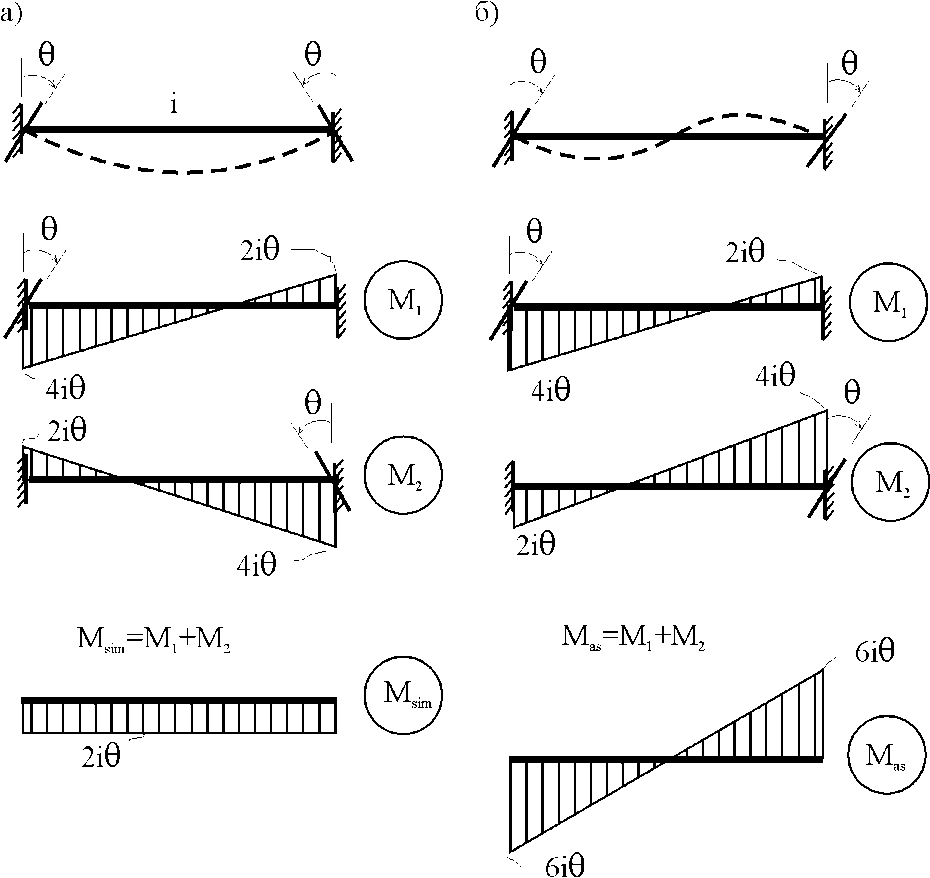 Рис. 21.2 Система канонических уравнений (21.2) для групповых неизвестных метода перемещений перепишется: 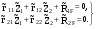 (21.2) (21.2)Коэффициенты при неизвестных 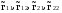 и свободные члены и свободные члены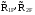 системы уравнений (21.2) можно вычислить сопряжением соответствующих эпюр изгибающих моментов (см. формулы (19.11), (19.12) и (19.18) девятнадцатой лекции), либо из условия равновесия одновременно двух узлов, содержащих симметрично расположенные связи. системы уравнений (21.2) можно вычислить сопряжением соответствующих эпюр изгибающих моментов (см. формулы (19.11), (19.12) и (19.18) девятнадцатой лекции), либо из условия равновесия одновременно двух узлов, содержащих симметрично расположенные связи.Так как групповые эпюры 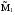 и и 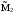 носят соответственно симметричный и обратно симметричный характер, то носят соответственно симметричный и обратно симметричный характер, то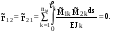 С учетом последнего обстоятельства система уравнений (21.2) распадается на два независимых друг от друга уравнения: 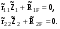 При построении эпюр внутренних усилий в заданном сооружении групповые неизвестные метода перемещений используются как обычные. В частности, для рамы, показанной на рис. 21.1,а имеем: 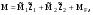 где MF – эпюра изгибающих моментов в основной системе метода перемещений от заданной нагрузки. |
