Вопросы-ответы. Строительная механика.. 16. Матричная форма расчёта снс на многовариантные силовые воздействия (общий случай)
 Скачать 449.75 Kb. Скачать 449.75 Kb.
|
16. Матричная форма расчёта СНС на многовариантные силовые воздействия (общий случай). .Матричная форма расчета статически неопределимых систем методом перемещенийСистему канонических уравнений метода перемещений (19.6) представим в матричной форме: rZ + R = 0. (22.21) r – матрица коэффициентов при неизвестных системы канонических уравнений (22.21), или матрица реакций в наложенных связях от их смещения на величину, равную единице, в основной системе метода перемещений. Эта матрица называется матрицей внешней жесткости сооружения. 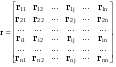 Число строк и столбцов матрицы внешней жесткости сооружения равно степени его кинематической неопределимости nkin, т.е. матрица r – квадратная матрица. В силу теоремы о взаимности реакций матрица r симметрична. Так как система уравнений (22.21) разрешима, то определитель матрицы r не равен нулю (det r ≠ 0). Это значит, что матрица внешней жесткости является невырожденной матрицей. Z – матрица неизвестных метода перемещений, или матрица угловых и линейных перемещений узлов сооружения от заданных внешних воздействий (силовых, температурных, кинематических). 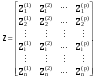 R – матрица свободных членов системы канонических уравнений метода перемещений (22.21), или матрица реакций в наложенных связях от заданных внешних воздействий в основной системе метода перемещений.  Число строк в матрицах Z и R равно степени кинематической неопределимости сооружения, а число столбцов – суммарному числу заданных независимых силовых, температурных и кинематических воздействий на сооружение. В п. 22.2 настоящей лекции на базе теоремы о работе концевых усилий были получены матричные соотношения (22.16) и (22.20) для вычисления элементов матриц r и R. Напомним их: 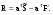 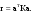 Смысл элементов матриц, включенных в формулы (22.16) и (22.20) подробно изложен в п. 22.2 и 22.3 двадцать второй лекции. Решая систему уравнений (22.21), получим матрицу неизвестных метода перемещений: 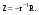 (22.22) (22.22)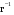 – матрица, обратная по отношению к матрице внешней жесткости сооружения. – матрица, обратная по отношению к матрице внешней жесткости сооружения.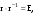 где E – единичная матрица. После подстановки соотношений (22.16) и (22.20) в матричное выражение (22.22) получим: 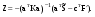 (22.23) (22.23)Используем принцип независимости действия сил для определения концевых усилий в элементах заданного сооружения при силовых, температурных и кинематических воздействиях:  (22.24) (22.24)m – число концевых усилий (концевых изгибающих моментов и концевых поперечных сил), определяемых при решении конкретной задачи. Группа соотношений (22.24) в матричной форме перепишется: 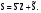 (22.25) (22.25)S – матрица концевых усилий элементов заданного сооружения от внешних силовых, температурных и кинематических воздействий. 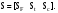 Напомним, что 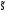 – это матрица концевых усилий элементов сооружения в основной системе метода перемещений от внешних силовых, температурных и кинематических воздействий, а матрица – это матрица концевых усилий элементов сооружения в основной системе метода перемещений от внешних силовых, температурных и кинематических воздействий, а матрица 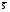 – матрица концевых усилий в основной системе метода перемещений от единичных смещений наложенных связей (см. п. 22.2). – матрица концевых усилий в основной системе метода перемещений от единичных смещений наложенных связей (см. п. 22.2).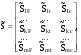 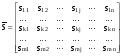 Ранее было показано, что матрица 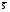 выражается через матрицу внутренней жесткости сооружения K и матрицу перемещений концевых сечений стержней в основной системе от единичных смещений наложенных связей a (см. п. 22.2) следующим образом: выражается через матрицу внутренней жесткости сооружения K и матрицу перемещений концевых сечений стержней в основной системе от единичных смещений наложенных связей a (см. п. 22.2) следующим образом: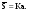 После подстановки матричных выражений (22.18) и (22.23) в матричную формулу (22.25) получим матричное соотношение для расчета стержневых систем методом перемещений 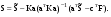 (22.26) (22.26)При силовом воздействии на сооружение, когда S = SF, 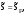 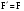 , структура матричной зависимости (22.26) сохраняется: , структура матричной зависимости (22.26) сохраняется: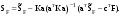 (22.27) (22.27)В случае температурного воздействия S = St, 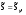 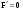 и, следовательно, и, следовательно,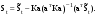 (22.28) (22.28)При кинематическом воздействии, в частности, при смещении опорных связей, матричная зависимость для определения концевых усилий в стержнях заданного сооружения аналогична матричной зависимости (22.28): 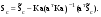 (22.29) (22.29)Проверка правильности расчета заданного сооружения методом перемещений производится на основе теоремы о работе концевых усилий. Подставив значения концевых усилий S, вычисленных по формуле (22.26), в матричное выражение (22.15), мы должны получить нулевые значения реакций в несуществующих в заданном сооружении наложенных связях. Таким образом, в общем случае внешних воздействий имеем: 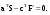 (22.30) (22.30)Матричное соотношение (22.30) при силовых воздействиях перепишется: 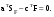 (22.31) (22.31)В случае температурных или кинематических воздействий в матричной зависимости (22.30) следует принять S = St или S = Sс, 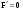 . Проверочные матричные соотношения для этих видов внешних воздействий примут вид: . Проверочные матричные соотношения для этих видов внешних воздействий примут вид: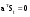 или или 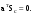 Матричная форма расчёта статически неопределимых систем методом сил Матричная запись канонических уравнений метода сил имеет вид ( 1.7 ): 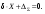 Значения n перемещений в статически неопределимой системе от v вариантов заданных комбинированных воздействий ( с силовыми, тепловыми и кинематическими составляющими ) можно записать в виде матрицы  ( 2.8 ) ( 2.8 )где f = 1, 2, …, v – номер варианта воздействий; i = 1, 2, …, n – номер искомого перемещения. Для определения этих перемещений методом Максвелла – Мора служит матричная формула 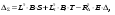 ( 2.9 ) ( 2.9 )где L, Lt и R – матрицы усилий в упруго деформируемых эле- ментах и связях, на участках с температурными деформациями и реакции смещаемых связей в единичных состояниях заданной статически не- определимой системы от фиктивных воздействий Fi 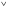 Mi = 1 ( i= Mi = 1 ( i=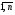 ) по направлениям искомых пе- ) по направлениям искомых пе-ремещений; B и Bt – матрицы внутренней упругой и температурной податливостей; Е = diag [ 1 1 … 1 ]; S – матрица внутренних усилий и реакций упругих связей в статически неопределимой системе от заданных воздействий ( результаты расчёта СНС по вариантам f = 1, 2, …, v ); вместо Sможно ис- пользовать SF ( только от силовых воздействий ); Т и – матрицы приращений температур и заданных смещений связей по вариантам воздействий. Объединение матриц, входящих в ( 2.9 ), даёт выражение 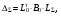 ( 2.10 ) ( 2.10 )где 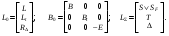 Если матрицу L формировать в виде L = diag [ S T ], то матрица искомых перемещений будет = [ F t c ] – с разделением результатов по видам воздействий. Приведём далее матричные формулы для вычисления перемещений отдельно от силовых, температурных и кинематических воздействий по всем изложенным выше вариантам, в том числе с использованием вспомогательных статически определимых систем ( матричные аналоги выражений ( 2.1 ) – ( 2.7 )): – вариант а, ( 2.11 ) – вариант б, ( 2.12 ) – вариант в, ( 2.13 )  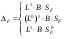 – вариант а, ( 2.14 ) – вариант б, ( 2.15 ) 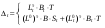 – вариант а, ( 2.16 ) – вариант б, ( 2.17 ) 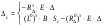 где L0, 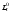 и и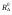 – матрицы усилий в упруго деформируемых эле- – матрицы усилий в упруго деформируемых эле-ментах и связях, на участках с температурными деформациями и реакции смещаемых связей в единичных состояниях вспомогательной статиче- ски определимой системы от фиктивных воздей- ствий Fi 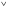 Mi = 1 ( i= Mi = 1 ( i=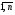 ) по направлениям иско- ) по направлениям иско-мых перемещений; SF , St и Sc – матрицы внутренних усилий и реакций упругих связей в статически неопределимой системе от заданных силовых, температурных и кинемати- ческих воздействий. 17. Понятие о кинематически неопределимых системах Деформируемая система, у расчётных узлов которой есть неизвестные угловые и/или линейные перемещения, не находящиеся из условий совместности деформаций ( перемещений ) и кинематических граничных условий, называется кинематически неопределимой системой. Система, у которой все угловые и линейные перемещения расчётных узлов известны ( заданы либо равны нулю ) или могут быть найдены из условий совместности деформаций ( перемещений ) и кинематических граничных условий, называется кинематически определимой системой. 18. Расчётные узлы кинематически неопределимой системы. Степень кинематической неопределимости. Расчётными узлами являются: 1) места соединения двух и более элементов или точки перелома оси ломаного стержня ( рис. 1.2, а – г ); 2) точки изменения значения или типа жёсткости сечения стержня ( рис. 1.2, д, е ); 3) опорные узлы с неизвестными компонентами перемещений ( рис. 1.2, ж – и ); 4) дополнительно – любые точки системы ( рис. 1.2, к ). с а) б) в) г) д) EI2 EI1 е)   ж) з) и) ж) з) и)u с v с к) л) Рис. 1.2 Суммарное число независимых угловых и линейных перемещений расчётных узлов называется степенью кинематической неопределимости деформируемой системы: nk = n + n , ( 1.1 ) где n и n – соответственно степени угловой и линейной подвижности расчётных узлов (количества их независимых угловых и линейных перемещений). Число угловых основных неизвестных n определяется через число жёстких расчётных узлов nж.у.: 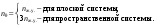 ( 1.2 ) ( 1.2 )Если в системе есть упругие угловые свя- зи, то число стержней, ими соединяемых, фор- мально включается в nж.у.. Например, для ком- Рис. 1.4 бинированного узла на рис. 1.2, г nж.у. = 2. Для узла, показанного на рис. 1.4, nж.у. = 4. рабочая гипотеза: для прямолинейных стержневых элементов с преобладающим изгибом можно считать пренебрежимо малым изменение расстояния между концами стержня, обусловленное а) искривлением элемента при его изгибе и б) удлинением ( укорочением ) при растяжении ( сжатии ). Краткая формулировка гипотезы: длина l* хорды b*e* деформированного элемента считается равной длине l стержня beв исходном – недеформированном – состоянии ( рис. 1.5 ): l 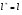 . ( 1.4 ) . ( 1.4 ) b e Следствием применения гипотезы ( 1.4 ) b* к некоторому стержню является то, что для e* узлов, к которым данный элемент примыкает l* своими концами, он может рассматриваться Рис. 1.5 как жёсткая линейная связь между этими узлами. Из-за этого некоторые перемещения узлов перестают быть независимыми, и степень линейной подвижности узлов уменьшается. Для определения n удобно использовать вспомогательную шарнирную систему, получаемую из рассчитываемой системы путём а) введения цилиндрических шарниров ( в пространственной системе – шаровых шарниров ) во все жёсткие узлы, включая опорные защемления; а также продольных поступательных шарниров в стержни, для которых требуется учитывать удлинения ( укорочения ) при их растяжении ( сжатии ); б) удаления угловых и линейных упругих связей ( при их наличии ), в том числе опорных. Шарнирная система ( ШС ), получаемая в результате удаления связей, может быть изменяемой. Минимальное число nд.с. линейных связей, дополнительное введение которых в узлы ШС превращает её в геометрически неизменяемую, равно искомой степени линейной подвижности расчётных узлов n заданной (рассчитываемой) системы: n = nд.с.. Число степеней свободы изменяемой шарнирной системы, для устранения которых требуется ввести соответствующее количество связей n, может вычисляться как WШС с использованием формулы для фермы: 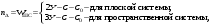 ( 1.6 ) ( 1.6 )где У, С и С0 – количества узлов, стержней и опорных связей ( в пересчёте на связи 1-го типа) шарнирной системы. При подсчёте числа стержней С элементы ШС с поступательными шарнирами не учитываются. Следует иметь в виду, что если в шарнирной системе имеются статически неопределимые части, то определение n по формуле ( 1.6 ) может давать ошибку. 19. Основная система метода перемещений (ОСМП), правила её формирования с учётом и без учёта продольных деформаций элементов. Основная система метода перемещений ( ОСМП ) – это, как правило, кинематически определимая система, получаемая из заданной деформируемой системы путём введения в расчётные узлы минимально необходимых жёстких угловых и линейных связей по направлениям перемещений, принимаемых за основные неизвестные. Угловые связи вводятся в жёсткие ( в т.ч. условно жёсткие ) узлы и устраняют возможность их поворотов, не препятствуя линейным перемещениям. узле осуществляется так, как показано на рис. 1.14, а. Её упрощённое изображе- а) б) ние дано на рис. 1.14, б. Расположение угловых Рис. 1.14 связей не имеет вариантов ( единственное ). Дополнительные линейные связи, вводимые в расчётные узлы, предназначены для закрепления их от возможных линей- ных смещений. Связи могут располагаться так же, как в шарнирной системе, если она использовалась на стадии выявления степени кинематической неопределимости. В случае расчёта с учётом всех видов деформаций ( если допущение 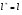 не применяется ) элементы основной системы не применяется ) элементы основной системыпри любых заданных воздействиях деформируются независимо друг от друга, а при смещении какой-либо из дополнительных связей, введённых в расчётные узлы, деформации испытывают лишь те элементы, которые примыкают к смещаемому узлу ( при этом должны удовлетворяться условия совместности перемещений их концевых сечений в узле ). Если в расчёте используется гипотеза 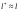 , то , то а) при силовых воздействиях элементы ОСМП в отношении изгиба ( а в пространственной системе – и кручения ) могут рассматриваться как независимые; но продольные силы должны определяться из условий равновесия с учётом взаимодействия элементов в узлах; б) в случае температурного воздействия, вызывающего удлинения ( укорочения ) стержней, деформации элементов, как правило, взаимосвязаны и должны определяться исходя из совместности линейных перемещений узлов; в) взаимозависимыми являются также деформации элементов при кинематических воздействиях – смещениях связей, в т.ч. и дополнительно введённых в расчётные узлы. 20. Система канонических уравнений метода перемещений (СКУ МП). Смысл КУМП и их компонентов 1. Система канонических уравнений в целом по сути – статические условия эквивалентности основной системы МП и заданной системы при одинаковых воздействиях и истинных перемещениях Zрасчётных узлов; по форме – отрицание полных реакций всех дополнительных связей в расчётных узлах. 2. Произвольное ( i-е ) уравнение – отрицание полной реакции i-й введённой связи в ОСМП ( суммарной реакции Riот заданных воздействий ( ) и одновременных смещений всех введённых связей, равных истинным перемещениям Zрасчётных узлов ). 3. Левая часть i-го уравнения – полная реакция i-й введённой связи в ОСМП ( суммарная реакция Riот заданных воздействий ( ) и одновременных смещений всех введённых связей, равных истинным перемещениям Zрасчётных узлов ). 4. Свободный член i-го уравнения Ri – реакция i-й введённой связи в ОСМП от заданных воздействий ( ). 5. Слагаемое rikZki-го уравнения – реакция Riki-й введённой связи в ОСМП от смещения k- й связи, равного истинному перемещению Zk . 6. Коэффициент rikпринеизвестномZk в i-м уравнении – реакция i-й введенной связи в ОСМП от единичного смещения k- й связи Zk = 1 (единичная реакция). Собственные единичные реакции r11, r22 , …, rii, …, rnn введённых связей в ОСМП называются главными коэффициентами канонических уравнений МП, а величины 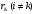 – побочными реакциями (побочными коэффициентами уравнений). – побочными реакциями (побочными коэффициентами уравнений).По теореме Рэлея о взаимности единичных реакций rik= rki . 21. Стандартные задачи для типовых элементов основной системы метода перемещений. Типовые элементы плоских стержневых ОСМП и стандартные задачи их расчёта Типовые стержневые элементы в общем случае различаются по – способам закрепления концов в узлах ( внутренних или опорных ) выбранной основной системы; – виду деформации ( изгиб, растяжение-сжатие, сложное сопротивление ); – закону изменения жёсткости ( при изгибе, растяжении-сжатии, кручении ) по длине стержня. В плоских стержневых ОСМП выделяют четыре основных типа элементов постоянного сечения ( рис. 1.19 ). Тип 1 Тип 2 EI = const EI = const Тип 3 Тип 4 EA = const EI = const Рис. 1.19 Для элементов 1-го и 2-го типов возможен учёт сдвига при поперечном изгибе ( при этом считается, что GA/ k = const ); для элементов 3-го и 4-го типа деформация сдвига в расчёте по методу перемещений не имеет значения. Элементы 1-го, 2-го и 4-го типов могут рассматриваться одновременно и как изгибаемые, и как продольно деформируемые с жёсткостью ЕА = const. Шарнир у элемента 2-го типа может располагаться на любом конце – левом или правом. В случае примыкания конца некоторого стержня к опорному узлу его защемление или шарнирное опирание может быть подвижным: или Если элемент 3-го типа абсолютно жёсткий ( 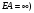 , то при отсутствии температурных воздействий стержень может рассматриваться как линейная связь. , то при отсутствии температурных воздействий стержень может рассматриваться как линейная связь.Стандартные задачи для типовых элементов ОСМП – определение реакций концевых связей ( усилий в концевых сечениях ) и внутренних силовых факторов ( эпюр M, Q, N) от следующих воздействий: 1) от смещений концевых связей (кинематических воздействий): а) поворота на угол защемлённого конца стержня ( для элементов 1-го и 2-го типов ); б) линейного смещения конца стержня относительно его противоположного конца: – по нормали к исходной ( недеформированной ) продольной оси; – в направлении исходной продольной оси; 2) от силовых воздействий – стандартных нагрузок ( произвольно расположенной одиночной сосредоточенной силы или сосредоточенного момента; нагрузки, распределённой по определенному закону, в частности, равномерной ); 3) от изменения температуры. Решения стандартных задач получаются методом сил или методом начальных параметров. 22. Свойства и способы определения коэффициентов при неизвестных и свободных членов СКУ МП. Коэффициенты ( единичные реакции 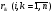 ) и свободные члены ( реакции введённых связей от заданных воздей- ) и свободные члены ( реакции введённых связей от заданных воздей-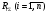 ) канонических уравнений МП могут определяться ) канонических уравнений МП могут определяться1) статическим методом – из условий равновесия узлов ( способ вырезания узлов ) или частей основной системы ( способ отсечения частей ); 2) кинематическим методом в двух вариантах: – через возможную работу концевых усилий и узловых нагрузок: 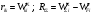 *); *);– способом «перемножения» эпюр: 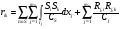 ; ( 1.16 ) ; ( 1.16 ), ( 1.17 ) 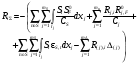 где 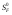 и и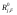 – внутренние силовые факторы и реакции упругих – внутренние силовые факторы и реакции упругихсвязей от заданной нагрузки ( силового воздейст- вия ) в любой статически определимой системе, полученной из рассчитываемой системы удале- нием лишних связей; S,t – свободные (нестеснённые) температурные дефор- мации, соответствующие силовым факторам S; (j) – компоненты заданных смещений связей; Si, Rj,i и R(j), i – внутренние усилия, реакции упругих и смещаемых связей в i - м единичном состоянии ( от Zi = 1 ) CS – жёсткость сечения стержня при деформации, соот- ветствующей усилию S; Cj – жёсткость j-й упругой связи. Для плоской стержневой системы: 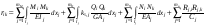 ; ( 1.18 ) ; ( 1.18 )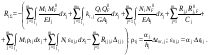 ( 1.19 ) ( 1.19 )Применение любого из указанных способов требует знания внутренних силовых факторов в элементах основной системы от различных воздействий – силовых, температурных ( заданных нагрузок и изменений температуры ) и кинематических ( заданных смещений связей, а также единичных смещений дополнительных связей в расчётных узлах ). Для этого служат результаты решения стандартных задач для типовых элементов ОСМП, которые даны в следующем параграфе. Вычисленные коэффициенты и свободные члены канонических уравнений должны быть проверены, для чего используется способ «перемножения» эпюр и суммарные единичные силовые факторы – внутренние усилия Ss от одновременных единичных смещений всех связей, введённых в расчётные узлы ( Z1 = 1, Z2 = 1, …, Zn = 1 ), реакции упругих связей Rj,s ( 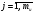 ) и реакции R(j),s связей с заданными смещениями (j) ( ) и реакции R(j),s связей с заданными смещениями (j) (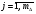 ): ):1) собственная обобщённая суммарная единичная реакция rss всех введённых связей, вычисляемая по формуле 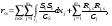 ( 1.20 ) ( 1.20 )должна быть равна сумме всех коэффициентов КУМП ( это универсальная проверка коэффициентов ): 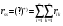 ; ( 1.21 ) ; ( 1.21 )2) суммарная единичная реакция i - й связи 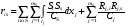 ( 1.22 ) ( 1.22 )должна быть равна сумме коэффициентов i- го канонического уравнения ( это построчная проверка коэффициентов, производимая при невыполнении условия ( 1.21 ) ): 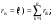 ( 1.23 ) ( 1.23 ) 3) обобщённая ( суммарная ) реакция Rs всех введённых связей от заданных воздействий, вычисляемая по формуле 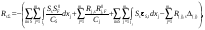 ( 1.24 ) ( 1.24 ) должна быть равна сумме всех свободных членов КУМП: 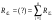 . ( 1.25 ) . ( 1.25 )Суммарные реакции ris,rss, Ri и Rs можно вычислять также через возможные работы концевых усилий и узловых нагрузок: 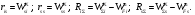 Дополнительными проверками коэффициентов, основанными на использовании свойств единичных реакций связей, могут служить а) контроль положительности собственных реакций rii ; б) сопоставление значений пар реакций rikи rki , вычисленных различными способами и приёмами ( статическими – из условий равновесия разных узлов или частей ОСМП, либо кинематическими ) – они должны удовлетворять условию взаимности rik = rki . 23. Определение внутренних усилий в заданной системе по найденным основным неизвестным метода перемещений. Промежуточные и окончательная проверки правильности решения. Решением системы канонических уравнений находятся основные неизвестные Z1 , Z2 , …, Zn, используемые затем для вычисления усилий S в ОСМП от этих смещений расчётных узлов вместе с заданными воздействиями. Если перемещения Z1 , Z2 , …, Zn найдены правильно, то усилия в ОСМП могут считаться равными ( с допустимыми вычислительными погрешностями ) искомым усилиям в заданной рассчитываемой системе. Согласно принципу суперпозиции воздействий, 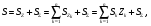 ( 1.26 ) ( 1.26 )где Sk – усилия в k - м единичном состоянии ОСМП ( от Zk = 1 ); S – усилия в ОСМП от заданных воздействий. Для элементов с преобладающим изгибом усилия S – это изгибающие моменты M и поперечные силы Q, для элементов типа затяжек, подкосов и т.п., а также для стержней ферм S – это продольные силы N. При выполнении расчёта «вручную» в первую очередь вычисляются изгибающие моменты 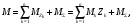 ( 1.27 ) ( 1.27 )затем – поперечные силы ( с помощью дифференциальной зависимости Q = dM/ dx и условий равновесия отдельных элементов ), после чего из уравнений равновесия узлов находятся продольные силы N. При необходимости, кроме силовых факторов в рассчитываемой системе, могут быть найдены и перемещения сечений любого элемента – для этого по найденным значениям перемещений Z расчётных узлов определяются компоненты смещений его концевых сечений, а затем одним из известных методов – Максвелла – Мора или начальных параметров – искомые перемещения сечений. Особенно просто эта задача решается для элемента постоянного сечения, уравнение изогнутой оси которого при равномерной нагрузке по всей длине есть полином четвёртой степени, а при отсутствии нагрузки – третьей степени. Полная проверка результатов расчёта деформируемой системы методом перемещений состоит из двух частей: 1) статическая проверка, заключающаяся в том, что при найденных значениях силовых факторов и заданных нагрузках выполняется контроль выполнения условий равновесия а) узлов, б) произвольно выделенных частей системы, в) системы в целом; В методе перемещений главной является статическая проверка, так как с её помощью контролируется выполнение исходного требования статической эквивалентности ОСМП и рассчитываемой системы ( см. стр. 20 ), а именно – обеспечения равновесия ОСМП при нулевых значениях реакций связей, введённых в расчётные узлы. Кинематическая проверка способна обнаружить ошибки а) обусловленные нарушениями совместности деформаций элементов и кинематических граничных условий в единичных состояниях ОСМП; б) вследствие несогласований деформаций элементов и усилий в них, допущенных при рассмотрении единичных состояний и учёте заданных воздействий. Заключается в вычислении, с использованием найденных значений усилий, перемещений по направлениям жёстких лишних связей в системе, полученной из заданной системы удалением этих связей ( как правило, одновременно всех, что даёт статически определимую основную систему метода сил*) ). Для выполнения этой проверки используются усилия в выбранной вспомогательной ОСМС от единичного основного неизвестного метода сил Xi = 1. Перемещение по направлению i - й удалённой лишней связи, которое должно быть равным нулю, определяется как 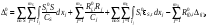 ( 1.28 ) ( 1.28 )где 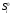 , ,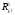 , ,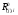 – соответственно внутренние усилия, реакции – соответственно внутренние усилия, реакцииупругих и смещаемых связей в ОСМС от Xi = 1; S и Rj – найденные расчётом по методу перемещений внутренние усилия и реакции упругих связей. Наряду с частными ( раздельными ) проверками 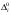 = 0 (?) ( i = = 0 (?) ( i = 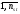 ) может выполняться универсальная кинематическая проверка ) может выполняться универсальная кинематическая проверка 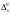 = 0 (?). Обобщённое перемещение по направлениям = 0 (?). Обобщённое перемещение по направлениямвсех удалённых лишних связей 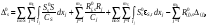 ( 1.29 ) ( 1.29 )где 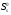 , ,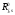 , ,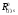 – суммарные единичные силовые факторы в – суммарные единичные силовые факторы вОСМС от одновременно приложенных всех основных неизвестных X1 = 1, X2 = 1, …, 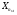 = 1. = 1. В общем случае деформации плоской системы при комбинированных воздействиях ( 1.30 ) 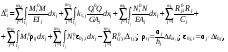 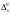 – аналогично ( 1.30 ), с заменой индекса « i» на « s». – аналогично ( 1.30 ), с заменой индекса « i» на « s». Замечание: при выполнении кинематической проверки должны учитываться те же виды деформаций элементов, что и при определении коэффициентов и свободных членов КУМП . 24. Учет деформаций растяжения-сжатия элементов в расчётах СНС методом перемещений. Необходимость учета продольных сил при расчете стержневых систем методом перемещений требует особого подхода к определению количества неизвестных в решаемых задачах. При этом формула (19.1) остается справедливой, т.е. по-прежнему 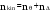 . .Число неизвестных угловых перемещений nθ остается таким же, как и в случае, когда влиянием продольных сил на конечный результат расчета мы пренебрегаем, т.е. оно равно количеству жестких узлов сооружения. В рассматриваемом случае иным становится число неизвестных линейных перемещений узлов системы nΔ, которое определяется по шарнирной схеме сооружения, образуемой теперь не только введением режущих цилиндрических шарниров в жесткие узлы, но и удалением тех элементов, где требуется учесть продольные силы. Пример 19.9.1. Определить степень кинематической неопределимости рамы, изображенной на рис. 19.27,а с учетом влияния продольных сил во всех стержнях и для ее расчета выбрать основную систему метода перемещений. Шарнирную схему рамы образуем введением во все жесткие узлы, включая и опорные, цилиндрических шарниров и удалением стержней 1А, 12, 2В (рис. 19.27,б). Степень свободы этой шарнирной схемы определим по формуле (19.2): W = 2Y − C − Co = 2 ∙ 4 − 0 − 4 = 4. 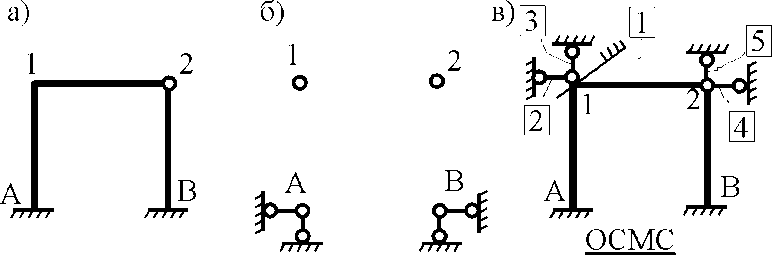 Рис. 19.27 Степень кинематической неопределимости рамы равна 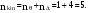 Основная система метода перемещений показана на рис. 19.27,в. Пример 19.9.2. Определить степень кинематической неопределимости комбинированной системы с учетом влияния продольных сил в стержнях 1А и 13 (рис. 19.28,а) и выбрать основную систему метода перемещений для ее расчета.  Рис. 19.28 Шарнирная схема заданной стержневой системы показана на рис. 19.28,б. Обращаем внимание, что при образовании этой шарнирной схемы стержни 1А и 13 удалены. Степень свободы шарнирной схемы W = 2Y − C − Co = 2 ∙ 6 − 5 − 5 = 2. Степень кинематической неопределимости рамы  Основная система метода перемещений изображена на рис. 19.28,в. Чаще всего продольные силы при расчетах сооружений учитываются в незагруженных элементах, имеющих на концах цилиндрические шарниры. Продольную силу в таких элементах от взаимного смещения их концов в направлении оси на величину, равную Δ определим методом сил (рис. 19.29,а).  Рис. 19.29 Основная система метода сил показана на рис. 19.29,б. Реакцию в удаленной связи определим из условия  (19.25) (19.25)Используя эпюру продольных сил от X1=1 (рис. 19.29,в,г), получим при ЕА=const:  Решив уравнение (19.25), имеем:  , ,где  – погонная жесткость стержня при его продольных деформациях. – погонная жесткость стержня при его продольных деформациях.Окончательную эпюру продольных сил определим с помощью соотношения N = N1 X1 (рис. 19.29,д). 25. Расчет симметричных СНС методом перемещений. Группировка неизвестных. Если в основной системе метода перемещений все эпюры внутренних усилий от единичных перемещений узлов (в том числе и групповых) имеют симметричный или обратно симметричный характер, то система канонических уравнений метода перемещений при произвольном внешнем воздействии (силовом, температурном или кинематическом) распадается на две независимых друг от друга системы уравнений, одна из которых содержит только симметричные неизвестные, а другая – только обратно симметричные |
