Матем қысқартылған. #1!Егер А(m x k), В(k x n) болса, онда Сав матрицасыны лшемі
 Скачать 457.63 Kb. Скачать 457.63 Kb.
|
|
*+кестелік, аналитикалық, графиктік #383*! 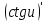 *+- #384*! *+ #385*! *+ #386*! *+ #387*!Берілген функция нүктеде дифференциалдануы үшін оның осы нүктеде ... болуы қажетті және жеткілікті. *+туындысы #388*! 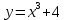 функциясының туындысы тең функциясының туындысы тең*+ 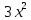 *10х #389*!(2х+3)dx өрнегі қандай функцияның дифференциалына сәйкес келеді *+ 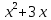 #390*! 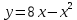 функциясының экстремумы қандай нүктеде бар болады функциясының экстремумы қандай нүктеде бар болады*+x=4 #391*! 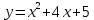 функциясының экстремумы қандай нүктеде бар болады функциясының экстремумы қандай нүктеде бар болады*+x=-2 #392*!sin(2x+3) функциясының туындысы тең *+2cos(2x+3) #393*! 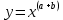 функциясының туындысы тең функциясының туындысы тең*+ 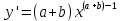 #39*! 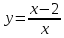 функциясының туындысы тең функциясының туындысы тең *+ 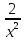 #39*!y=(x2+2x+2)e-xфункциясының туындысы тең *+-x2 e-x #396*!Егер 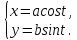 болса, онда болса, онда 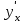 туындысы тең туындысы тең*+ 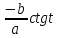 #397*!Егер 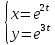 болса, онда болса, онда 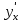 туындысы тең туындысы тең*+ 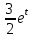 #398*!y = 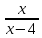 функциясы қандай нүктеде үзіліске ұшырайды және үзіліс нүктесінің тегі қандай функциясы қандай нүктеде үзіліске ұшырайды және үзіліс нүктесінің тегі қандай*+x = 4 - 2-ші текті үзіліс #399*! 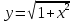 функциясының дифференциалы қай өрнекке сәйкес функциясының дифференциалы қай өрнекке сәйкес*+ 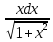 #400*!y=arcsin2x функциясының дифференциалы ... өрнегіне сәйкес *+ 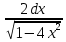 #401 *!2x-3y+1=0 айқындалмаған функциясының 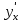 туындысы туындысы*+ 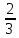 #402 *!x2+2xy+y2-3=0 айқындалмаған функциясының 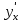 туындысы туындысы*+-1 #403 *!ех - еу = у – хайқындалмаған функциясының 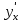 туындысы туындысы*+ 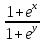 #404 *! 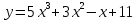 функциясының туындысы функциясының туындысы *+ 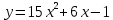 #405 *! 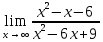 шегі тең шегі тең*+1 #406 *! 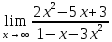 шегі тең шегі тең*+ 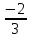 #407 *! 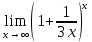 шегі тең шегі тең*+ 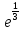 #408 *! 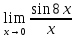 шегі тең шегі тең*+8 #409 *! 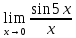 шегі тең шегі тең*+5 #410 *! 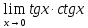 = шегі тең = шегі тең*+1 #411 *! 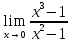 шегі тең шегі тең*+1 #412 *! 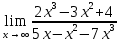 шегі тең шегі тең*+–2/7 #413 *! 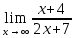 шегі тең шегі тең*+1/2 #414 *! 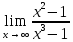 шегі тең шегі тең*+о #415 *! 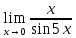 шегі тең шегі тең*+1/5 #416 *!а қандай мәнінде 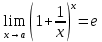 теңдігі дұрыс теңдігі дұрыс *+ 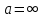 #417 *!а қандай мәнінде  теңдігі дұрыс теңдігі дұрыс*+ 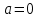 #418 *! 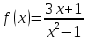 функциясының анықталу облысы функциясының анықталу облысы*+ 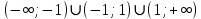 #419 *!Егер R=aQ+b функциясындағы Q мәніне 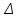 Q өсімшесін берсе, онда берілген функцияның өсімшесі Q өсімшесін берсе, онда берілген функцияның өсімшесі *+ 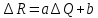 #420 *!Егер 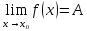 және және 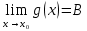 , онда , онда 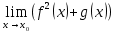 шегі тең шегі тең*+ 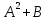 #421 *!Егер 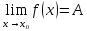 және және 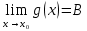 , онда , онда 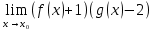 шегі тең шегі тең*+(А+1)(В-2) #422 *!Егер 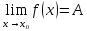 және және 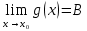 , онда , онда 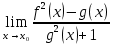 шегі тең шегі тең *+ 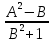 #423 *!Егер 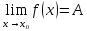 және және 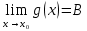 , онда , онда 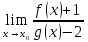 шегі тең шегі тең*+ 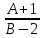 #434 *! 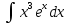 интегралындағы u және dv интегралындағы u және dv*+ 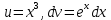 #435 *! 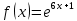 алғашқы функцияларының жиыны алғашқы функцияларының жиыны*+ 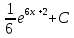 #436 *! *+тікелей интегралдау #437 *!Тікелей интегралдау әдісімен есептелетін интеграл *+  #438 *! 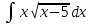 интегралы үшін интегралдау әдісі интегралы үшін интегралдау әдісі *+айнымалыны алмастыру әдісі #439 *! 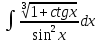 интегралы үшін интегралдау әдісі интегралы үшін интегралдау әдісі*+айнымалыны алмастыру әдісі #440 *! 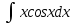 интегралы үшін интегралдау әдісі интегралы үшін интегралдау әдісі*+бөліктеп интегралдау әдісі #441 *!Айнымалыны алмастыру әдісімен есептелетін интеграл *+ 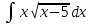 #442 *!Бөліктеп интегралдау әдісімен есептелетін интеграл *+ 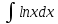 #443 *! 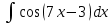 *+ 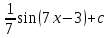 #444 *! 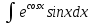 интегралдауда қолданылатын алмастыру интегралдауда қолданылатын алмастыру*+t=cosx #445 *! 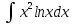 интегралындағы u және dv интегралындағы u және dv *+  #446 *! 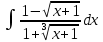 интегралындағы алмастыру интегралындағы алмастыру*+ 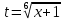 #447 *! 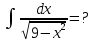 *+ 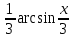 #448 *! 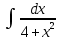 *+ 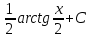 * 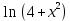 #449 *! 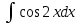 *+ 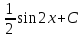 #450 *! 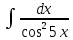 *+ 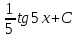 #451 *! 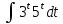 *+ 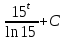 #452 *! 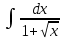 интегралын есептеу үшін қолданылатын алмастыру интегралын есептеу үшін қолданылатын алмастыру*+x=t2 #453 *! 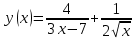 функциясы үшін алғашқы функция функциясы үшін алғашқы функция*+ 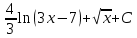 #454 *! 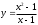 функциясын үзіліссіздікке зерттеңіз функциясын үзіліссіздікке зерттеңіз*+x=1 – бірінші текті үзіліс нүктесі #462 *! 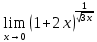 *+ 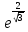 #464 *! 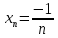 тізбегінің алғашқы үш мүшесі тізбегінің алғашқы үш мүшесі *+ 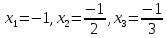 #465 *! 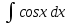 ? интегралы үшін интегралдау әдісі ? интегралы үшін интегралдау әдісі*+тікелей интегралдау #466 *! 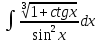 интегралы үшін интегралдау әдісі интегралы үшін интегралдау әдісі*+айнымалыны алмастыру әдісі #467 *!Берілген функциялардың қайсысы периодты *+y=sin2x #468 *!«Алынбайтын» интегралдар *+ 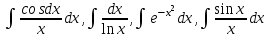 #469 *! *+ #470 *! 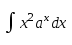 интегралындағы u және dv интегралындағы u және dv*+ 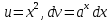 #471 *! *+t=cosx #472 *! *+ #473 *! 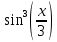 функциясының туындысы функциясының туындысы*+ 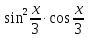 #474 *!y=5x5функциясының үшінші ретті туындысы *+300 x2 #475 *!y=eax функциясының екінші ретті туындысы *+a2eax #476 *!(2х-5)dx өрнегі ... функциясыныңдифференциалына сәйкес *+ 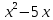 #477 *!y=2x3-5x2+7x+4 функциясының туындысы тең *+6x2-10x+7 #478 *! 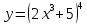 функциясының туындысы тең функциясының туындысы тең *+ 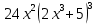 #479 *!y=tglnx функциясының туындысы тең *+ 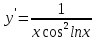 #480 *! 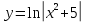 функциясының туындысы тең функциясының туындысы тең*+ 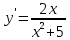 #481 *!y=4x3 функциясының екінші ретті туындысы тең *+12x2 #482 *!f(х)=x2-5x+4 функциясының 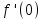 туындысы тең туындысы тең*+-5 #483 *!y=sin3x функциясының туындысы *+3sin2xcosx #484 *!y=2cosx функциясының туындысы *+- 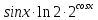 #485 *!y=lncos3x функциясының туындысы *+–3tg3x #486 *!y=arctg2x функциясының туындысы *+ 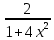 #487 *! 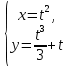 болса, онда болса, онда 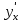 туындысы туындысы*+ 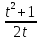 * 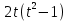 #488 *!y=(2x-3)3 функциясының екінші ретті дифференциалы қай өрнекке сәйкес *+24(2x-3) dx2 #489 *!у=х2-4х-1функциясының өсу аралығы *+(2,  ) )*(-  ,-2) ,-2)#490 *!у=х3+3х2-5 функциясының минимум нүктесі х тең *+о #491 *!у=х3+3х2-5 функциясының максимум нүктесі хтең *+-2 #492 *!у=х2-4х-1функциясының кему аралығы *+(-  ,2) ,2)#493 *!у = 3х-х3 функциясының [-2;0] кесіндісіндегі ең үлкен мәні *+у(-2)=2 #494 *!у =3х-х3 функциясының [-2;0] кесіндісіндегі ең кіші мәні *+у(-1)=-2 #495 *!у=х3-3х2+1 функциясының иілу нүктесі *иілу нүктесі жоқ *+x=1 #496 *!у= 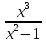 функциясы графигінің тік асимптотасы функциясы графигінің тік асимптотасы *+х= 1 #497 *!у = 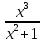 қисығының көлбеу асимптотасы қисығының көлбеу асимптотасы *+у=х #498 *!у = 9х2-9х3қисығының иілу нүктесі *+х= 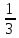 #499 *!у=х3-3х2+1функциясы графигінің ойыс болу аралығы *+(-  ,1) ,1) #500 *! 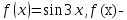 *+-9sin3x #501 *! 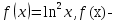 *+ 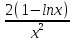 #502 *! 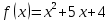 функциясының функциясының 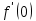 нүктесіндегі туындысы тең нүктесіндегі туындысы тең*+5 #503 *! 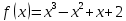 функциясының функциясының 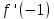 нүктедегі туындысы тең нүктедегі туындысы тең*+6 #504 *! 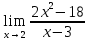 *+10 #505 *! 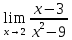 *+ 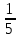 #506 *! 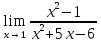 *+ 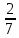 #507 *! 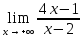 *+4 #508 *! 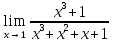 *+ 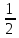 #509 *! 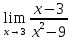 *+ 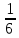 #510 *! 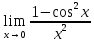 *+ 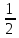 #511 *! 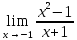 *+-2 #512 *! 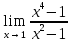 *+2 #513 *! 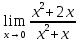 *+2 #514 *! 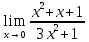 *+1 #515 *! 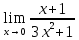 *+1 #516 *! 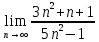 тізбегінің шегі тізбегінің шегі *+3/5 #517 *!  тізбегінің шегі тізбегінің шегі*+  #518 *!  тізбегінің шегі тізбегінің шегі*+10 #519 *!  тізбегінің шегі тізбегінің шегі*+-1 #520 *!  тізбегінің шегі тізбегінің шегі*+o #521 *!  *+9 #522 *!  *+6 #523 *!  *+ #524 *!  *+ 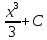 #525 *! 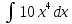 *+ 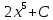 #526 *! 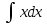 *+ 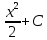 #527 *! 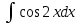 *+ 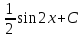 #528 *! 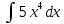 *+  #529 *!  *+  #530 *!  *+ 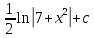 #531 *! 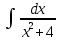 *+ 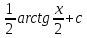 #532 *! 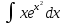 *+ 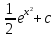 #533 *! 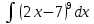 *+ 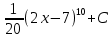 #534 *! 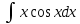 *+xsinx+cosx+c #535 *!  *+ln|lnx|+c #536 *!  *+  #537 *!  *+ 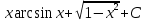 #538 *! 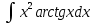 *+ 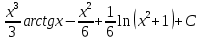 #539 *!  *+  #540 *! 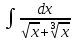 *+ 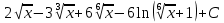 #1 *!Егер функция f(x) жұп болса, онда 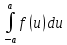 = =*+ 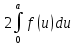 #2 *!Егерf(x)функциясының таңбасы [a, b] кесіндісінде ақырлы сан рет өзгерсе, онда y=f(x),Оx, x=a, x=b сызықтарымен шектелген жазық фигураның ауданы тең *+  #3 *!Анықталған интегралдың жазылутүрі *+  #4 *!Анықталған интегралда алмастыру әдісінің формуласы *+ #5 *!Анықталған интегралда бөліктеп интегралдау әдісінің формуласы *+ #6 *!Анықталған интегралда функцияның алгебралық қосындысы *+ 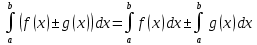 #7 *!Анықталған интегралдың шектерін алмастырғанда интегралдың таңбасы ... өзгереді *+қарама-қарсыға #8 *!Егер функция [a,b], [a,c], [c,b] кесінділерінің ең үлкенінде интегралданатын болса, онда *+ 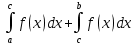 #9 *!Егер интегралдау шектері бірдей болса, онда *+ 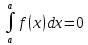 #10 *!Ньютон-Лейбниц формуласы *+ #11 *! 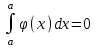 теңдігі нені білдіреді? теңдігі нені білдіреді?*+егер интегралдың шектері бірдей болса, онда анықталған интеграл нөлге тең #12 *! 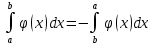 теңдігі нені білдіреді? теңдігі нені білдіреді?*+егер интегралдың шектерін ауыстырса, онда оның таңбасы қарама-қарсыға ауысады #13 *!  теңдігі нені білдіреді? теңдігі нені білдіреді?*+алгебралық қосындының интегралы оның әрбір мүшесінің интегралдарының қосындысына тең #14 *!  теңдеуі арқылы берілген қисықтың доғасының ұзындығының формуласы теңдеуі арқылы берілген қисықтың доғасының ұзындығының формуласы*+  #15 *!  қисық сызықты трапециясынОх осінің айналасындаайналдыру арқылы алынған дененің көлемі қисық сызықты трапециясынОх осінің айналасындаайналдыру арқылы алынған дененің көлемі*+ 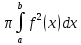 #16 *! 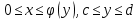 қисық сызықты трапециясынОу осінің айналасында айналдыру арқылы алынған дененің көлемі қисық сызықты трапециясынОу осінің айналасында айналдыру арқылы алынған дененің көлемі*+ 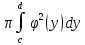 #17 *! 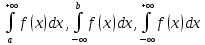 түрінде берілген интегралдың аталуы түрінде берілген интегралдың аталуы*+меншіксіз интеграл #18 *! 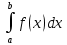 түрінде берілген интегралда а-ның аталуы түрінде берілген интегралда а-ның аталуы*+интегралдың төменгі шегі #19 *! 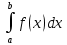 түрінде берілген интегралда в-ның аталуы түрінде берілген интегралда в-ның аталуы*+интегралдың жоғарғы шегі #20 *! 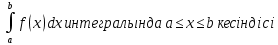 ... аталады ... аталады*+интегралдау кесіндісі *!Егер a≤x≤b кесіндісінде интегралданатын f(x) функциясы теріс емес болса, онда 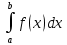 анықталған интегралы...aABb қисық сызықты трапецияның ауданына тең анықталған интегралы...aABb қисық сызықты трапецияның ауданына тең*+y=f(x)функциясының графигімен,Ох осімен және x=a, x=b түзулерімен шектелген #22 *!Егер 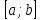 аралығында М – ең үлкен, m – ең кіші f(x)болса, онда аралығында М – ең үлкен, m – ең кіші f(x)болса, онда *+ 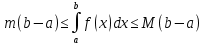 #23 *! 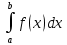 орта мәні жөніндегі теорема орта мәні жөніндегі теорема*+ 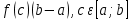 #24 *! *+f(x)-f(a) #25 *!Төменгі жағынан  функциясының графигімен, жоғарғы жағынан функциясының графигімен, жоғарғы жағынан  функциясының графигімен және x=a, x=b, aтүзулерімен шектелген фигураның ауданынесептеу формуласы: функциясының графигімен және x=a, x=b, aтүзулерімен шектелген фигураның ауданынесептеу формуласы:*+  #26 *!Егер f(x)функциясы  интегралы деп ... аталады интегралы деп ... аталады*+ 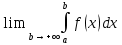 #27 *! 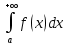 меншіксіз интегралы жинақты болады, егер меншіксіз интегралы жинақты болады, егер*+ 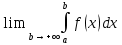 шегі бар және ақырлы шегі бар және ақырлы#28 *! 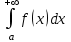 меншіксіз интегралы жинақсыз, егер меншіксіз интегралы жинақсыз, егер*+ 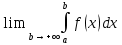 ақырсыз ақырсыз #29 *! 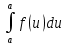 = =*+o #30 *! Егер 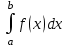 анықталған интегралы бар болса, онда анықталған интегралы бар болса, онда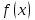 функциясы функциясы *+[a,b] аралықта интегралданады #31 *! 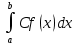 =? =?*+ 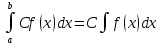 #32 *!Анықталған интегралды интегралдық қосындының шегі ретінде қарастырғанда интеграл таңбасының астындағы функция болу керек: *+[a,b] шектелген #1*! *+ 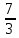 #2*! *+2 #3*! *+18 #4*! *+1 #5*! *+1 #6*! *+15 #7*! *+ 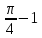 #8*! *+0,25 #9*! *+1 #10*! *+  #11*! *+  #12*! *+2 #13*! *+ 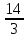 #14*! *+0,5 #15*! *+ 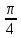 #16*!Егер *+5 #17*! 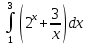 = =*+ 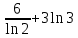 #1*! 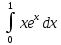 = =*+1 #2*! 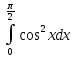 = =*+ 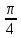 #3*! 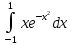 = =*+о #4*! 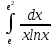 = =*+ 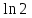 #5*!  сызықтарымен шектелген фигураның ауданы сызықтарымен шектелген фигураның ауданы*+  #6* 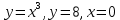 сызықтарымен шектелген фигураның ауданы сызықтарымен шектелген фигураның ауданы*+12 #7*!у=х, у=2х, х=2 сызықтарымен шектелген фигураның ауданы *+2 #8*! y=x3, x=1, y=0 сызықтарымен шектелген Ох осі бойымен айналған дененің көлемі *+ 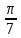 #9*! y=x3, y=1, x=0 сызықтарымен шектелген Oy осі бойымен айналған дененің көлемі *+ 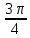 #10*! 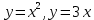 сызықтарымен шектелген фигураның ауданы сызықтарымен шектелген фигураның ауданы*+4,5 #11*! 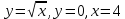 сызықтарымен шектелген фигураның ауданы сызықтарымен шектелген фигураның ауданы*+ 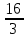 #12* 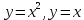 сызықтарымен шектелген фигураның ауданы сызықтарымен шектелген фигураның ауданы*+ 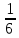 #13*!y=sinx қисықтың доғасымен және 0x осьімен (0; 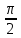 ) шектелген аудан ) шектелген аудан *+1 #14 *! xy=4 гипербола және x=2, x=3, y=0 түзулерімен шектелген қисықсызықты трапецияның ауданы *+4ln1,5 #15*! 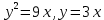 сызықтарымен шектелген Oy осі бойымен айналған дененің көлемі сызықтарымен шектелген Oy осі бойымен айналған дененің көлемі *+ 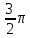 #16*! 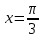 –тен –тен 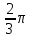 дейінгі y=lnsinx қисық доғасының ұзындығы дейінгі y=lnsinx қисық доғасының ұзындығы*+ 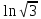 #17*! 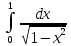 = =*+ 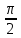 #18*! 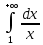 = =*++∞ #19*! 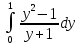 = =*+-0,5 #20*! 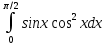 = =*+ 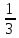 #21*! 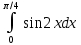 = =*+ 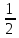 #22*! 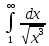 = =*+2 #23*!а қандай мәнінде у=х³, у=0, х=а, а>0 қисықтарымен шектелген фигураның ауданы 64 тең? *+4 #24*!у=х-х², у=х²-х сызықтарымен шектелген фигураның ауданы *+ 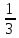 #25*! 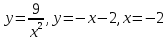 сызықтарымен шектелген фигураның ауданы сызықтарымен шектелген фигураның ауданы*+1 #26 *! 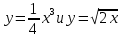 сызықтарымен шектелген фигураның ауданы сызықтарымен шектелген фигураның ауданы*+ 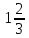 #27 *!а қандай мәнінде 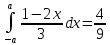 теңдігі орындалады? теңдігі орындалады?*+  |
