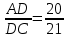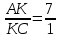Задачи на т. Пифагора. 2. 1 Применение теоремы Пифагора при решении задач курса планиметрии

• Название: 2. 1 Применение теоремы Пифагора при решении задач курса планиметрии
• Дата: 03.01.2023
• Размер: 57.57 Kb.
• Имя файла: Задачи на т. Пифагора.docx
• Тип: Задача; #871787

2.1 Применение теоремы Пифагора при решении задач курса планиметрии

Теорема Пифагора является одной из самых частых теорем, применяемых на применяемых на практике при решении задач. Она является основополагающей теоремой школьного курса геометрии, так как на данную теореме строится дальнейшее изучение геометрии, поэтому ее часто можно встретить при решении олимпиадных задач, а также в тестах ОГЭ и ЕГЭ.

В данной курсовой работе будут приведены как простые задачи на применение теоремы Пифагора, так и более сложного уровня, а также задачи, которые встречаются в КИМах ЕГЭ и ОГЭ.

Задача 1. В треугольнике ABC к стороне AC проведена высота BD. Сторона AB = 20, AD=16, DC = 9. Найти сторону BC [10].

Дано: △ABC, BD⏊AC. AB = 20. AD = 16. DC = 9. Найти: BC -?

Решение:

1) BD⏊AC (по условию) △ABD и △DBC – прямоугольные.

2) По теореме Пифагора BD² + AD² = AB².

BD² = AB² - AD².

3) По теореме Пифагора BC² = BD² + DC².

BC² = (AB² - AD²) + DC².

BC = = 15.

Ответ: BC = 15.

Задача 2. В треугольнике ABC один из углов при основании равен 45⁰, а высота BD делит основание на части 20 и 21. Найдите большую боковую сторону [10].

Дано: ABC BDAC BAC=45, Найти: большую боковую сторону

Решение:

1) Рассмотрим △ABD: A = 45⁰ (по условию), D = 90⁰ (так как BD⏊AC) ABD = 45⁰ и △ABD – равнобедренный AD = BD = 20, а DC = 21.

2) По теореме Пифагора: AB = = = .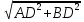

BC = 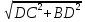= = 29.

3) Большая боковая сторона 29.

4) Если предположить, что стороны делятся иначе AD = 21, DC = 20, то по аналогичному решению получим: AB = 21 , BC = 29.

5) Большая боковая сторона 21 .

Ответ: 29 или 21 .

Задача 3. ABCD – равнобедренная трапеция, где боковые стороны равны 13, а верхнее основаниеравно 10. AK и BE – высоты трапеции. Площадь трапеции ABCD [10].

Дано: ABCD – равнобедренная трапеция. AD = BC = 13 AB = 10 AK⏊DC, BE⏊DC Найти: SABCD - ?

Решение:

1) DK = CE (△ADK = △CBEпо гипотенузе и острому углу).

2) ABEK – прямоугольник, тогда KE = 10, а DK = 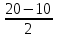= 5.

3) △ADK – прямоугольный  по теореме Пифагора: AK = 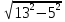= 12.

4) S_ABCD = AK(AB+CD) = 180.

Ответ: S_ABCD = 180.

Задача 4. AKMN – ромб, в котором диагонали AM = 10, KN = 24. Найдите длину стороны AK и площадь ромба AKMN [10].

Дано: AKMN – ромб AM = 10 KN = 24 Найти: AK - ? SAKMN - ?

Решение:

1) KO = ON = 12.

2) AO = OM = 5.

3) △AKO - прямоугольный. По теореме Пифагора: AK² = KO² + AO²;

AK = 13.

4) S_AKMN = (KN⋅AM) = 120.

Ответ: AK = 13, S_AKMN = 120.

Задача 5. В треугольнике ABC угол BAC прямой, длины сторон AB и BC равны соответственно 1 и 3. Точка K делит сторону AC в отношении 7:1, считая от точки A. Что больше: длина AC или длина BK [написана самостоятельно]?

Дано: ABC BAC=90 AB =1, BC =3, Что больше: длина AC или длина BK?

Решение.

1) Чтобы найти BK, которая является биссектрисой в ABK, нужно знать длину катета AK. Найдем его:



2) Теперь для треугольника ABK составим теорему Пифагора: BK²=AB²+AK²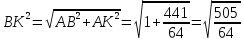



3) Сравним числа   и 3.

Для этого представим 3 как 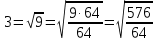, таким образом  длина AC больше

Ответ: длина AC больше.

Задача 6. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки, равные 5 и 12. Найдите катеты треугольника [написана самостоятельно].

Дано: ABC С=90 (O;r) – вписана в ABC (O;r)AB=M BM=15, MA=5 Найти: AC и CB

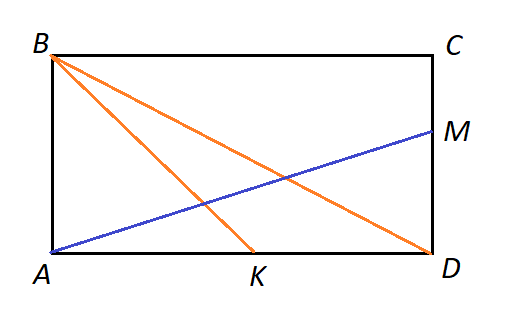
Решение. По свойству касательных, проведенных к окружности из одной точки, имеем: BM=BN=12, AM=AK=5, CK=CN=x. Тогда

AC²+BC²=AB²

(5+x)²+(12+x)²=17²

x²+17x-60=0  

По теореме Виета получаем корни: 3 и (-20). По условию устраивает положительный корень. Катеты равны тогда 8 и 15.

Ответ: 8 и 15.

Задача 7. В прямоугольнике ABCD длины отрезков AB и BD равны соответственно 2 и 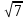 . Точка M делит отрезок CD в отношении 1:2, считая от точки C, K – середина AD. Что больше: длина BK или длина AM [написана самостоятельно]?

Дано: ABCD – прямоугольник AB=2, BD= AK=KD Что больше: длина BK или длина AM

Решение.

1. 
   Определим сначала BK. Для этого найдем AK.
   

AB²+AD² = BD²

AD²=BD² - AB²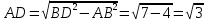



  

2. 
   Рассмотрим ABK, где BR – гипотенуза.
   

BK²=AB²+AK²

3. 
   Найдем теперь AM: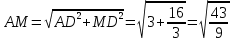
   

  

4. 
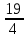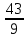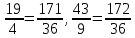   Осталось сравнить дроби   и  . При приведении к общему знаменателю получаем ,  длина AM больше длины BK.
   

Ответ. Длина AM больше длины BK.

Задача 8. Задача арабского математика XI в. На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба [15]?

Решение:

В АDВ: АВ² =ВD² +АD², АВ²=30² +Х², АВ²=900+Х²

В АЕС: АС²= СЕ²+АЕ², АС²=20²+(50 – Х)², АС²=400+2500 – 100Х+Х², АС²=2900 – 100Х+Х².

Но АВ=АС, так как обе птицы пролетели эти расстояния за одинаковое время. Поэтому АВ² =АС²,900+Х² =2900 – 100Х+Х²,100Х=2000,Х=20, АD=20.

Значит, рыба была на расстоянии 20 локтей от большой пальмы.

Ответ: 20 локтей.