Епггппг. Документ Microsoft Word (3). 2. гидравлика

• Название: 2. гидравлика
• Анкор: Епггппг
• Дата: 12.11.2022
• Размер: 272.5 Kb.
• Имя файла: Документ Microsoft Word (3).doc
• Тип: Закон; #783940

2. ГИДРАВЛИКА

2.1 ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ
Жидкость. Изучение основных законов механики жидкости (газов) необходимо начинать с особенностей различия свойств жидкостей и твердых тел.

Жидкость отличаются от твердых тел отсутсвием «твердой кристаллической решетки» и значительной свободой подвижности молекул. Изменение принятой формы жидкости происходит под действием даже при приложении самых малых сил (например, жидкость течет под действием собственного веса).

Жидкость имеет молекулярное строение - состоит из молекул, т.е. жидкость, имеет прерывистую структуру. В механики жидкости для простоты решения большинства задач принимают жидкость как сплошную (непрерывную) среду. Таким образом, вместо реальной физической субстанции самой жидкости изучается ее модель, обладающая свойством непрерывности (гипотетически сплошная среда). Введение аксиомы о непрерывности упрощает создание математического аппарата, описывающего состояния жидкости.

По своим физическим свойствам жидкость можно условно разделять на два состояния мало сжимаемые (капельные) и сжимаемые (газообразные).

Капельные жидкости обладают определенным объемом, который, например, изменяется под действием определенных сил. Газы, занимают все пространство и могут значительно изменять объем, сжимаясь и расширяясь под воздействием определенных сил.

Плотность жидкости. Плотностью жидкости , называется масса М, заключенная в единице объема W:
(1)
Например, плотность воды при температуре 4° С .

Удельный вес. Вес жидкости G, приходящийся на единицу объема W называется удельным вес
(2)
Удельный вес воды при температуре 4°С .

Плотность и удельный вес жидкости связаны между собой соотношением
(3)
где g — ускорение свободного падения.

Сжимаемость жидкостей. Сжимаемость капельных жидкостей под действием давления характеризуется коэффициентом объемного сжатия , который представляет собой относительное изменение объема жидкости на единицу изменения давления:
(4)
где W—первоначальный объем жидкости; dW—изменение этого объема при увеличении давления на величину dр.

Коэффициент объемного сжатия имеет размерность Па^-1. Знак «минус» в формуле (4) обусловлен тем, что положительному приращению давления соответствует отрицательное приращение (т. е. уменьшение) объема жидкости W. Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкости Е₀, Па:
(5)
Температурное расширение жидкостей. Температурное расширение капельных жидкостей характеризуется коэффициентом температурного расширения , выражающим относительное увеличение объема жидкости при увеличении температуры на 1 град, т. е.
, (6)
где dW—изменение этого объема при повышении температуры на величину dt.

Газы характеризуются значительной сжимаемостью и высокими значениями коэффициента температурного расширения. Зависимость плотности газов от давления и температуры устанавливается уравнением состояния.

Наиболее простыми свойствами обладает газ, разрешенный настолько, что взаимодействие между его молекулами может не учитываться, так называемый идеальный газ. Для идеальных газов справедливо уравнение ’’Клайперона’’, позволяющее определять плотность газа при известных значениях давления и температуры:
, (7)
где р—абсолютное давление, R—удельная газовая постоянная, различная для разных газов, но не зависящая от температуры и давления [для воздуха R = 287 Дж/(кг·К)]; Т—абсолютная температура.

Поведение реальных газов в условиях, далеких от сжижения, незначительно отличается от поведения идеальных газов.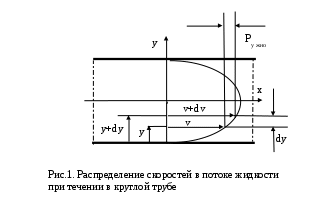



Вязкость жидкостей. Вязкостью называется свойство жидкостей оказывать сопротивление сдвигу. Все реальные жидкости обладают определенной вязкостью, которая проявляется в виде внутреннего трения при относительном перемещении смежных частиц жидкости.

Если рассматривать течение жидкости параллельными слоями (рис. 1) то можно предположить зависимость между напряжением деформацией в виде:
(8)
Величина называется коэффициентом динамической вязкости.

Сила внутреннего трения в жидкости может быть определена из выражения
, (9)
где площадь трения.

Трение в жидкости отличается от трения в твердых телах, где сила трения зависит от нормального давления и не зависит от площади трущихся поверхностей.

Вязкость жидкостей в большой степени зависит от температуры, при этом вязкость капельных жидкостей при увеличении температуры уменьшается, а вязкость газов возрастает.

В гидравлике находит применение понятие кинематической вязкости v, представляющей собой отношение динамической вязкости жидкости к ее плотности:
(10)
Эта вязкость названа кинематической, так как в ее размерности отсутствуют единицы силы или массы.

Аномальные жидкости. В природе, кроме обычных, так называемых “Ньютоновских жидкостей” существуют аномальные “Неньютоновские жидкости”. К этим жидкостям относятся некоторые смазочные масла, краски, суспензии, коллоидные растворы, жидкие полимеры. К числу аномальных жидкостей относятся также феррожидкости, ферромагнитные, электрореологические, переохлажденные (жидкости типа смол). Как правило, такие жидкости в определенных условиях имеют упругие деформации, а в других условиях вязкие деформации при течение.
добавить

2.2 ОСНОВЫ ГИДРОСТАТИКИ

2.2.1 РАВНОВЕСИЕ ЖИДКОСТИ

Действующие силы и равновесное состояние жидкости. Рассмотрим некоторый объем жидкости рис.2.2.1

Рассматриваемый объем жидкости находится в состоянии относительного равновесия. В этом случае выделенная точка М также находится в состоянии равновесия. Такое состояние предполагает равновесное состояние сил, воздействующих на выделенный объем.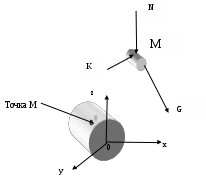



Рис. 2.2.1.
На выделенный объем действуют внешние силы – поверхностные и объемные силы. Объемные силы – это внешние силы пропорциональные объему и плотности вещества. Поверхностные силы – силы, действующие в границах выделенного объема. Условие равновесия предполагает присутствие нормальной составляющей N и касательной составляющей K. Касательная составляющая К для условия относительного равновесия должна бать равна нулю. Таким образом, условие относительного равновесия в рассматриваемом случае предполагает равенство поверхностных и объемных сил.

Поверхностные силы. Поверхностные силы определяют так называемое поверхностное «напряжение». Поверхностное напряжение определяется выражением:
, (11)
где Р - действующая поверхностная сила, - площадь взаимодействия поверхностной силы.

Объемные силы. Объемные силы (массовые силы) определяются воздействие внешних сил. Для них можно записать:

(12)
Основная теорема гидростатики. Основная теорема гидростатики устанавливает то, что гидростатическое давление (р) в данной точке не зависит от его направления, т.е.:

, (13)

.где давления по направлению осей координат x,y,z и произвольному направлению i.

Рассмотрим некоторый элементарный объем жидкости (рис.2.2.2.) при условии, что он находится в состоянии равновесия.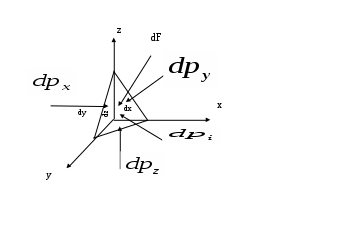


Рис. 2.2.2.
В этом случае можно состояние равновесия выразить в виде трех уравнений проекций действующих сил и трех уравнений моментов:
и
и
и

(14)
При уменьшении граней выделенного объема в пределе до нуля система действующих сил превратится в систему сил, проходящих через точку, а система уравнений моментов теряет смысл.

Проекции этих сил на оси x, y, z можно представить в виде:




,

(15)

Где угол между нормальным направлением силы и соответствующей осью координат, а углы между составляющей равнодействующих массовых сил и осями координат.
Учитывая, что
;

и .
Проводя подобные рассуждения, относительно проекций сил на другие оси координат, и осуществляя соответствующие преобразования, получим:
-
-
(16)


Или, проведя соответствующие преобразования окончательно, получим:



(17)

Учитывая, что последняя составляющая в данной системе уравнений, представляет величину высшего порядка малости, можем записать:



(18)

или


Что и требовалось доказать.

В данном случае было доказано равнозначность гидростатического давления в точке по любому направлению, однако не следует забывать, что давление является функцией координат и времени.



Основной закон гидростатики. Выделим в объеме некоторую элементарную площадку 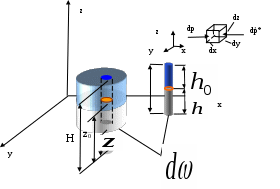. Данная площадка сверху нагружена столбом жидкости высотою , где высота столба жидкости (воздуха) над свободной поверхностью жидкости.



Р ис.2.2.3.
Предполагая, что жидкость находится в состоянии относительного покоя. Выделим элементарный объем рис.2.2.3.

Условие равновесия выделенного элементарного объема предполагает равенство массовых и поверхностных сил. В проекциях на оси x, y, z можем записать:

(19)

или


(19 а)

Система уравнений (19 а) описывает относительное равновесное состояние жидкости (система уравнений равновесного состояния жидкости-Эйлера).

Сложение правых и левых частей уравнения позволяет получить уравнение:
(20)
Уравнение (20) представляет собой основное уравнение гидростатики.

Уравнение поверхности уровня. Поверхность уровня представляет поверхность равного давления. Поверхность уровня предполагает или

В этом случае уравнении (20) примет вид:
(21)
Уравнение (21) представляет уравнение поверхности уровня.

Поверхность уровня обладает определенными свойствами:

1. 
   Поверхности уровня не пересекаются.
   
2. 
   Направление объемных сил нормально к поверхности уровня.
   

Равновесие жидкости в поле земного тяготения. Рассматривая уравнение (20) для случая работы его в поле земного тяготения, т.е. X=0, Y=0, а Z=-g (см. рис. 2.2.3). В данном случае уравнение (20) примет вид
(22)
Проводя интегрирование уравнения (22) окончательно получим
(23)
Где величина гидростатического давления столба воздуха над выделенной поверхностью; -высота столба воздуха; - высота столба жидкости над выделенной поверхности.

Окончательно уравнение (23) примет вид: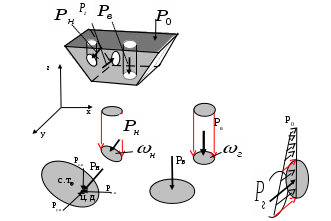
(23 а)

Рис. 2.2.3
Сила давления жидкости на плоские поверхности. Определим силу давления P_н на произвольную наклонную площадь (рис.2.2.3). В данном случае величина P_н определяется из соотношения:
, (24)
Проекции силы P_н на оси xyz можно определить из выражений:


(25)



Где углы пространственной ориентации силы P_н

и осей координат xyz.

Центр давления. Центром давления называется точка приложения силы давления в столбе жидкости на расчетную площадку. Центр давления характеризуется координатами xyz, а для плоскости двумя координатами. В этом случае положение центра давления можно определить из выражения
, (26)
Где расстояние от поверхности уровня жидкости до точки приложения силы давления;

момент инерции площадки относительно рассматриваемой оси, проходящей через центр тяжести площадки;

расстояние от поверхности уровня жидкости до центра тяжести площадки;

угол ориентации площадки .

Для рассматриваемого случая, величина, т.е. центр давления всегда ниже центра тяжести рассматриваемой площадки. Исключение составляет частный случай, когда площадка, расположена горизонтально, в плоскости xoy. В этом случае центр давления совпадает с центром тяжести площадки. Расстояние между центром тяжести и центром давления принимается как эксцентриситетом приложения силы давления и центром тяжести.

Давление жидкости на криволинейные поверхности. Рассмотрим криволинейную поверхность (рис.2.2.4).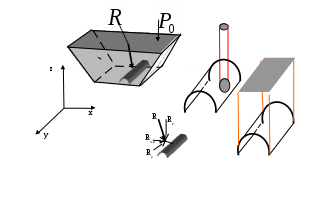




Рис. 2.2.4

Так как поверхность пластины криволинейная, то силы dR образуют систему не параллельных сил. Такую систему можно привести к главному вектору R. В общем случае можем записать:


(27)

,

где углы пространственной ориентации силы R

и осей координат x y z.

Сумма проекций элементарных сил может быть выражена в виде равнодействующей силы R;


(28)

,

Сила R по величине будет рана;

, (29)
Решение уравнений (28) можно представить в виде:



(30)

,

где - глубина погружения центра тяжести площадок, соответственно .
Закон Архимеда. Погрузим тело произвольной формы (рис. 2.2.5) в жидкость. Определим величину сил воздействующих на рассматриваемое тело. На рассматриваемое тело действуют поверхностные и массовые силы. Проекции рассматриваемых сил приведены на рис. 2.2.5.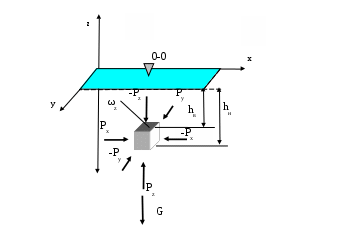


Рис.2.2.5
P_x, P_y, P_z –проекции поверхностных сил соответственно на оси координат x,y,z. Учитывая, что данная система находится поле сил земного тяготения, массовая сила, действующая на погруженное тело, составит
G=γ_т×ω_z ×(h_н-h_в), (31)
где h_н и h_в глубина погружения нижней и верхней граней тела, γ_т=ρg удельный вес погруженного тела, площадь грани нормальной к оси z.

В случае нахождения рассматриваемого тела в состоянии равновесия сумма поверхностных и массовых сил должна быть равна нулю.
, (32)
где G – сумма проекций массовых сил, R- сумма проекций поверхностных сил.

Подставляя в уравнение (32) составляющие получим
-γ_т×ω_z×(h_н-h_в)+γ_в×ω_z×(h_н­h_в)=0 (33)
или
-γ_т×W_т+ γ_в×W_в=0 (34)
Из анализа уравнения (34) следует, что в случае равенства удельного веса тела и воды тело находится в состоянии покоя. При условии γ_в >γ_т тело должно всплыть, а при условии γ_в<γ_т тело опустится на дно емкости.


2.3. ОСНОВЫ ГИДРОДИНАМИКИ
2.3.1 Основные характеристики потока жидкости.
Поток жидкости. Под потоком жидкости подразумевается движение безразмерного множества отдельных частиц, которые движутся по своим траекториям. Как и в гидростатике, основной искомой величиной является величина гидростатического давления, а также значения скорости, расхода и т.п. при условии движения всех частиц жидкости.

Скорость течения потока. Под скорость движения потока жидкости подразумевается суммарное передвижение всех частиц потока в одном направлении. В связи представлением о скорости потока необходимо ввести ряд определений скорости.

Локальная скорость течения. Локальной скоростью движения жидкости является скорость движения безразмерно малой частицы жидкости.

Средней скоростью течения. Под средней скоростью движения потока жидкости подразумевается суммарное передвижение всех частиц потока в одном направлении, проходящее через площадку перпендикулярную векторам скорости. Локальная и средняя скорость движения потока жидкости связаны выражением: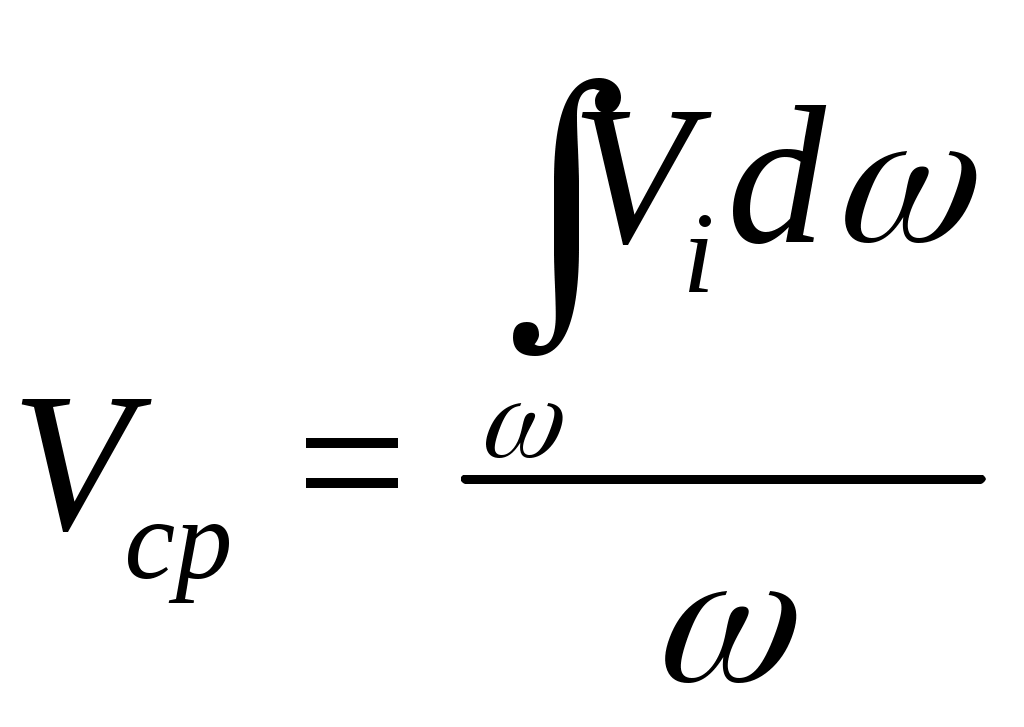
, (31)
где - локальная скорость; - площадь поперечного сечения движению потока.
Установившийся (стационарный) поток движение жидкости. Установившимся потоком движение жидкости является поток, скорость в котором не зависит от времени рис 2.2.6.


Рис. 2.2.6.
Переменный, установившийся (квазистационарный) поток движения жидкости. Квазистационарным установившимся потоком движения жидкости является поток, скорость в котором меняется в установленном порядке от времени, рис 2.2.8.



Рис. 2.2.7.
Неустановившийся (нестационарный) поток движение жидкости. Неустановившимся потоком движение жидкости является поток, скорость в котором зависит только от времени, рис 2.2.8.



Рис. 2.2.8.
Элементарная струйка. Понятие об элементарной струйке жидкости дает возможность рассматривать группу струек, движущихся совместно. Элементарна струйка (линяя тока) рис.2.2.9 может быть представлена как кривая, проходящая мгновенно совместно с такими же частицами, скорость которых направлены по касательной к этой кривой.

При этом установившееся движение можно представить как совокупность элементарных струек (линий тока), движущихся с равными скоростями частиц скользящими одна по другой. Линии тока в этом случае можно рассматривать как отдельные линии потока, к которым стремятся элементарные струйки при бесконечном уменьшении площадей их сечения. Такая совокупность движущихся струек образует поток жидкости.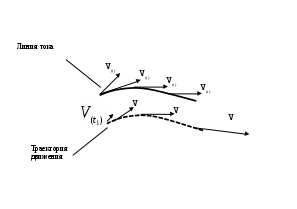


Рис.2.2.9.
Траектория движения частицы не является линией тока. В частном случае (стационарный режим движения) линия тока совпадает с траекторией и описывается функцией траектории.

Расход жидкости. Произведение площади элементарной струйку потока жидкости на величину локальной скорости движения U представляет некоторое количество жидкости. Это количество жидкости называется элементарным объемным расходом
. (32)
Определение расхода всего потока жидкости затрудняется не знанием закона распределения скоростей по сечению.

В этом случае можно записать:
(33)
Предполагая толкование средней скорости потока как выражение: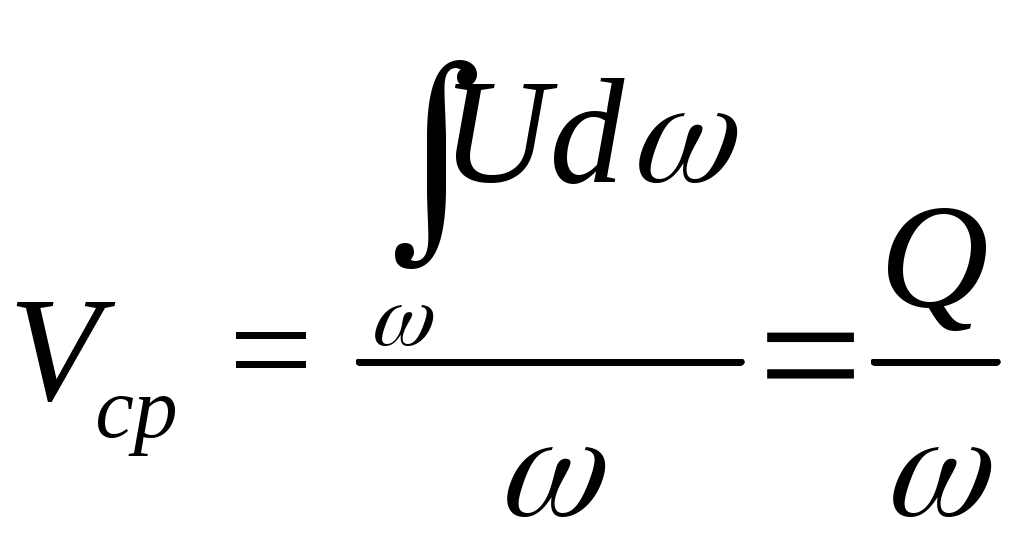
(34)
Исходя из выражения (34) можно записать:
(35)
В отдельных случаях секундный расход жидкости измеряют в весовых единицах, в кгс/сек. Такой элементарный расход называют весовым:
(36)
Смоченный периметр. Часть периметра поперечного сечения, образуемое твердыми стенками, входящее в контакт с потоком жидкости, называется смоченным периметром. Следовательно, при напорном движении смоченный периметр меньше полного периметра поперечного сечения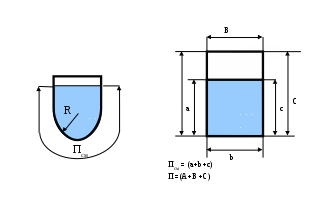


Рис.2.2.10.
Гидравлический радиус. Гидравлический радиус представляют собой отношение площади поперечного сечения потока к его смоченному периметру П_см:
, (37)
где - площадь поперечного сечения; П_см смоченный периметр.

Эквивалентный диаметр. Эквивалентный диаметр используется, как правило, в вентиляционной технике. Эквивалентный диаметр равен четырем гидравлическим радиусам.
(38)